Тамбовское областное государственное автономное профессиональное образовательное учреждение тогапоу Техникум отраслевых технологий
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Задача 66. На фирме «Канцлер» производятся только 3 товара: ручки, линейки и карандаши.
Определите норму инфляции для 2015 года. Решение: Норма инфляции = изменение уровня цен 2015 /уровень цен 2014 х 100% . СПК14 = 2 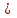 30 + 70 30 + 70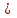 4 + 5 4 + 5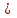 20 = 60+ 280 +100 =440. 20 = 60+ 280 +100 =440.СПК15 = 4 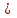 20 + 60 20 + 60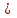 7 + 5 7 + 5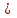 22 = 80 + 420 + 110 = 610. 22 = 80 + 420 + 110 = 610.Изменение уровня цен = 610 – 440 = 170. Норма инфляции = 170/ 440 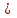 100% = 38,64%. 100% = 38,64%.Ответ: норма инфляции составила 38,64%. Задача 67. Имеются следующие данные: норма естественной безработицы – 6%; норма фактической безработицы – 8%; величина произведенного ВВП – 400 млн. ф. ст.; рассчитайте, чему равен потенциальный ВВП. Решение: Чтобы фактический ВВП достиг уровня потенциального, необходимо, чтобы норма безработицы снизилась до естественной нормы, т.е. до 6%, следовательно, на 2%. Таким образом, имеем: -2% = -0,4 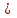 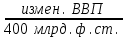 – 2,5%, откуда измен. ВВП = 30 млрд. ф. ст., а потенциальный ВВП = 400 млрд. ф. ст. + 30 млрд. ф.ст. = 430 млрд. ф. ст. – 2,5%, откуда измен. ВВП = 30 млрд. ф. ст., а потенциальный ВВП = 400 млрд. ф. ст. + 30 млрд. ф.ст. = 430 млрд. ф. ст.Задача 68. В 2002 г. среднемесячный размер пенсий в России равнялся 1379 р. Среднемесячная норма инфляции в этом же году равнялась 1,3%. В течение четырех месяцев размер пенсии не индексировался. Определите сумму реальных потерь пенсионера, получающего 1379 р., за четыре месяца; определите общую сумму потерь пенсионеров за четыре месяца, если их число в 2002 г. составило 30 млн. человек. Решение: Месячный индекс цен в 1995 г. равнялся: январь – 110, февраль – 121, март – 133,1, апрель – 146,41. (общий уровень цен в 1994 г. = 100). Таким образом, среднемесячная реальная пенсия изменялась следующим образом: январь – 168 182 р., февраль – 152893 р., март – 138993 р., апрель – 126357 р. Сумма потерь одного пенсионера в среднем составила за 4 месяца 153575р., а общая сумма потерь 30 млн. пенсионеров – свыше 4600 млрд. рублей. Задача 69. Согласно договору о найме квартиры ежемесячная квартплата устанавливается в соответствии с ожидаемой нормой инфляции 2% в месяц. В январе данного года квартплата была установлена в сумме 100 р. Фактическая норма инфляции оказалась 3% в месяц. Кто оказался в выигрыше — владелец квартиры или квартиросъемщик? Чему равен выигрыш одного и потеря другого? Решение: В соответствии с условиями о найме квартиры квартирная плата должна возрастать по месяцам следующим образом: январь – 100, февраль – 102, март – 104,04, апрель – 106,12 и т.д. В соответствии с фактической нормой инфляции индекс цен повышался следующим образом: январь – 100, февраль – 103, март – 106, 09, апрель – 109, 27. Таким образом, реальная квартирная плата изменялась следующим образом: Январь – 100. Февраль – 102/103 = 99,029. Март – 104,04/ 106, 09 = 98, 068. Апрель – 106,12/109, 27 = 97, 117. Если бы ожидаемая норма инфляции равнялась фактической, то реальная квартирная плата оставалась бы на уровне 100 р. Соответственно владелец квартиры недополучил реальную сумму: в январе – 0, в феврале – 0, 971 р., в марте – 1,932 р., в апреле – 2, 883 р. Задача 70. Рассчитайте: а) валовой доход; б) прибыль от обычной деятельности; в) чистую прибыль промышленного предприятия по данным: - выручка от реализации продукции (с НДС 18%) 2370 тыс. руб.; -расходы, относимые на себестоимость — 1520 тыс., в том числе расходы на оплату труда — 922 тыс. руб., -внереализационные расходы — 107 тыс. руб Решение: Валовой доход = (выручка от реализации продукции )- (расходы, относимые на себестоимость)= 2370-1520=850 Операционная прибыль = (валовая прибыль)- (операционные затраты)= 850-107=743. Чистая прибыль = Валовая прибыль — Сумма операционных затрат — Сумма налогов, пеней и штрафов, процентов по кредитам = 850-107-426,6-322,8=595,6 Задача 71. Оценить курс облигации сроком 5 лет с ежегодной выплатой купонов в размере 30% от номинала (с = 0,3): В момент эмиссии Спустя 1 год Спустя 2 года. Решение: Текущая процентная ставка составляет 25%. Годовой дисконтный множитель 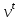 = 1/ (1+ 0,25) = 0,8 = 1/ (1+ 0,25) = 0,8Курс облигации: В момент эмиссии К (5)/100 = 1+(0,3/0,25-1)*(1- 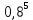 ) = 1,1345 ) = 1,1345Год спустя К (4) /100 = 1+(0,3/0,25-1)*(1- 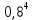 ) = 1,1181 ) = 1,1181Два года спустя К (3) /100 = 1+(0,3/0,25-1)*(1- 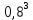 ) = 1,0976 ) = 1,0976Задача 72. Доля бракованной продукции в 1 партии изделий составила 1%, во 2 партии - 1,5%, а в третьей - 2%. Первая партия составляет 35% всей продукции, вторая - 40%. Определить средний процент бракованной продукции. Решение: По данным задачи составим таблицу.
Средний процент бракованной продукции определим по формуле средней арифметической взвешенной: Ответ: б) 1,45%. Задача 73. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и ответственного за дежурство. Сколько существует способов это сделать? Решение: Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а ответственным за дежурство – любой из оставшихся 28 студентов, т.е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и ответственного за дежурство равно N=n1n2n3=302928=24360. Задача 74. Рассчитать точку безубыточности и порог безубыточности производства. Определить уровень отпускной цены. Определить цену продукции при заданном объеме прибыли. Определить выручку от реализации. Исходные данные: Постоянные затраты на единицу продукции = 150 руб. Переменные затраты на единицу продукции = 250 руб. Рыночная цена = 400 руб. Спрос на продукцию = 1000 шт. Заданная сумма прибыли = 50 тыс. руб Решение: Расчет точки безубыточности предполагает расчет минимального объема производства, который дает возможность покрыть затраты. Эта величина рассчитывается как отношение общей суммы постоянных затрат на разницу между ценой и переменными затратами на единицу продукции: ТБ=150*1000/(400-250)=1000 ед. Порог безубыточности представляет собой минимальный объем производства в денежном измерении в рыночных ценах: ПР=1000*400=400000 руб. Уровень отпускной цены принимаем на уровне рыночной цены при заданном спросе на продукцию, т.е. 400 руб. Цену продукции при заданном объеме прибыли определяем, исходя из того, что выручка от реализации должна покрыть все затраты и обеспечить заданную сумму прибыли: Р=(150*1000+250*1000+50000)/1000=450 руб. Выручка от реализации составляет: В=450*1000=450000 руб. Задача 75. Пожаром 20 июня супермаркете «Виктория» были повреждены товары. На 1 июня в магазине имелось товара на 3500 тыс. руб. С 1 по 20 июня поступило товаров на 2800 тыс. рублей, сдано в банк выручки 3200 тыс. руб., сумма несданной выручки – 60 тыс. руб., естественная убыль составила 1,2 тыс. руб. После пожара был произведен учет спасенных товаров на сумму 2036,2 тыс. руб. Издержки обращения – 10%, торговая надбавка – 25%. Расходы по списанию и приведению товаров в порядок составили 8,0 тыс. руб. Страховая сумма составляет 70% от фактической стоимости товаров на момент заключения договора страхования. Исчислите ущерб страхователя и величину страхового возмещения. Решение: Определяем: 1) стоимость товара в универмаге на момент пожара = 3500 + 2800 – 3200 – 60 – 1,2 = 3038,8 тыс. руб.; 2) стоимость погибшего и уценки поврежденного имущества = 3038,8 – 2036,2 = 1002,6 тыс. руб.; 3) ущерб = стоимости погибшего и уценки поврежденного имущества – торговые надбавки + издержки обращения + расходы по спасанию и приведению имущества в порядок; где торговые надбавки и издержки обращения равны: Торговые надбавки = (стоимость погибшего и уценки поврежденного имущества*уровень надбавок в %)/ (100 + уровень торговых надбавок в %) Издержки обращения = (стоимость погибшего и уценки поврежденного имущества *уровень издержек в %)/100 Торговые надбавки = 10002,6*25 / (100+25)=200,52 тыс. руб. Издержки обращения = 10002,6*10 / 100=100,26 тыс. руб. Ущерб = 1002,6 – 200,52 + 100,26 + 8,6 = 910,94 тыс. руб. Величина страхового возмещения = 910,94*0,7 = 637,658 тыс. руб. Задача 76. Объект стоимостью 6 млн. рублей застрахован по одному договору тремя страховщиками: первым – на сумму 2,5 млн. руб., вторым на сумму 2 млн., третьим на сумму 1,5 млн. руб. Страховым случаем (произошел пожар) нанесен ущерб объекту в сумме 1,8 млн. руб. Определите размер выплаты страхователю каждым страховщиком. Решение: Первым: (1,8*2,5)/6 = 0,75 млн. руб. или 750 тыс. руб. Вторым: (1,8*2)/6 = 0,6 млн. руб. или 600 тыс. руб. Третьим: (1,8*1,5)/6 = 0,4 млн. руб. 450 тыс. руб. Задача 77. Выполните следующие расчеты по операциям с векселями: 1. Простой вексель выдается на сумму 800 тыс. руб., с уплатой в конце года. Какую сумму владелец получит, если он учтет вексель за 5 месяцев до срока погашения по простой учетной ставке 12% годовых? 2. Переводной вексель (тратта) выдается на сумму 2 млн. руб., срок его погашения – 2 года. Какова сумма дисконта при учете векселя по сложной учетной ставке, равной 18% годовых? Решение 1 ситуации: Находим стоимость векселя по формуле: P = S (1 – nd), где: S – выплачиваемая сумма денежных средств по векселю в момент погашения; n – количество периодов наращения; d – учетная ставка ( в долях от единицы). Поскольку в 1 ситуации учет будет исчисляться в месяцах, то d разделим на 12, т.е. 80000*(1 –5*0,12/12) = 760000 руб. Во второй ситуации находим стоимость векселя в настоящее время по формуле: P = S (1 – d)n P = 2000000*(1 – 0,18 )2 = 1344800 руб. Находим сумму дисконта как разницу между суммой векселя, выплачиваемой в момент его погашения и сегодняшней стоимостью векселя: 2000000 руб. – 1344800 руб. = 655200 руб. Задача 78. Инвестор приобрел акцию. Сумма дивидендов в первый год – 50$, а в последующие годы возрастает на 10$ ежегодно. Норма текущей доходности акции 15% в год. Определите текущую рыночную цену акции из условия работы с ней в течение 5 лет. Решение: 1) Определим сумму дивидендов в 2,3,4, 5 год. 2 год 50 + 10 = 60$ 3 год 60 + 10 = 70$ 4 год 70 + 10 = 80$ 4 год 80 + 10 = 90$ 2) Рыночная цена ∑ Дт/ (1+ I)n = 50/(1 + 0,15) + 60/(1 + 0,15)2 + 70/(1 + 0,15)3 + 80/(1 + 0,15)4 + 90/(1 + 0,15)5 = 225,36$, где: Дт – сумма дивидендов; I – ставка процента; n – число лет. Задача 79.Микроволновая печь ценой 2 тыс. руб. продается в кредит год под 10% годовых. Погасительные платежи вносятся через каждые три месяца. Определить размер разового погасительного платежа. Решение: Сумма, подлежащая погашению за весь срок кредита: S = P(1+in), где: Р – сегодняшняя стоимость платежей, S – сумма денежных средств, которая будет выплачена к концу срока, n – срок кредита в годах I – ставка %. S = 2(1 + 1*0,1) = 2,2 тыс. руб. Разовый погасительный платеж: q = S/nm, где: m – число платежей. q = 2,2/1*4 = 0,55 тыс. руб. или 550 руб. Задача 80. Кредит в сумме 10 тыс. $ выдан на шесть месяцев под 20% годовых (проценты простые). Погашение задолженности производится ежемесячными платежами. Составить план погашения задолженности. Решение: Наращенная сумма долга в конце периода составит: S = Р(1 + in) = 10(1 + 0,5*0,2) = 11 тыс. $, где: Р – сегодняшняя стоимость платежей, S – сумма денежных средств, которая будет выплачена к концу срока, n – срок кредита в годах, i – ставка %. Сумма начисленных процентов: I = Рin I = 10*0.5*0.2 = 1 тыс. $ Ежемесячные выплаты: q = S/nm, где: S – сумма денежных средств, которая будет выплачена к концу срока, m – число платежей, n – число лет. q = 11000/6 = 1833,33$ Найдем сумму порядковых номеров месяцев: 1 +2+3+4 + 5+6 = 21 Из первого платежа в счет уплаты процентов идет 6/21 общей суммы начисленных процентов: 6/21*1000 =285,71 $ Сумма, идущая на погашение основного долга, составляет: 1833,33 – 285,71 = 1547,62 руб. Из второго платежа в счет уплаты процентов идет 5/21 общей суммы начисленных процентов: 5/21* 1000 =238,09 $ Сумма, идущая на погашение долга: 1833,33 – 238,09 = 1595,24$ План погашения долга:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
