Тамбовское областное государственное автономное профессиональное образовательное учреждение тогапоу Техникум отраслевых технологий
 Скачать 0.54 Mb.
|
|
Задача 22. Определите границы изменения среднего значения признака в генеральной совокупности, если известно следующее её распределение, основанное на результатах повторного выборочного обследования:
Уровень доверительной вероятности определите самостоятельно. Решение Среднее значение признака по выборке: 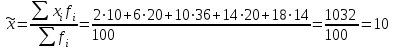 Выборочная дисперсия: 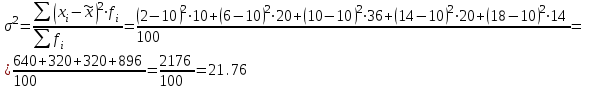 Вероятность ошибки установим – 0,954, соответственно уровень коэффициента доверия составит 2. 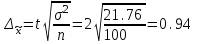 Установим границы изменения среднего значения признака в генеральной совокупности  Таким образом, с вероятностью 0,954 можно утверждать, что среднее значение признака в генеральной совокупности будет находиться в пределах от 9,06 до 10,94. Задача 23. В результате случайной повторной выборки в городе предполагается определить долю семей с числом детей три и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,27. Решение Необходимый объём выборки определим по формуле:  семейЧисленность выборки должна составлять 2700 семей. Задача 24. Проведено выборочное наблюдение партии однородной продукции для определения процента изделий высшего сорта. При механическом способе из партии готовых изделий в 20000 единиц было обследовано 800 единиц, из которых 640 изделий отнесены к высшему сорту. Определите с вероятностью 0,997 возможный процент изделий высшего сорта во всей партии. Решение В случае механического отбора предельная ошибка определяется по следующей формуле: 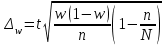 ,где t - коэффициент доверия t=3 при р = 0,997; N – численность генеральной совокупности; n- численность выборки; w – выборочная доля. Определяем выборочную долю w = 640/800 = 0.8 Рассчитываем предельную ошибку выборки  Устанавливаем границы генеральной доли изделий высшего сорта: Следовательно, генеральная доля находится в пределах: 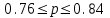 Задача 25. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:
Определить: - среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997; - долю рабочих предприятия, имеющих месячный доход 1400 руб. и выше, гарантируя результат с вероятностью 0,954; - необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 50 руб.; - необходимую численность выборки при определении доли рабочих с размером месячного дохода 1400 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 2 %. Решение Средний месячный доход по выборке 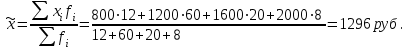 Определяем дисперсию выборочной средней 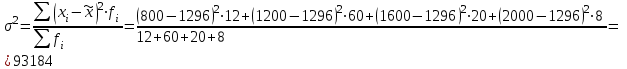 Предельная ошибка выборки при вероятности р=0,997 t=3 составит: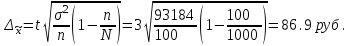 Доверительный интервал среднего размера месячного дохода работников предприятия  Следовательно, с вероятностью 0,997 можно утверждать, что среднемесячный размер дохода у работников данного предприятия находится в пределах от 1209,1 до 1382,9 руб. 2) Определим долю рабочих (w), имеющих размер месячного дохода 1400 руб. и выше: 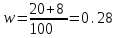 Предельная ошибка выборки при вероятности р=0,954 t=2 составит: 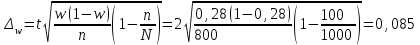 Устанавливаем доверительные интервалы для генеральной доли: 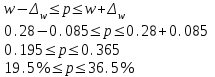 С вероятностью 0,954 можно гарантировать, что доля рабочих предприятия имеющих месячный доход 1400 руб. и выше, находится в пределах от 19,5 до 363,5 %. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле: 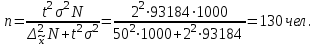 Необходимая численность выборки для определения доли рабочих, имеющих доход 1400 руб. и выше, определяется по формуле:  Задача 26. На основании выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем, объёме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется. Требуется определить численность выборки, если результаты выборки дать с точностью до 1 % и гарантировать это с вероятностью 0,95. Решение По условию задачи известны: 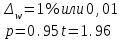 Так как значение w не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение w=0.5 Необходимая численность выборки составит: 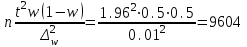 Следовательно, чтобы с заданной точностью определить долю частных писем в общем, объёме отправляемой корреспонденции необходимо в порядке случайной выборки отобрать 9604 письма. Задача 27. Имеются следующие данные о продаже легковых автомобилей в России:
Определить показатели динамики продажи легковых автомобилей от года к году и средние за весь анализируемый период: Решение: Решение задачи оформим таблицей:
Средний уровень интервального ряда динамики:  тыс. руб.Средний абсолютный прирост  тыс. руб.или 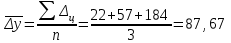 тыс. руб.Средний коэффициент роста: 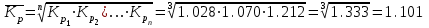 или 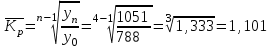 Средний темп роста 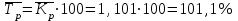 Средний темп прироста 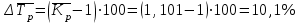 или 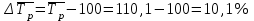 Средняя величина абсолютного значения 1 % прироста 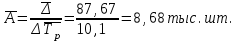 Задача 28. Имеются следующие данные о стоимости имущества предприятия (млн. руб.):
Определить абсолютное и относительное изменение среднегодовой стоимости имущества в 2010 г. по сравнению с 2008 и 2009 гг. Решение: Поскольку промежутки времени между датами равны, средний уровень моментного ряда динамики исчисляется по формуле:  ,где у1 и у n - уровни соответственно на начало и на конец периода, за который исчисляется средний уровень; n - число уровней ряда. 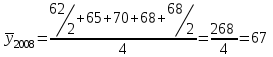 млн. руб.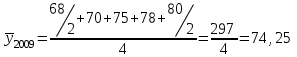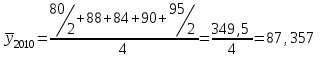 млн. руб. млн. руб.В 2010г. среднегодовая стоимость имущества предприятия возросла по сравнению с 2008г. на 20,375 млн. руб. (∆ = 87,375 - 67) или на 30,4% (Кр = 87,375 : 67 = 1,304), и по сравнению с 2009г. - на 13,125 млн. руб., или на 17,7% (13,125 : 74,25 ∙ 100) Задача 29. Имеются следующие данные о выпуске продукции предприятия по месяцам за год в сопоставимых ценах:
Решение Укрупним интервалы до трёх месяцев и рассчитаем суммарный и среднемесячный выпуск продукции по кварталам. Новые данные будут выглядеть следующим образом (табл. 20): Таблица 20 Данные о выпуске продукции после укрупнения интервалов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||