Организация и экономика фпрмации. Тема 7 Общая характеристика учетной политики аптечной организации
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
Корреляционно-регрессионный анализ, как общее понятие, включает в себя измерение тесноты связи, направление связи и установление аналитического выражения формы связи (уравнения регрессии). Данный метод содержит две свои составляющие части – корреляционный анализ и регрессионный анализ. Корреляционный анализ – выявление и оценка связи между случайными величинами, не находящимися в функциональной зависимости. То есть решается вопрос: существует ли связь между исследуемыми явлениями и насколько она сильна? Непременными условиями корреляционного анализа являются обеспечение репрезентативности статистических данных (репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана). Регрессионный анализ – это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами и оценка её адекватности. Регрессионный анализ используется для нахождения уравнения, которое связывает зависимую переменную с одной или несколькими независимыми переменными (независимые переменные иначе называют регрессорами). Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. Основная задача регрессионного анализа – установление формы и изучение зависимости между случайными величинами, решается вопрос: каков характер связи (прямая, обратная) между исследуемыми явлениями, а также строится и исследуется регрессионная модель. Регрессионный анализ используется для прогноза, анализа временных рядов, тестирования гипотез и выявления скрытых взаимосвязей в данных. 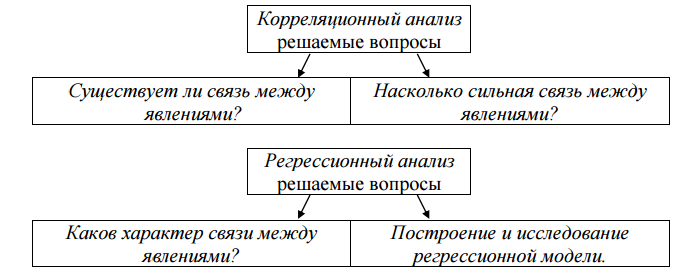 Наиболее простым и эффективным способом выявления взаимосвязей между явлениями, с которого начинается корреляционный анализ, является графический метод. Для этого на координатном поле наносят точки, соответствующие значениям изучаемых признаков X и Y. На оси абсцисс откладывают значения независимого признака Х, на оси ординат – зависимого признака Y. Совокупность точек образует корреляционное поле. По характеру расположения точек на корреляционном поле можно судить о направлении и силе связи. Если точки беспорядочно разбросаны по полю, то зависимость между переменными отсутствует; если точки образуют эллипс, то имеется прямая (или обратная) зависимость между исследуемыми признаками. 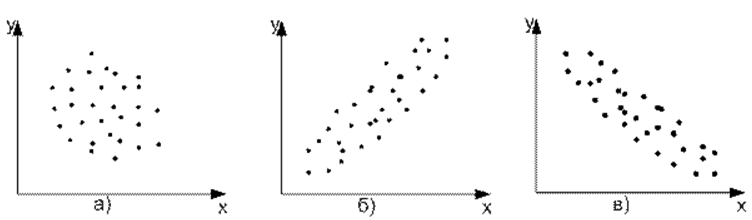 Корреляционное поле при отсутствии зависимости между признаками (а), при наличии прямой зависимости (б), при наличии обратной зависимости (в). Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от – 1 до + 1. 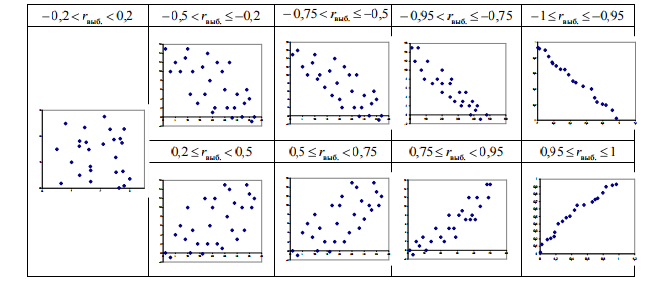 Если значение коэффициента корреляции находится в интервале от 0,6 до 0,6 , то говорят об очень слабой корреляционной зависимости или полной ее отсутствии. Если значение коэффициента корреляции лежит в интервале от 0,6 до 0,9, то говорят, что имеет место слабая корреляционная зависимость. Если значение коэффициента корреляции лежит в интервале от 0,9 до 1, то отмечается очень сильная корреляционная зависимость. Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами. Регрессионный анализсвоей целью имеет найти значение зависимой переменной, если величина независимой переменной (или независимых переменных) известна. Практически речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию регрессии, т.е. линию, по возможности, точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию). Теория массового обслуживания изучает системы, предназначенные для обслуживания массового потока требований случайного характера (случайными могут быть как моменты появления требований, так и затраты времени на их обслуживание). В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, покупка ЛС в аптеке и т.п. Теория массового обслуживания исследует на основе теории вероятностей математические методы количественной оценки процессов массового обслуживания. Целью исследований является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из нее, длительности ожидания и длины очередей. В теории массового обслуживания используются методы теории вероятностей и математической статистики. При этом зачастую требуются хронометражные наблюдения по обслуживанию потребителей. Целью анализа может быть определение вероятности отказа в предоставлении определенных услуг или обслуживании заявок. Типичным примером объектов теории массового обслуживания могут служить автоматические телефонные станции, на которые случайным образом поступают «требования» – вызовы абонентов, а «обслуживание» состоит в соединении абонентов с другими абонентами, поддержании связи во время разговора и т.д. Использование методов теории массового обслуживания позволяет организовать обслуживание, обеспечивающее заданное его качество. В теории массового обслуживания рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. Основной задачей теории массового обслуживания является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории массового обслуживания возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств. Теория массового обслуживания представляет значительный интерес для разработки оптимальных вариантов организации торговли медицинскими товарами и снабжения ими лечебных учреждений. Теория игр – это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы. Теория игр позволяет исследовать конфликтные ситуации и на основе этого разрабатывать рекомендации по наиболее рациональному образу действий каждого из участников в ходе конфликтной ситуации. Формализуя конфликтные ситуации математически, их можно представить, как игру двух, трех и более игроков, каждый из которых преследует цель максимизации своей выгоды, своего выигрыша за счет другого. Решения, получаемые с помощью теории игр, полезны при перспективном анализе возможных действий в условиях возможного противодействия конкурентов или неопределенности во внешней среде. Игровую схему можно придать многим ситуациям в экономике. Здесь выигрышем могут быть эффективность использования дефицитных ресурсов, производственных фондов, величина прибыли, себестоимость и т.д. Теория игр может использоваться и для выбора оптимального решения, например, при создании запасов сырья, материалов, полуфабрикатов. В данном случае противоборствуют две тенденции: увеличения запасов, в том числе и страховых, гарантирующих бесперебойную работу производства, и сокращения запасов, обеспечивающих минимизацию затрат на их хранение. Методы и рекомендации теории игр разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл. Для решения задач применяют алгебраические методы, основанные на системе линейных уравнений неравенств, итерационные методы, а также приведение задачи к системе дифференциальных уравнений. Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учтя лишь важнейшие факторы, существенно влияющие на ход конфликта. Теория массового обслуживания и математическая теория игр являются довольно сложными методами количественной оценки процессов массового обслуживания, оценки наивыгоднейших производственных решений и разработки системы хозяйственных экспериментов. В аптечной системе эти методы пока не нашли применения. Метод линейного программирования основан на решении линейных уравнений, когда зависимость между изучаемыми явлениями строго функциональная. Линейное программирование можно применить только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность. Экономические задачи, решаемые с помощью линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу – значит выбрать из всех допустимо возможных вариантов оптимальный. В аптечной системе методом линейного программирования можно решать задачи, связанные с рациональным размещением сельской аптечной сети с формированием оптимальных зон лекарственного обслуживания в сельской местности с распределением товарных фондов. Однако, большое количество расчетных действий, вызываемых многообразием факторов и их возможных комбинаций, требует обязательного применения счетно-вычислительной техники, в связи с чем область применения линейного программирования остается ограниченной. 4.8.2. ПЛАНИРОВАНИЕ РЕЦЕПТУРЫ АПТЕКИ Классификация рецептуры аптеки, ее значение Рецептура – это объем лекарственной помощи, оказанной населению по рецептам врачей и требованиям организаций здравоохранения. В зависимости от источника поступления общая рецептура делится на амбулаторную и стационарную, что представлено на рисунке 1. 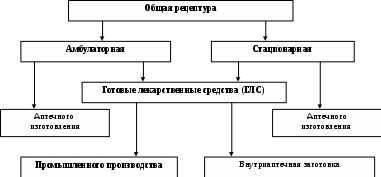 Рисунок 1 – Структура рецептуры аптек Амбулаторная рецептура характеризует объем лекарственной помощи, оказанной населению по рецептам врачей, в т.ч. по бесплатным и льготным рецептам. Стационарная рецептура характеризует объем лекарственной помощи, оказанной по требованиям организаций здравоохранения и других учреждений. Амбулаторная и стационарная рецептуры, в свою очередь, делятся на рецептуру аптечного изготовления (экстемпоральные лекарственные средства) и готовые лекарственные средства (ГЛС). Готовые лекарственные средства могут быть промышленного производства и внутриаптечного изготовления. Рецептура - один из важнейших показателей деятельности аптеки. Ее значение заключается в следующем: Выполнение плана по рецептуре влияет на выполнение плана товарооборота аптеки. Количество рецептов лежит в основе штатных нормативов для некоторых должностей фармацевтического персонала, таких как провизор-рецептар, провизор-аналитик, фармацевт-ассистент, что регламентируется приказом МЗ РБ № 565-А от 30.11.95 г. Количество рецептов врача на аптечное изготовление лекарственных средств, сложность прописей, особенности изготовления некоторых лекарственных форм определяют объем производственных функций аптеки. Объем рецептуры влияет на доходы аптеки: с одной стороны стоимость услуги за аптечное изготовление лекарственных средств включается в доходы аптеки, с другой стороны, дополнительные расходы, связанные с аптечным изготовлением лекарственных средств, увеличивают издержки обращения аптеки. Объем и характер рецептуры влияют на производительность труда фармацевтических работников, так как определяют трудоемкость процессов, связанных с изготовлением и реализацией лекарственных средств. Количество рецептов врача на аптечное изготовление лекарственных средств определяет необходимость наличия вспомогательных материалов (этикетки, пробки, капсулы, резиновые обхватки, сигнатуры, нитки, пергаментная, вощеная и оберточная бумага, моющие и дезинфицирующие средства и др.). В зависимости от стоимости лекарственных средств аптечного изготовления и внутриаптечных заготовок рассчитывается сумма естественной убыли лекарственных средств, спирта этилового, ваты. Удельный вес готовых лекарственных средств в рецептуре аптеки характеризует качество обслуживания населения, так как свидетельствует о том, какая часть посетителей, обратившихся в аптеку с рецептами, получила лекарственное средство сразу. Чем выше удельный вес готовых лекарственных средств в рецептуре аптеки, тем выше производительность труда, тем ниже трудоемкость производственных операций, тем ниже издержки обращения. 2. Факторы, влияющие на объем рецептуры На количество поступающих в аптеку рецептов врачей оказывают влияние следующие факторы: Численность и половозрастной состав обслуживаемого населения. Наличие амбулаторно-поликлинических учреждений в обслуживаемом районе. Численность врачей, ведущих амбулаторный прием пациентов, их профиль, доступность их для населения. Разветвление аптечной сети региона. Ассортимент лекарственных средств в самой аптеке, минимизация отказов в отпуске лекарственных средств по причине их отсутствия. Цены на лекарственные средства. Уровень материального благосостояния населения и, соответственно, его покупательская способность. Уровень заболеваемости населения, сезоны года. Эффективность информационной работы среди медицинского персонала. Сумма ассигнований, выделяемых из бюджета на бесплатное и льготное обеспечение пациентов лекарственными средствами и перевязочными материалами, на лекарственное обеспечение пациентов, получающих медицинскую помощь в стационарных условиях. Профиль и число мест (коечный фонд) в обслуживаемых стационарных организациях здравоохранения. Проведение профилактических мероприятий и др. 3. Методики планирования рецептуры Рецептура планируется в двух показателях: в натуральных (т.е. количество рецептов) и в денежных (стоимость рецептов). Стоимость отражают в разделе учета товарооборота. Планирование рецептуры осуществляется по ее составным частям: планируют амбулаторную рецептуру; планируют стационарную рецептуру; суммируют запланированные показатели и определяют общую рецептуру; находят удельный вес готовых лекарственных средств в общей рецептуре аптеки. Различают планирование рецептуры для уже функционирующих аптек и для вновь открываемых. 3.1. Планирование амбулаторной рецептуры для функционирующих аптек Функционирующая аптека располагает отчетными данными, которые являются основой для разработки плана. Существует несколько вариантов планирования. 1-й вариант планирования – метод динамических показателей (динамических рядов) – основан на общей методике анализа отчетных данных за ряд лет (3-4 года), предшествующих планированию. При этом действуют по следующей схеме: Составляют аналитическую таблицу, т.е. выписывают отчетные данные о количестве рецептов за 3-4 предшествующих периода. Так как на амбулаторную рецептуру значительное влияние оказывают сезоны года, для анализа нужно использовать отчетные данные 4-го и 1-го кварталов предплановых лет: они сходны по объему и характеру заболеваний. Например, имеются следующие отчетные данные по амбулаторной рецептуре за ряд лет:
Определяют динамику изменения показателя (увеличение, уменьшение количества рецептов, или показатель остаётся без изменений). Если тенденции изменения показателя не наблюдается, плановый показатель определяют как среднее арифметическое значение по отчетным данным. При наличии тенденции изменения показателя определяют цепные темпы роста или снижения показателя за каждый анализируемый период. |
