Теория и технология производства стали 1. Учебник для вузов. М. Мир, ООО Издательство act

• Название: Учебник для вузов. М. Мир, ООО Издательство act
• Анкор: Теория и технология производства стали 1.doc
• Дата: 22.04.2017
• Размер: 7.23 Mb.
• Имя файла: Теория и технология производства стали 1.doc
• Тип: Учебник; #5208
• страница: 13 из 88

8.1.2. Растворы. В сталеплавильной ванне участвующие в реакциях компо­ненты находятся в виде раствора в ме­талле (железе) и шлаке.

Раствором называют однородную смесь, состоящую из двух или больше­го числа веществ, состав которой в из­вестных пределах может непрерывно изменяться (однородными являются и химические соединения, однако их состав не может изменяться непре­рывно, так как они подчиняются зако­нам постоянства состава и кратных от­ношений).

При рассмотрении растворов вооб­ще и растворов, встречающихся в ста­леплавильной практике, в частности следует учитывать химическое и физи­ческое взаимодействия компонентов раствора. В одних случаях при образо­вании раствора никаких химических реакций не происходит, имеет место просто разбавление одного компонента другим; в других случаях одновремен­но с разбавлением происходит хими­ческое взаимодействие растворителя и растворенного вещества. При этом выделяется (или поглощается) тепло, что важно учитывать на практике. На­пример, при образовании раствора кремния в железе выделяется значи­тельное количество тепла. Это учиты­вается, например, при производстве кремнистой стали (динамной, транс­форматорной, ЗОХГС и т. п.). Плавку можно организовать таким образом, что перед выпуском металла богатые кремнием ферросплавы в твердом виде можно загружать в ковш без опа­сения переохлаждения плавки.

Вещество, переходя в раствор, ста­новясь компонентом раствора, теряет свою индивидуальность. Значение термодинамических функций для про­цессов (реакций), происходящих меж­ду веществами, находящимися в ра­створе, существенно отличается от та­ковых для реакций между чистыми веществами. Например, значения ΔG° для реакции окисления углерода, ра­створенного в металле, кислородом, находящимся в газообразном состоя­нии, или кислородом, растворенным в металле, различны:

1/20₂ + [С] = СО_Г,

ΔG° = -142 000 -40,79 Т;

[О] + [С] = СО_Г, ΔG⁰= -25 000 -37,9 Т.

Взаимодействие частиц растворите­ля и растворенного вещества может быть различным. Количественной ха­рактеристикой, учитывающей как кон­центрацию данного компонента в ра­створе, так и его взаимодействие с ра­створителем (или вообще с другими компонентами раствора), является ве­личина, называемая активностью дан­ного компонента в данном растворе. Смысл понятия активность может быть ясен из следующего. Между лю­бой жидкостью и парами этой жидко­сти устанавливается определенное рав­новесие (зависящее от температуры). Если в жидкости растворить какой-то другой компонент, то давление пара этой жидкости изменится. Значение подобного изменения широко исполь­зуют в термодинамических расчетах. Чтобы результаты расчетов можно было сравнивать, необходимо выбрать стандартное состояние, которое явля­ется единицей сравнения. В качестве стандартного состояния можно выб­рать любое состояние вещества. Обыч­но в качестве стандартного состояния выбирают либо чистое вещество, либо его однопроцентный раствор.

Если р — давление пара компонен­та, находящегося в растворе, а р° — давление пара компонента в стандарт­ном состоянии, то соотношение р/р° принято называть активностью данно­го компонента и обозначать а, или р/р° = а. Активность вещества в стан­дартном состоянии принимают рав­ной единице.

Для термодинамических расчетов активность представляет собой вспо­могательную расчетную величину, которая характеризует степень связанно­сти молекул, атомов или ионов иссле­дуемого компонента. При образова­нии данным компонентом в растворе каких-либо соединений его актив­ность понижается и, наоборот, актив­ность возрастает при уменьшении сил взаимодействия между частицами ра­створителя и растворенного вещества. Теоретически можно представить слу­чай, когда взаимодействие частиц ра­створителя и растворенного вещества равно взаимодействию частиц раство­рителя или чистого растворенного ве­щества. В этом случае при уменьше­нии концентрации в растворе одного из этих двух компонентов давление пара этого компонента над раствором умень­шается пропорционально уменьше­нию его концентрации в растворе, т. е. р = р°х, где х — мольная или атомная доля данного вещества в растворе. Это соотношение известно как закон Рау­ля, согласно которому давление пара каждого из компонентов раствора прямо пропорционально мольной доле данного компонента. В рассмат­риваемом случае (р = р°х; а = х) актив­ность численно равна мольной доле компонента. Такой раствор принято называть идеальным.

Для реальных растворов закон Рау­ля не всегда соблюдается. Наблюдае­мые отклонения от закона Рауля помо­гают установить природу образования тех или иных растворов. Представим себе раствор, состоящий из компонен­тов А и В. Частицы А и Л каким-то обра­зом взаимодействуют между собой. Можно принять, что имеются какие-то силы F_A._Aвзаимодействия частиц .А между собой, силы F_B._Bвзаимодей­ствия частиц В между собой и силы F_A._Bвзаимодействия частиц А и В.

При этом возможны следующие случаи.

1. Силы взаимодействия частиц А и В равны: F_A._A = F_A__B = F_B._B. В этом слу­чае активности компонентов А и В равны их мольной доле (активности изменяются по мере разбавления ра­створа): а_А = х_Аи а_в = х_в. Это идеаль­ный раствор.

2. Силы взаимодействия между ча­стицами Аи В меньше сил взаимодей­ствия между частицами А—А и В—В, т. е. F_A._A > F_A._B < F_B._B, ассоциированные молекулы А—В разъединяются; число молекул (частиц, комплексов) в растворе становится больше их числа в чистых компонентах. Практически наблюдается расширение системы (ΔV> 0), а также поглощение теплоты ( >0), которая затрачивается на разъединение ассоциированных мо­лекул в чистых компонентах. Вслед­ствие увеличения числа частиц в ра­створе парциальные давления и об­щее давление пара больше, чем в случае р_А =р°_Ах_А ир = р_А + р_в. Это по­ложительное отклонение от закона Рауля.

3. F_A__A < F_A__B > F_B__B, т. е. различные молекулы стремятся ко взаимодей­ствию типа притяжения (комплексо-образование, образование диполей и т. п.). В этом случае образование ра­створа сопровождается выделением теплоты (ΔН<0) и уменьшением объема (Δ V<0). Уменьшение числа частиц в растворе по сравнению с их числом в чистых растворителях при­водит к уменьшению парциальных давлений пара компонентов и обще­го давления пара системы. Это отри­цательное отклонение от закона Рау­ля. Характерным примером отрица­тельного отклонения от закона Рауля может служить раствор кремния в железе (рис. 8.1, а). Вид эксперимен­тально полученной кривой свиде­тельствует о том, что силы взаимо­действия кремния с железом F_Si._Fe много больше сил .F_si__si и F_Fe-_Fe. , т.е. F_Si-Si « F_Si-_Fe »F _Fe-Fe-

Отрицательным отклонением от за­кона Рауля характеризуются также ра­створы в железе таких компонентов, как алюминий, ванадий, титан. Если рассмотреть диаграммы состояния этих сплавов, то окажется, что в этих сплавах при охлаждении образуются химические соединения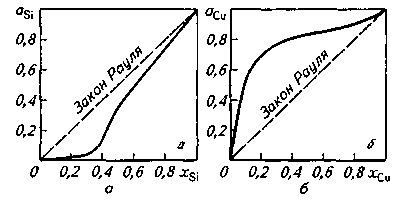



Рис. 8.1. Активность при 1873 К кремния (а) и меди (б) в жидких сплавах с железом
железа и ра­створенного компонента. Однако час­то нас интересует не столько характер этих связей, сколько сам факт того, что какие-то связи имеются, значит, ак­тивность данного компонента в резуль­тате наличия этих связей уменьшается.

Примером положительного откло­нения от закона Рауля (тенденция к от­талкиванию молекул растворенного компонента) может служить раствор меди в железе (рис. 8.1, б). При силь­ных положительных отклонениях от закона Рауля наблюдается расслоение на две несмешивающиеся жидкости (системы Fe-Ag, Fe-Pb), что также при­ходится учитывать на практике. На­пример, для улучшения обрабатывае­мости, полируемости и других свойств некоторых стальных изделий в сталь необходимо вводить свинец. В связи с трудностью образования однородного раствора свинца в железе применяют специальные, иногда дорогостоящие технологические приемы и получают сталь, содержащую необходимое коли­чество равномерно распределенного по массе металла свинца.

На практике чаще приходится иметь дело со сложными растворами (например, в железе одновременно ра­створены и кремний, и марганец, и уг­лерод и т. д.). Влияние «третьего» ком­понента может быть различным. Так, например, такие примеси, как марга­нец или хром, образуют с железом ра­створ, близкий к идеальному; если же в железе имеется растворенный угле­род, то при растворении марганца или хрома имело место отрицательное от­клонение от закона Рауля.

Большинство компонентов, встре­чающихся в металлургической прак­тике, образует с железом растворы, да­лекие от идеальных. Соотношения между составом и свойствами боль­шинства реальных растворов очень сложны и не всегда ясны. Положение облегчается тем, что обычно техноло­ги имеют дело с растворами, содержа­щими небольшие количества (часто < 1 %) других компонентов. При уменьшении концентрации раство­ренного вещества свойства реального раствора приближаются к свойствам идеального. Такие растворы принято называть бесконечно разбавленными или просто разбавленными. В этих слу­чаях принято использовать закон Ген­ри, согласно которому в разбавленном растворе давление пара растворенного вещества pjпрямо пропорционально его концентрации Сj, т.е. pj = rCj, где r—коэффициент (константа Генри). Обычно реальные растворы подчиня­ются закону Генри при изменении концентрации в интервале от долей процента до нескольких процентов¹.

Для достаточно сильно разбавлен­ного раствора можно принять актив­ность равной концентрации: aj= Сj, или aj — Xj. При повышении концент­рации растворенного компонента приходится вводить вспомогательную величину аj = jXj. Величина j, называ­емая коэффициентом активности, ха­рактеризует степень отклонения свойств рассматриваемого компонента в данном растворе от его свойств в идеальном растворе. Для идеальных растворов = 1. К таким растворам близки растворы никеля, кобальта, марганца, хрома, молибдена в железе.

Для ряда компонентов процесс ра­створения в железе сопровождается выделением (или поглощением) тепла (ΔН #0), а энтропия при растворении изменяется так же, как и в идеальных растворах, — только вследствие изме­нения концентрации ΔS° = — Rlnx. Это справедливо для растворов кремния, алюминия, меди в железе (такие ра­створы иногда называют регулярны­ми). Для многих растворов прихо­дится учитывать изменение энтро­пии не только в зависимости от концентрации, но и вследствие взаи­модействия вещества с растворите­лем ΔS°=—Rlnx+ΔS⁰ _вз.

К ним отно­сятся, например, растворы в железе углерода, серы (подобные растворы иногда называют реальными). Уравне­ния изменения энергии Гиббса при растворении ряда элементов в жидкой стали в числовом виде приведены в табл. 8.2. Для обозначения коэффици­ентов активности обычно используют символ или f. Буквой у обозначают коэффициент активности при исполь­зовании соотношения aj=jxj, т. е. когда концентрация выражена в моль­ных долях (компонента j). При выра­жении массовой концентрации в про­центах для обозначения чаще исполь­зуют букву f. В реальных условиях величина коэффициента активности компонента в растворе зависит от вза­имодействия растворенных в металле других компонентов. Для определения характера изменения коэффициента активности при изменении концент­рации компонентов расплава обычно используют соотношения, предложен­ные К. Вагнером. Если за стандартное состояние принят чистый компонент i, то при наличии в растворе кроме i других компонентов с мольными до­лями a, b, ...,j

Inyi =ln⁰ _i +ⁱ_i i+^a_i а+^b_i Ь+...+^j_ij,

где ⁱ_i, ^a_i, ^b_i,... ^j_i, —параметры взаимодей­ствия;


Таблица 8.2. Изменение энергии Гиббса

при образовании 1%-ного раствора ряда

элементов в жидком железе

Растворен­ный элемент	Yl873K	ДС° = ДД° -	ГдУ, Дж
А1	0,049	-62800 -	23,85 Т
В	0,040	-73200 -	12,30 Т
С	0,57	22600 -	42,26 Т
Са	2270	16200 -	58,58 Т
Со	1,07	1400 -	38,91 Т
Сг	1,0	—	37,66 Т
Сu	8,6	47200 -	46,65 Т
1/2H2(г) Мn	1,3	36500 + 5500 -	30,46 Т 39,12 Т
Мо	1,0	-	42,80 Т
1/2N2(r) Ni	0,66	10500 + -18000 -	20,38 Т 32,63 Т
1/2O2(г) 1/2P2 Pb	850	-117000 - -140200 -212500 -	2,89 Т 9,62 Т 106,27 Т
1/2S2(r) Si	0,0013	-72000 – -131800 -	10,25 Т 17,32 Т
Ti	0,037	-69500 -	27,28 Т
V	0,18	-42300 -	29,20 Т
W	1,0	—	48,12 Т
Zr	0,022	-80300 -	31,38 Т

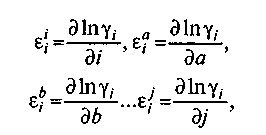т. е. параметр взаимодействия 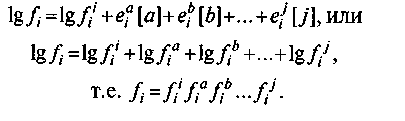ⁱ_i пока­зывает, как изменяется коэффициент активности _I при изменении мольной доли i; параметр ^a_i — как изменяется _I при изменении мольной доли ком­понента а и т. д. Для удобства расчетов параметры взаимодействия чаще оп­ределяют, принимая за стандартное состояние 1%-ный (по массе) идеаль­ный разбавленный раствор компонен­та i. В этом случае параметр взаимо­действия обозначают буквой е (а ко­эффициент активности — буквой f):



Если компонент а увеличивает ве­личину fi, этому соответствует ^a_i>0 (т. е. параметр взаимодействия имеет знак «плюс»). Если компонент Ь уменьшает f_iэтому соответствует е^b_i<0 (т. е. параметр взаимодействия имеет знак «минус»). Это означает, что компонент а взаимодействует с железом сильнее, чем компонент i, а компонент bслабее. Значения неко­торых параметров взаимодействия приведены в табл. 8.3.