тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 24 из 50

Задача 7.1. По данным табл. 7.3 проанализируем вариацию урожай- ности озимой пшеницы в области, для чего рассчитаем следующие по- казатели:

1. 
   размах вариации;
   
2. 
   среднее линейное отклонение;
   
3. 
   дисперсию;
   
4. 
   среднее квадратическое отклонение;
   
5. 
   коэффициент вариации.
   

Решение.

Размахвариации(R) характеризует общий диапазон колебаний зна- чений группировочного признака и рассчитывается по формуле

R= X_max – X_min = 31 – 15 = 16 ц/га.

Составим табл. 7.4, в которой покажем расчет показателей вариации.

116_•глава 7. ПОказатели вариации

Распределение сельскохозяйственных предприятий области по урожайности озимой пшеницы

Таблица 7.3

Группы предприятий по урожайности, ц/га	Количество предприятий, ед.
15—19	4
19—23	8
23—27	13
27—31	5
Итого	30

Информация об урожайности озимой пшеницы в табл. 7.3 пред- ставлена в форме интервального ряда. Поэтому в качестве значений признака (Х) возьмем середины интервалов в каждой группе.

Середина интервала (Х) для первой группы: (15 + 19) : 2 = 17 ц/га, для второй группы: (19 + 23) : 2 = 21 ц/га и т.д., (см. графу 2 табл. 7.4). Среднеелинейноеотклонениехарактеризует среднее отклонение зна- чений группировочного признака у отдельных единиц совокупности

от средней величины и рассчитывается по формуле

_{l }XXf <sub>,

</sub> f

где Х — значение группировочного признака у отдельных единиц совокупности;

^Х— средняя урожайность пшеницы по совокупности в целом (по области);

f— количество единиц в группе (количество предприятий).

Таблица 7.4

Методика расчета показателей вариации

Урожайность, ц/га	Количество предприятий f, ед.	X	X f	X Х	X Хf	(X Х)2 f
А	1	2	3	4	5	6
15—19	4	17	68	–6,5	26,0	169,00
19—23	8	21	168	–2,5	20,0	50,00
23—27	13	25	325	+1,5	19,5	29,00
27—31	5	29	145	+5,5	27,5	151,25
Итого:	30	Х	706	Х	93,0	399,50

Рассчитаем среднююурожайностьпшеницы по формуле

_Х ^Xf_ ^{1742182513295} _ ⁷⁰⁶ <sub> 23,5 ц/га.

</sub> f^{4  8  13  5 30}

7.1. вариация признака. Показатели вариации_•117

Промежуточные расчеты показаны в графе 3 табл. 7.4.

Вывод. В области с каждого гектара посевной площади собрали в среднем по 23,5 ц озимой пшеницы.

Проверка: 17 < 23,5 < 29.

Среднеелинейноеотклонениеисчислим по формуле

_{l }XXf <sub>

</sub> f

_ 1723,542123,582523,5132923,55 _

4  8  13  5

 ^93,0  3,1 ц/га.

30

Промежуточные расчеты отражены в графах 4 и 5 табл. 7.4.

Вывод. Урожайность озимой пшеницы в отдельных сельскохозяй- ственных предприятиях области отклоняется от средней урожайности по области (23,5 ц/га) в среднем на 3,1 ц/га.

Среднееквадратическоеотклонение() характеризует среднее от- клонение значений группировочного признака у отдельных единиц совокупности от средней величины и рассчитывается на базе диспер- сии (²).

Произведем расчет дисперсии(среднего квадрата отклонений):

_(X X)² f

399,50

²    13,32.

_ f³⁰

Единиц измерения дисперсия не имеет. Промежуточные расчеты показаны в графе 6 табл. 7.4.

Произведем расчет среднегоквадратическогоотклонения: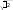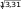

    3,6 ц/га.

Вывод. Урожайность озимой пшеницы в отдельных сельскохозяй- ственных предприятиях области отклоняется от средней урожайности по области в среднем (среднее квадратическое отклонение) на 3,6 ц/га.

Коэффициент вариации () характеризует относительное (в %) от- клонение значений группировочного признака у отдельных единиц совокупности от средней величины и рассчитывается по формуле

  ^ 100% 

X

^3,6 100%  15,3%.

23,5

118_•глава 7. ПОказатели вариации

Вывод. Урожайность озимой пшеницы в отдельных сельскохозяй- ственных предприятиях области отклоняется от средней урожайности по области в среднем на 15,3%.

Исчисленный коэффициент вариации  = 15,3% меньше 33,3% (критерия однородности совокупности), следовательно, вариация уро- жайности считается незначительной, а сельскохозяйственные предпри- ятия области по урожайности озимой пшеницы достаточно однородны.
Показатели альтернативного признака

На практике встречаются признаки, принимающие только два вза- имоисключающих значения. Например, состояние в браке имеет два значения: состоит в браке или не состоит в браке.

Формулы расчета среднего значения и дисперсии таких статисти- ческих признаков отражены в табл. 7.5.

Таблица 7.5

Показатели альтернативного признака

Показатель	Содержание показателя или формула расчета
Альтер- нативный признак	Это качественный признак, имеющий только два взаимо- исключающих значения. Наличие признака условно обозначают единицей «1», отсут- ствие признака — «0». Например, годная продукция (1), негодная (бракованная) про- дукция (0); состоит в браке (1), не состоит в браке (0)
Среднее значение альтерна- тивного признака	x (1p)(0q)  p, p q где p— доля единиц совокупности, обладающих признаком; q — доля единиц совокупности, не обладающих признаком (q = 1 – p). Средняя величина альтернативного признака равна доле еди- ниц, обладающих данным признаком или по-другому — сред- нее значение доли (p) равно самой доле
Дисперсия альтерна- тивного признака	2  (1 p)2  p (0  p)2  q    p qpq p(1 p). Предельное значение вариации альтернативного признака (при p = q = 0,5) равно 0,25

Правило сложения дисперсий

Дисперсия, исчисленная по совокупности в целом, не дает возмож- ность оценить влияние отдельных факторов на вариацию результатив-

7.1. вариация признака. Показатели вариации_•119 ного признака. Поэтому для изучения взаимосвязи между явлениями можно произвести аналитическую группировку, а затем с помощью

показателей вариации изучить связь, существующую между результа- тивным показателем и признаками-факторами (глава 3).

В этом случае кроме общей дисперсии (дисперсии для всей сово- купности в целом) можно рассчитать дисперсию для каждой группы отдельно, т.е. внутригрупповые дисперсии и среднюю из внутригруп- повых дисперсий (табл. 7.6).

Таблица 7.6

Правило сложения дисперсий

Показатель	Содержание показателя и формула расчета
Общая дис- персия	Характеризует вариацию признака во всей совокупности под влиянием всех факторов (x x0 )2 f 2   , 0 f где x0 — общая средняя арифметическая для всей изучаемой совокупности
Межгруппо- вая диспер- сия	Характеризует вариацию признака, обусловленную влиянием признака-фактора, положенного в основу группировки. Из- меряет колеблемость групповых средних вокруг общей сред- ней (систематическая вариация) (xi x0 )2 fi 2   , fi где xi— средняя величина по i-й группе; fi— количество единиц в i-й группе
Внутригруп- повая дис- персия	Измеряет вариацию признака внутри i-й группы под влия- нием всех факторов, кроме фактора, положенного в основу группировки (случайная вариация) (x xi)2 f 2   if
Средняя из внутри- групповых дисперсий	Характеризует вариацию признака под влиянием неучтенных факторов в среднем по всей совокупности 2  ifi, 2  fi где 2 — дисперсия по i-й группе i

120_•глава 7. ПОказатели вариации

Окончание

Показатель	Содержание показателя и формула расчета
Правило сложения дисперсий	2  2  2. i Позволяет рассчитать любую дисперсию, зная две других. Позволяет определить часть (долю) общей дисперсии, фор- мирующейся под влиянием признака-фактора, положенного в основу группировки

Дисперсия, как и средняя арифметическая величина, имеет опре- деленные свойства (табл. 7.7).

Таблица 7.7