тест по статистике. Гладун И. В_Статистика СКАН. Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо

• Название: Учебника для использования в учебном процессе образовательных учреждений, реализующих программы спо
• Анкор: тест по статистике
• Дата: 27.09.2022
• Размер: 1.13 Mb.
• Имя файла: Гладун И. В_Статистика СКАН.docx
• Тип: Учебник; #699128
• страница: 25 из 50

Свойства дисперсии

Свойство дисперсии	Формула расчета
1. Дисперсия постоянной величины равна нулю	2(a) = 0, где a— постоянная величина
2. Дисперсия не меняется, если всеварианты увеличить или уменьшить на одно и то же число a	2(a+ x) = 2(x); 2(a– x) = 2(x)
3. Если все варианты умножить на число a, дисперсия увеличится в a2 раз, т.е. постоян- ный множитель выносится за знак диспер- сии возведенным квадрат	2(a x)  a22(x)
4. Дисперсия от средней меньше, чем сред- ний квадрат отклонения от любого числа x0 на величину x. Это свойство минимально- сти дисперсии от средней	(X X)2 f   2(x)  (x0  x)2 f

Свойства дисперсии позволяют максимально упростить расчеты в случае вариационного ряда с равными интервалами


Расчет дисперсии способом моментов

Свойства дисперсии позволяют упростить ее расчеты, особенно для дискретных вариационных рядов и интервальных вариационных рядов с равными интервалами. Проиллюстрируем это на примере.

Пример 1. В главе 6, примере 1 была исчислена средняя арифметическая величина (средний стаж работы) упрощенным способом. Воспользуемся дан- ными этого примера для расчета дисперсии способом моментов (табл. 7.8).

Решение. Из предыдущих расчетов возьмем следующие показатели:

х₀ = 12,5; h= 5; ^{x 12 лет.}

1. 
   вариация признака. Показатели вариации_•121
   

Таблица 7.8

Расчет дисперсии способом моментов

Стаж рабочих, лет	Середина интервала x	Количество ра- бочих, человек f	x  xx0 h	x' f	(x')2f
А	1	2	3	4	5
До 5 [0—5]	2,5	9	–2	–18	36
5—10	7,5	29	–1	–29	29
10—15	12,5	32	0	0	0
15—20	17,5	23	1	23	23
20 и больше [20—25]	22,5	7	2	14	28
Итого:	Х	100	Х	–10	116

Дисперсию признака будем исчислять по формуле (см. табл. 7.1):




²  X²  X²,

т.е. дисперсия равна среднему квадрату минус квадрат средней.

Если в качестве значения осредняемого признака (x) взять преобразован-

ные варианты ^{ x  xx0 ,} то формула дисперсии с учетом свойств диспер-

_ _h_

сии будет исчисляться так:

^_^ _(x)²  f^{ }_

²  _  x² _h²

или

_^ ^{ f} _

²  h^{2 }_(x)² x^{2 }_.

Рассчитаем недостающие показатели:

x  ^xf 0,1;

_ f

(x)²  f (0,1)² 100  1;

_(x)²  f₁₁₆

(x)²    1,16;

_ f100

²  h^{2 }_(x)² x^{2 }_  5²(1,16 1)  4;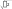

    2 года.

Вывод. Стаж работы отдельных рабочих предприятия отклоняется от среднего рабочего стажа по предприятию в среднем на два года; средний стаж находится в пределах от 10 до 14 лет ^{(12  2  x  12  2).}

122_•глава 7. ПОказатели вариации

2. 
   Структурные средние
   

В процессе анализа вариации признака исчисляют структурные средние: моду, медиану, квартили, делили, перцентили (табл. 7.9), кото- рые несут дополнительную информацию о распределении единиц со- вокупности. Например, в случае, когда невозможно рассчитать сред- нюю арифметическую величину, ее заменяют модой.

Таблица 7.9

Структурные характеристики ряда распределения

Наиме- нование показателя	Формула расчета в интервальном вариационном ряду
Мода	Это значение признака, которое чаще всего встречается в сово- купности M x hfMO fMO1 , 0 0 f f f f MO MO1 MO MO1 где x0 — нижняя граница модального интервала; h— величина модального интервала; fMO — частота модального интервала; fMO—1 — частота предмодального интервала; fMO+1 — частота послемодального интервала. Данная формула применяется для вариационных рядов с рав- нымиинтервалами
Медиана	Это значение признака, которое делит вариационный ряд по сумме частот на две равные части. Положение медианы: N n1, Me 2 где n— количество единиц в совокупности. Me  x h0,5fSMe1 , 0 f Me где x0 — нижняя граница медианного интервала; h— величина медианного интервала; SMe—1 — накопленная (кумулятивная) частота предмедианного интервала; fMe — частота медианного интервала
Квартили	Это значения признака, которые делят вариационный ряд по сумме частот на четыре равные части. Квартилей три (Q1, Q2 = Me, Q3)

2. 
   структурные средние_•123
   

Окончание

Наиме- нование показателя	Формула расчета в интервальном вариационном ряду
	Положение квартилей: N n1; N 2  n1; N 3  n1 ; Q1 4 Q2 4 Q3 4 Q x hNQSQ1 , 0 f Q где x0 — нижняя граница интервала, в котором находится квартиль; h — величина квартильного интервала (интервала, в котором находится квартиль); SQ—1 — накопленная частота интервала, предшествующая тому, в котором находится квартиль (предквартильного интервала); fQ— частота квартильного интервала (частота интервала, в ко- тором находится квартиль)
Децили	Это значения признака, которые делят вариационный ряд по сумме частот на десять равных частей. Децилей девять (D1, D2, …, D9). Положение децилей: N n1; N 2  n1; N 9  n1 ; D1 10 D2 10 D9 10 D x hNDSD1 , 0 f D где x0 — нижняя граница интервала, в котором находится де- циль (децильного интервала); h— величина децильного интервала; SD—1 — накопленная частота интервала, предшествующая тому, в котором находится дециль (преддецильный интервал); fD— частота интервала, в котором находится дециль
Перцен- тили	Это значения признака, которые делят вариационный ряд по сумме частот на 100 равных частей

В экономической практике исчисляют коэффициент децильной дифференциации, который показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень при- знака, больше наибольшего уровня признака из 10% единиц совокуп- ности, имеющих наименьший уровень признака:

K_D
где D₉ — девятая дециль;

D₁ — первая дециль.

 ^D9,

D₁

124_•глава 7. ПОказатели вариации

Дополнительно исчисляют коэффициентфондовойдифференциации:




_K ^xmax_,

Ф _x

min

где ^xmax — средний уровень признака из 10% наибольших значений признака в совокупности;

^xmin — средний уровень признака из 10% наименьших значений признака в совокупности.

Рассмотрим методику расчета структурных средних более подроб- но на примере решения задач.