Учебнометодический комплекс Основы банковского дела Челябинск, 2020 Должность

• Название: Учебнометодический комплекс Основы банковского дела Челябинск, 2020 Должность
• Дата: 11.04.2021
• Размер: 0.88 Mb.
• Имя файла: 2020_UMK_BD-Ivanova.doc
• Тип: Учебно-методический комплекс; #193561
• страница: 7 из 12

Тема 3.3. Банковский процент и процентные вычисления.

Способы определения и начисления процентов.
Банковский процент – одна из наиболее развитых в России форм ссудного процента, когда банк выступает в качестве одного из субъектов кредитных отношений. Уровень банковского процента в странах с рыночной экономикой определяется макроэкономическими факторами, характерными для любой формы ссудного процента, и частными факторами, лежащими в основе проведения процентной политики конкретного банка.

Макроэкономические факторы:

- соотношение спроса и предложения кредитных ресурсов;

- денежно-кредитная политика ЦБ РФ;

- Инфляционные ожидания;

- конкуренция на рынке кредитных ресурсов;

- развитие рынка ценных бумаг;

- открытость национальной экономики, международная миграция капиталов, обменный курс валют, состояние платежного баланса страны;

- фактор риска;

- система налогообложения.

Частные факторы, определяются позицией банка на рынке, характером операций и размером принимаемых рисков.

Размещая капитал в коммерческие банки, в инвестиционные проекты, в ценные бумаги и недвижимость, финансовый менеджер планирует не только со временем вернуть вложенную сумму, но и получить ожидаемый экономический эффект. В любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.

Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом наращения. Процесс, в котором заданы возвращаемая сумма и коэффициент дисконтирования называется процессом дисконтирования.
Настоящее Будущее

И сходная сумма, Возвращаемая сумма

процентная ставка наращение

П риведенная сумма Возвращаемая сумма,

дисконтирование дисконтная ставка

В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором - о движении от будущего к настоящему.

Будущая стоимость денег представляет собой сумму инвестированных в текущий момент денежных средств, в которую они перейдут через определенный период времени с учетом условий вложения. Определение будущей стоимости денег связано с процессом наращения этой стоимости.

Настоящая стоимость денег представляет собой сумму будущих денежных поступлений, приведенных с помощью определенного коэффициента (дисконта) к настоящему периоду, то есть определение настоящей стоимости денег связано с процессом дисконтирования этой стоимости.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляется процент. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают следующие методы начисления процента:

1. 
   По простым процентным ставкам. Сущность этого метода сводится к тому, что процент начисляется в течение всего срока кредита на одну и ту же величину капитала, предоставляемого в кредит.
   
2. 
   По сложным процентным ставкам. Этот метод заключается в том, что в первом периоде начисление производится на первоначальную сумму кредита, затем она суммируется с начисленными процентами, и в каждом последующем периоде процент начисляется на уже наращенную сумму.
   

Кроме того, существуют 2 способа начисления процентов.

1. 
   Декурсивный (последующий). Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Соответственно декурсивная процентная ставка (ссудный процент) представляет собой выраженную в процентном отношении сумму начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.
   
2. 
   Антисипативный (предварительный). Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженная в процентном отношении сумма дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определенная таким способом процентная ставка называется учетной ставкой или антисипативным процентом.
   

Простые проценты.
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов:

• 
  от величины капитала, предоставляемого в кредит;
  
• 
  от срока, на который предоставлен кредит;
  
• 
  от величины ссудного процента (процентной ставки).
  

Процентная ставка характеризует доходность кредитной сделки. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Процентная ставка определяется по формул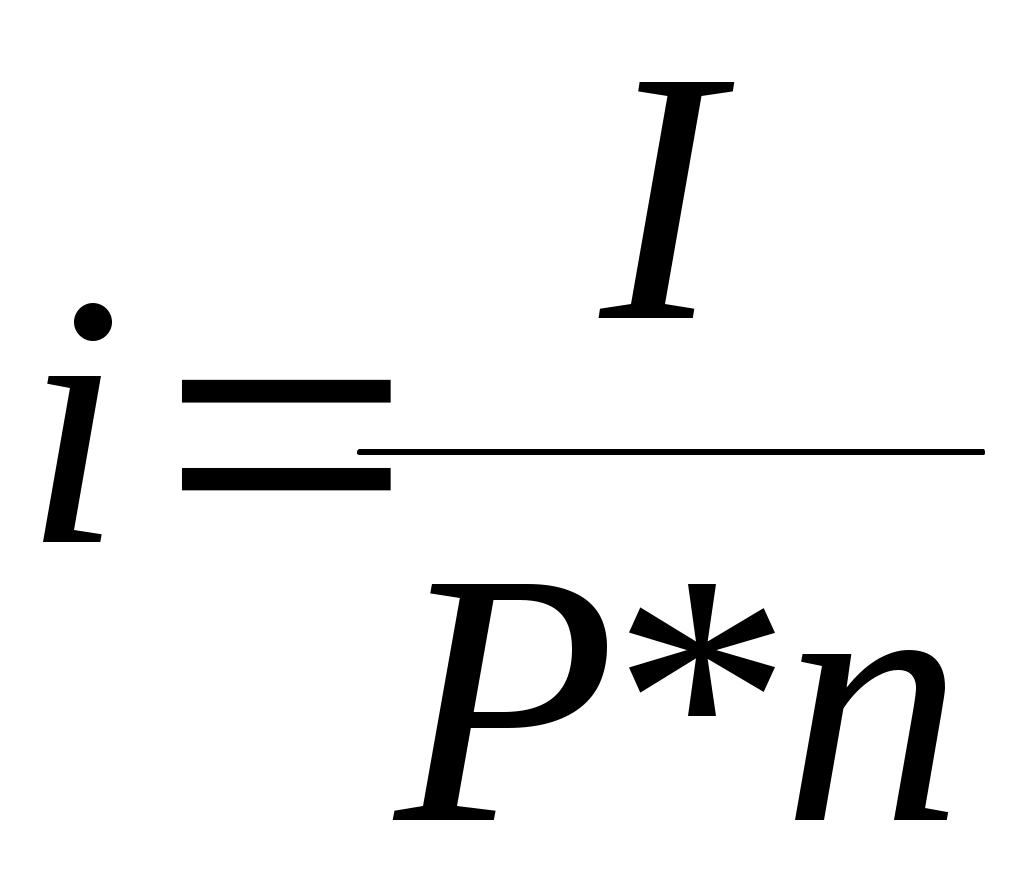е:

, где

n - срок ссуды в годах;

i - процентная ставка, выраженная десятичной дробью;

I - величина дохода владельца капитала;

P - сумма капитала, предоставляемого в кредит.



Величину "I" называют процентными деньгами или процентным доходом, а иногда просто процентами.

По условиям кредитного контракта процентные деньги могут выплачиваться кредитору или по мере начисления в каждом периоде, или совместно с основной суммой долга по истечению срока контракта. В последнем случае сумма, полученная кредитором, называется наращенной суммой (S):



При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражаются дробным числом: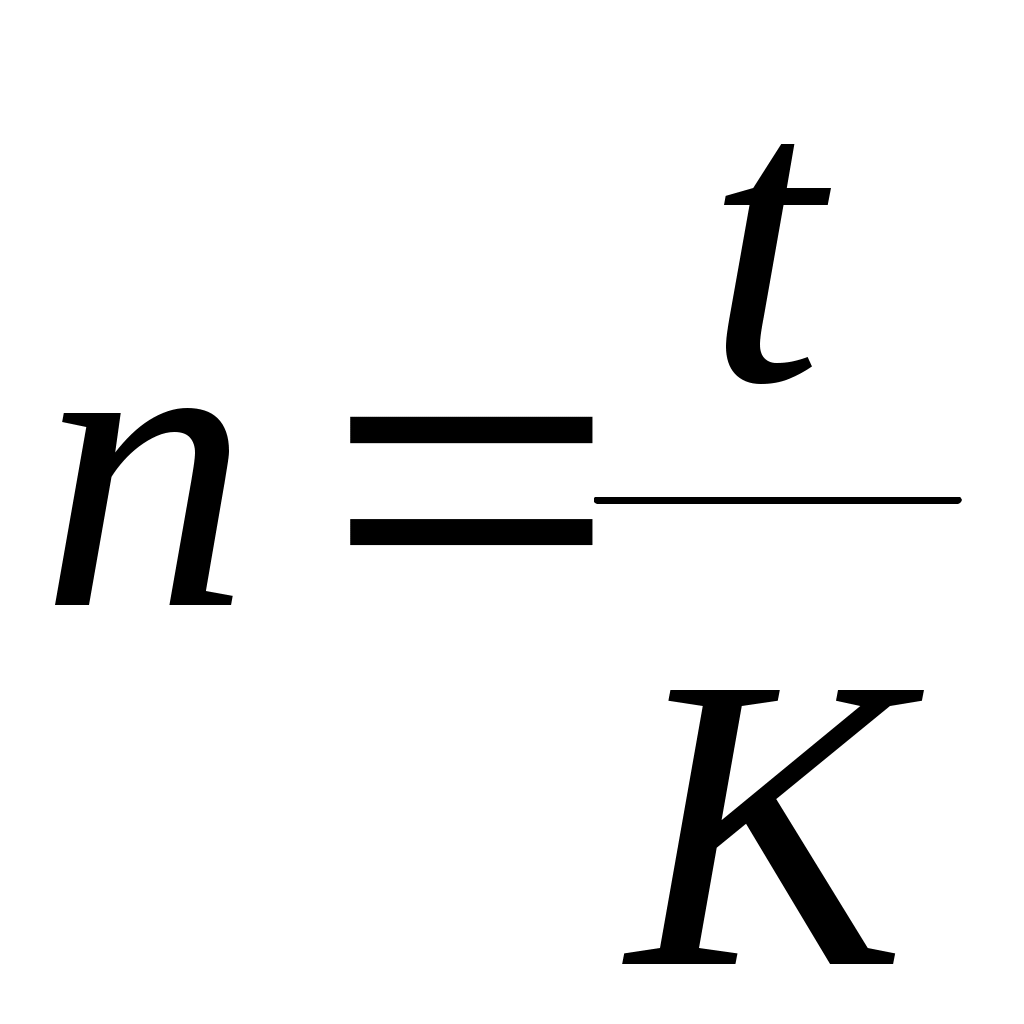

, где

t - число дней функционирования сделки (число дней, на которое предоставляется кредит);

K - число дней в году, тогда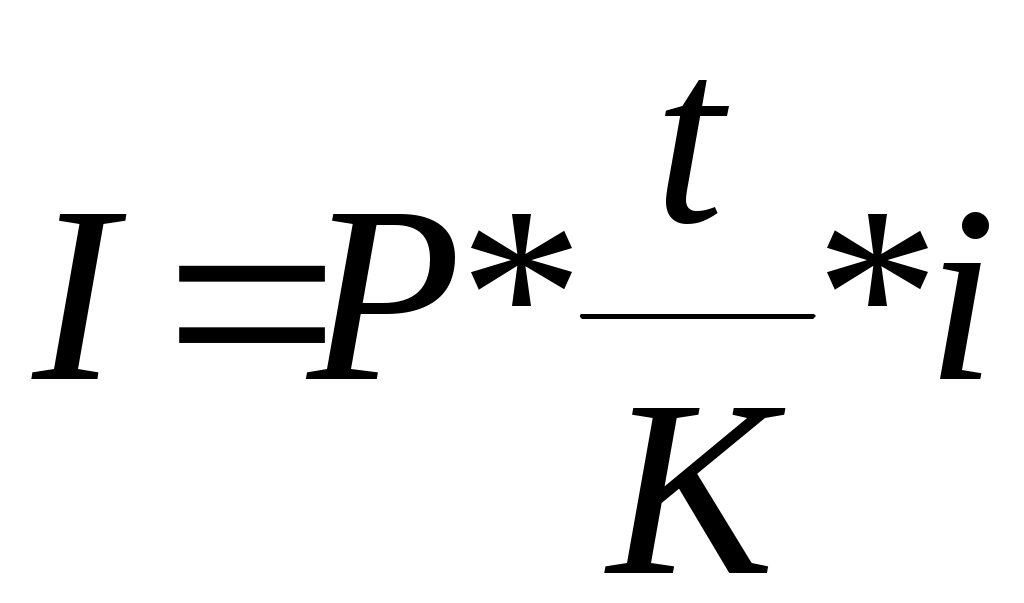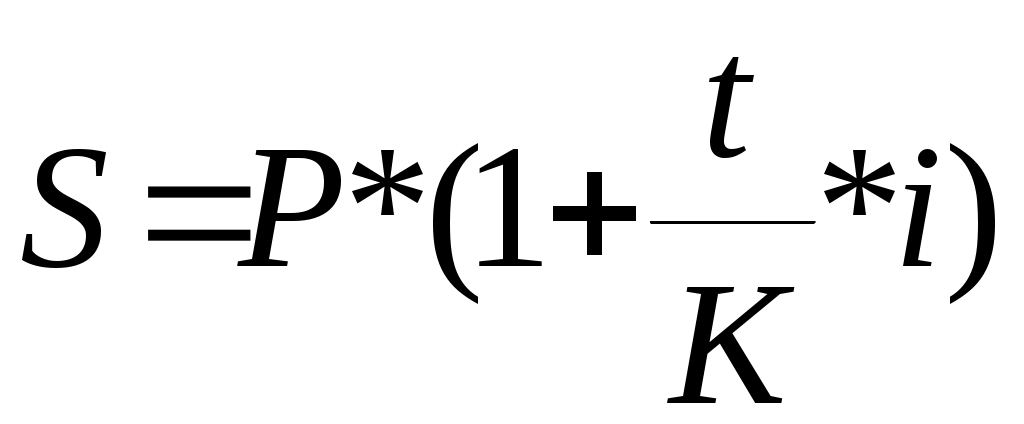

,

.

Различают 3 метода процентных расчетов, зависимых от периода начисления:

1. 
   Английская практика (точные проценты с точным числом дней ссуды). K=365 (366), а t, то есть продолжительность месяца в днях, соответствует календарному начислению.
   
2. 
   Французская практика (обыкновенные проценты с точным числом дней ссуды). К=360, а t соответствует календарному исчислению.
   
3. 
   Германская практика(обыкновенные проценты с приближенным числом дней ссуды). К=360, а t определяется количеством месяцев по 30 дней в каждом.
   

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимается за 1 день.

При установлении переменной процентной ставки (изменяющейся во времени) применяются формулы: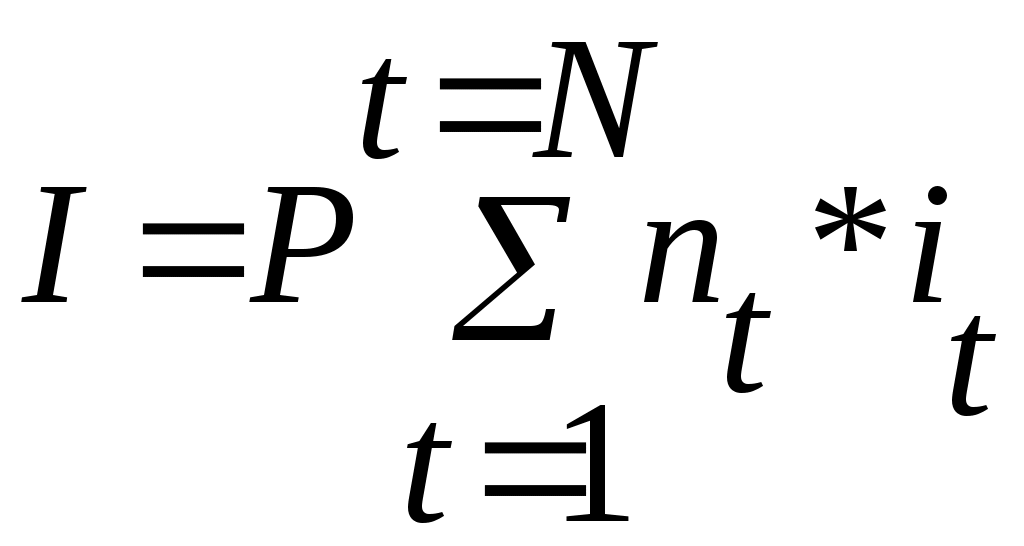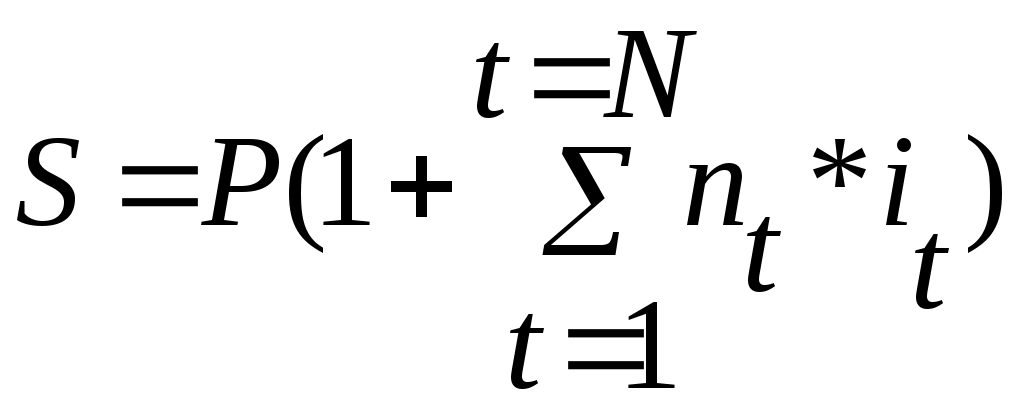

, при
, при
Сложные проценты.

В финансовой практике широко используются сложные проценты. Основное отличие сложных процентов от простых заключается в том, что база для начисления процентов меняется от одного расчетного периода к другому. Сумма начисленных в каждом периоде процентов добавляется к капиталу предыдущего периода, а начисление процентов в последующем периоде производится на эту уже наращенную величину первоначального капитала. Процесс наращения капитала в этом случае происходит с ускорением и называется капитализацией. Различают годовую капитализацию (процентный платеж начисляется и присоединяется к ранее наращенной сумме в конце года), полугодовую, квартальную, месячную, ежедневную.

Если проценты в периоде начисления начисляются по постоянной сложной ставке и все периоды начисления имеют одинаковую длительность, сумма вклада с процентами в конце первого периода будет равна:



в конце второго периода:



в конце третьего периода:



Таким образом, формула имеет следующий вид:




Дисконтирование, его сущность.

Векселедержатель (кредитор) или владелец иных долговых обязательств в случае необходимости получить деньги по векселю или другим долговым обязательствам ранее указанных в них сроков может продать его банку или другому субъекту по пониженной цене, то есть по цене ниже номинальной стоимости векселя, указанной в нем.

Такая сделка носит название учета векселя или дисконтирования. Сумма, полученная владельцем векселя в результате этой сделки, называется дисконтированной величиной. Она ниже номинальной стоимости векселя на величину процентного платежа, вычисленного со дня дисконтирования до дня, ранее предусмотренного для погашения векселя.

Дисконтом называется разность между номинальной стоимостью долгового обязательства и суммой, полученной векселедержателем в результате учета векселя. Дисконтирование векселя является по существу формой кредитования векселедержателя путем досрочной выплаты ему обозначенной в векселе суммы за минусом определенных процентов. Для субъекта сделки, принявшего к учету вексель, дисконт является доходом. Дисконт рассчитывается также на основе учетной ставки, величина которой зависит от срока, остающегося до оплаты обязательства, и существующих банковских ставок. Различают математическое и банковское дисконтирование.

При математическом дисконтировании решается задача, обратная определению наращенной суммы. Сформулируем её следующим образом: "Какую сумму следует выдать в долг на nлет, чтобы при начислении на неё процентов по ставке (i) получить наращенную сумму, равную S?"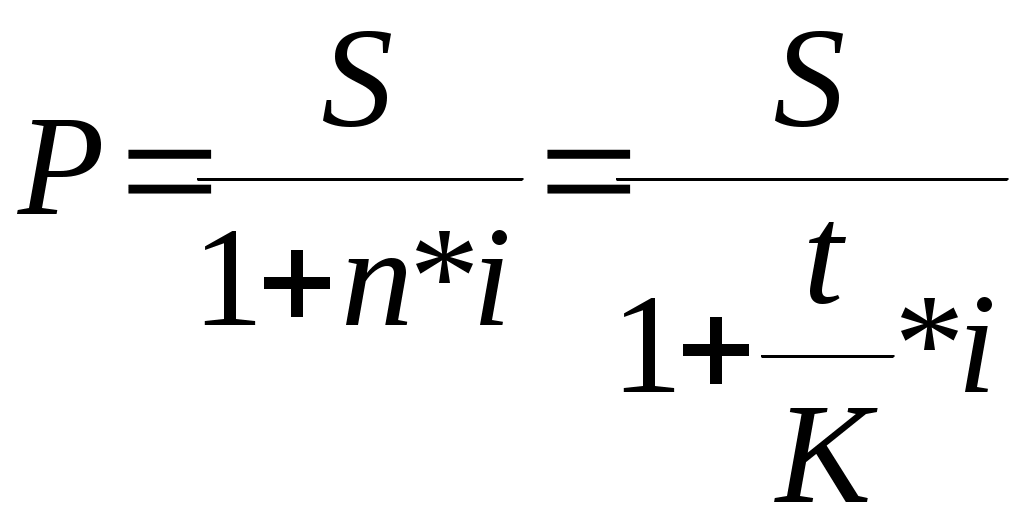





Банковское дисконтирование. Дисконт определяется по формуле:

или

Дисконтированная величина определяется по формул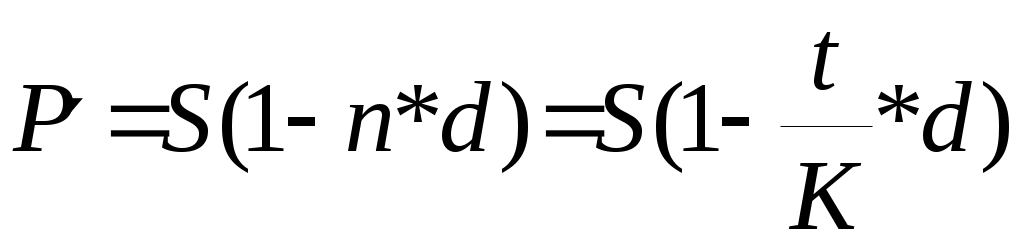е:



, где

D - дисконт или доход банка, d - учетная ставка;

S - наращенная сумма долга;

P' - дисконтированная величина (сумма, полученная владельцем векселя);

n- временной интервал от момента учета векселя до уплаты по нему в годах.
Определение сроков ссуды

При оформлении кредитного договора срок ссуды в годах и в днях определяется по формуле: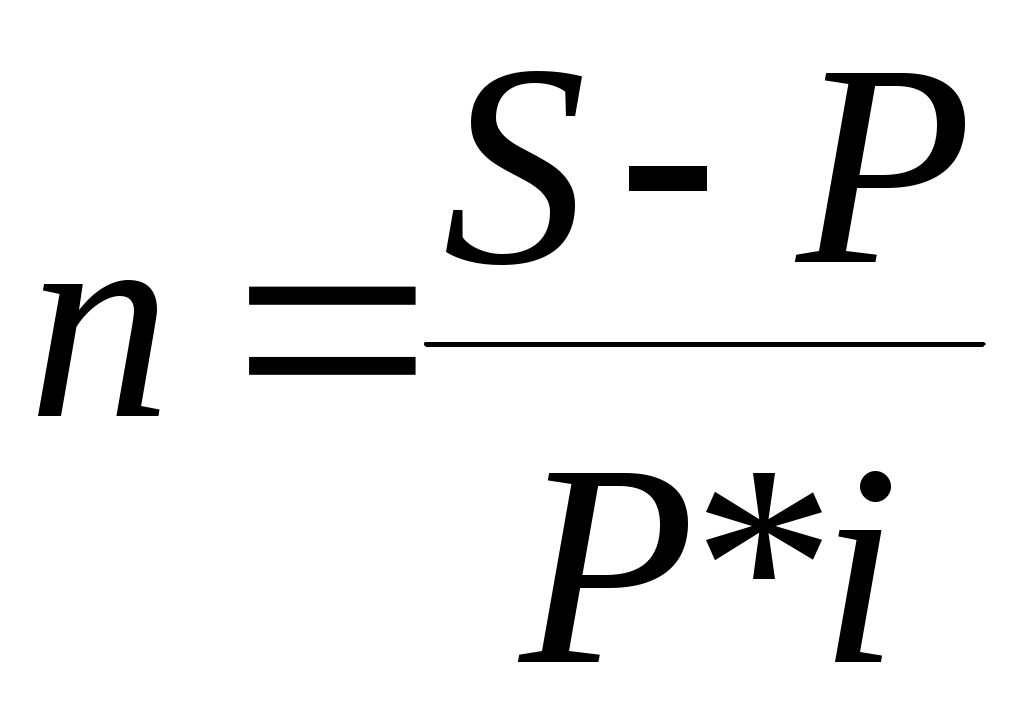



Простая процентная ставка определяется по формуле: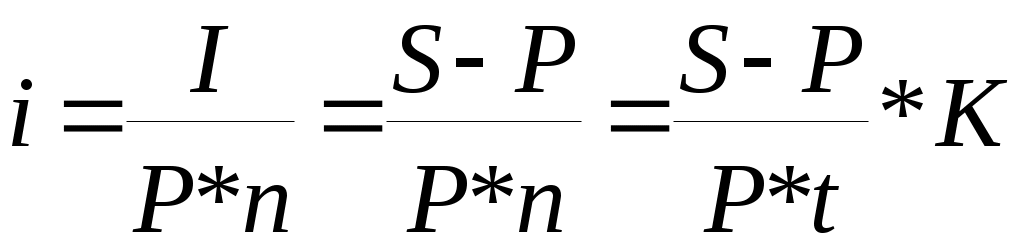



Учетная ставка определяется: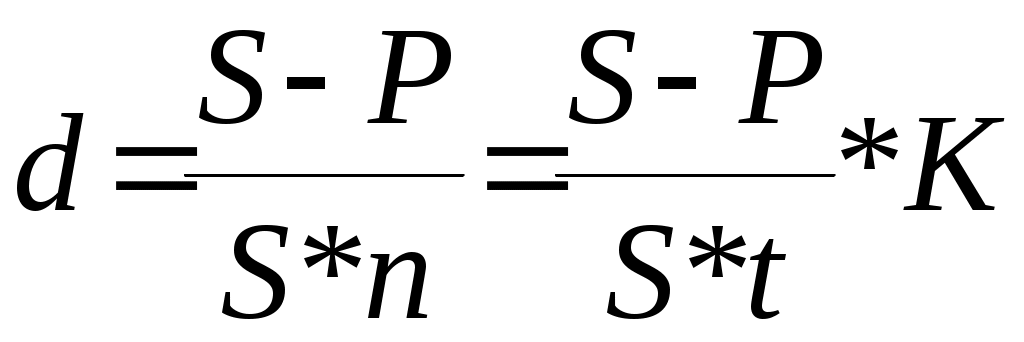

Контрольные вопросы:

1. Что представляет собой будущая стоимость денег и как она связана с процессом наращения? ___________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________
2. Что означает дисконтирование?

_____________________________________________________

__________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________

3. Раскройте декурсивный и антисипативный способы определения и начисления
процентов:

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. В чем сущность начисления простых процентов?

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5.Какие практики применяются при процентных расчетах?

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6.В чем заключается основное отличие сложных процентов от простых

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7.Какая сделка носит название учета векселя?

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
8.Дайте определение дисконта

___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9.Что называется дисконтированной величиной?

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
10. Какие особенности учитываются при определении сроков ссуды в годах и в днях?

___________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________

___________________________________________________________________________________
Практическое задание:

Задание 1. Коммерческий банк приобрел на 200млн. руб. государственных краткосрочных облигаций (ГКО) со сроком погашения через 6 месяцев. По истечении указанного срока банк рассчитывает получить по облигациям 302 млн. руб. Определить доходность ГКО?

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 2. Банк принимает во вклады до востребования по ставке 6% годовых. Определить сумму процентов на вклад 200тыс. руб., размещенный на полгода.

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задание 3. Банк выдал своему клиенту ссуду в размере 100 тыс. руб. сроком на 2 года по ставке простых процентов, равной 15% годовых. Определить проценты и наращенную сумму.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задание 4. Банк выдал кредит 18 января в размере 50 тыс. руб. срок возврата кредита 3 марта, процентная ставка установлена 15% годовых. Год не високосный. Определить наращенную сумму по трем видам практик (английской, французской, германской).

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 5. Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: первое полугодие процентная ставка – 8% годовых, каждый следующий квартал ставка возрастает на 1%. Проценты начисляются только на первоначально внесенную сумму вклада. Определить наращенную за год сумму, если вкладчик поместил в банк на этих условиях 100тыс. руб.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задание 6. Вкладчик внес в банк 500тыс. руб. под 8% годовых (проценты сложные). Определить наращенную сумму через 4 года.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 7. Депозит в размере 500 тыс. руб. положен в банк на 3 года. Определить сумму начисленных процентов при простой и сложной ставках процентов, равных 9% годовых.

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 8. Банк начисляет проценты на вклады по сложной ставке 8% годовых. Определить сумму начисленных процентов, если вклад 100тыс. руб. был востребован через 2,5 года.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 9. Вкладчик собирается положить деньги в банк с целью накопления через 1 год 50 тыс. руб. Банк начисляет проценты по ставке 10% годовых. Определить требуемую сумму вклада.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 10. Банк начисляет проценты на вклады до востребования по ставке 8% годовых с использованием германской практики. Определить, какую сумму надо положить в банк 20 мая, чтобы 5 августа того же года получить 200 тыс. руб.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 11. Вексель на сумму 500 тыс. руб. предъявлен в банк за полгода до срока его погашения. Банк для определения своего дохода использовал учетную ставку, равную 6% годовых. Определить сумму, выплаченную владельцу векселя и сумму дисконта, полученного банком.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 12. Вексель на сумму 1 млн. руб. со сроком погашения 20 декабря предъявлен в банк для оплаты 25 сентября. Банк учел вексель по учетной ставке 9% годовых. Определить сумму, выплаченную владельцу векселя и сумму дисконта при германской практике расчетов.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 13. Фирма планирует получение кредита в сумме 10 млн. руб. банк предоставляет кредит под 15% годовых. На какой срок фирма может взять кредит с тем, чтобы подлежащая возврату сумма не превысила 15 млн. руб.

___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 14. Заемщик предполагает взять кредит в размере 20000 руб. с погашением его суммой 27000 руб. Ставка банка –15% годовых. Определить, насколько дней можно взять кредит (к=365).

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 15. Вкладчик, решивший положить на депозит 80000 руб. хочет накопить через полгода не менее 100000 руб. Определить простую ставку процентов, на основании которой он может сделать выбор банка.

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 16. Рассчитать учетную ставку, которая обеспечивает получение 60000 руб., если сумма 50000 руб. выдается в ссуду на 90 дней (к=360).

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________