имитнов2008. Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности

• Название: Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности
• Дата: 28.01.2022
• Размер: 1.61 Mb.
• Имя файла: имитнов2008.doc
• Тип: Учебно-методический комплекс; #344977
• страница: 5 из 10

Повременное моделирование с переменным шагом

В процессе функционирования системы массового обслуживания можно выделить два типа состояний:

- обычные, в которых система находится почти все время;

- особые, характеризующиеся сменой состояний.

К особым состоянием относятся: поступление заявки, начало и окончание ее обслуживания, появление отказа (сбоя) в работе системы, восстановление работоспособности системы и т.п.

Если моделирующий алгоритм построен по принципу особых состояний, то он просматривает процесс функционирования только в те моменты времени, когда состояние системы меняется.

В общем случае события, вызывающие особые состояния, могут быть зависимыми.

Моменты возникновения особых состояний и их характеристики (признаки) записываются в календарь событий. В ходе моделирования может происходить корректировка календаря. Например, при поступлении заявки высшего приоритета может произойти прекращение обслуживания заявки низшего приоритета. Затем после освобождения канала возобновляется прерванный процесс обслуживания этой заявки.

Анализ календаря событий позволяет установить результаты моделирования для каждой случайной реализации. Данный метод применяется редко из-за сложности разработки алгоритма, основанного на использовании календаря событий..

Последовательная проводка заявок

При моделировании процессов обслуживания заявок в системе массового обслуживания иногда удобно строить моделирующий алгоритм по способу последовательной проводки заявок. Этот способ может быть осуществлен, если события, происходящие в системе, не зависят друг от друга.

Моделирующий алгоритм последовательной воспроизводит истории отдельных заявок в порядке их поступления в систему. Алгоритм обращается к сведениям о других заявках лишь в том случае, если это необходимо для решения вопроса о дальнейшем порядке обслуживания данной заявки. Этот способ не требует создания календаря событий.

Существуют две разновидности способа последовательной проводки:

-проводка одиночных заявок;

-проводка потоков заявок.

Рассмотрим вначале первый вариант. Пусть, например, в одноканальную систему массового обслуживания в одной случайной реализации процесса поступили четыре однородные заявки(с одинаковым приоритетом), как показано на рисунке 11.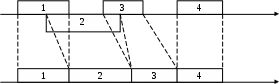








0


Рисунок 11- Последовательная проводка заявок

В случайный момент времени в систему поступила 1-я заявка. Поскольку канал свободен, ее обслуживание начинается в момент времени . Если распределение времени обслуживания известно, то с помощью жребия можно определить случайную величину времени обслуживания . Тогда момент окончания обслуживания 1-й заявки будет равен : . При этом к счетчику числа обслуженных заявок прибавляется единица.

Далее определяется время поступления 2-й заявки. Если распределение случайной величины времени между соседними заявками известно, то с помощью жребия можно определить интервал между 1-й и 2-й заявками и найти момент времени поступления 2-й заявки . Поскольку канал занят, для 2-й заявки начинается период ожидания продолжительностью . Обслуживание этой заявки начинается в момент . Далее с помощью жребия определяется случайная величина времени обслуживания 2-й заявки . Тогда момент окончания обслуживания 2-й заявки будет равен: . К счетчику числа обслуженных заявок прибавляется единица.

Аналогичным образом обслуживаются 3-я и 4-я заявки.

Вторым вариантом способа последовательной проводки заявок является способ, при котором вначале формируется поток заявок, а затем начинается процесс обслуживания заявок. При этом предполагается, что все заявки однородные. В этом случае для хранения данных о заявках в памяти ЭВМ необходимо создавать массивы чисел. Поскольку размерность такого массива заранее неизвестна, приходится выбирать ее с определенным запасом, что приводит к напрасному расходу памяти.

Поэтапная последовательная проводка заявок.

Рассмотрим систему, предназначенную для обслуживания заявок двух различных приоритетов. Сделаем следующие допущения:

- все заявки независимы;

- при обслуживании используется абсолютный приоритет, т.е. поступающая заявка высшего приоритета немедленно вытесняет обслуживаемую заявку низшего приоритета;

- после освобождения канала может производиться «дообслуживание» той заявки второго приоритета, которая была вытеснена заявкой первого приоритета.

При этих допущениях для построения моделирующего алгоритма может быть применен усовершенствованный способ последовательной проводки, который можно назвать способом поэтапной последовательной проводки.

Первый этап моделирования.

Распределение случайных величин интервалов между соседними заявками первого приоритета будем считать известны. Если задать интенсивность потока, то с помощью датчика случайных чисел можно определить случайные моменты поступления заявок и т.д. Распределение случайного времени обслуживания будем также считать известным. Если задать среднее время обслуживания, то с помощью датчика случайных чисел можно заранее определить случайные интервалы обслуживания (рисунок 12)
Поток заявок первого приоритета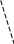






0

Обслуживание заявок первого приоритета



0



Поток заявок второго приоритета






Обслуживание заявок второго приоритета





0

Рисунок 12 - Поэтапная последовательная проводка заявок
Установим модельное время на нуль. Будем рассматривать изолированный поток заявок первого приоритета так, как будто заявок второго приоритета не существует.

Применив способ последовательной проводки, можно установить моменты начала и окончания обслуживания заявок первого приоритета. Иначе говоря, в результате выполнения первого этапа моделирования можно определить значения элементов массива и элементов массива .

Можно также подсчитать число обслуженных заявок до конца периода обслуживания .

В данном случае заявки 1.1 и 1.3 обслуживаются сразу после их поступления, а заявка 1.2 обслуживается после некоторого ожидания, связанного с занятостью канала.

Второй этап моделирования

Вновь установим модельное время на нуль. Начинается этап моделирования процесса обслуживания заявок второго приоритета в условиях, что на временной оси располагаются уже обслуженные заявки первого приоритета. Следовательно, заявки второго приоритета могут занимать только свободные промежутки времени.

Распределение времени между соседними заявками будем считать известным. Тогда с помощью жребия можно определить возможные значения случайных величин времени поступления заявок. Распределение времени обслуживания также будем считать известным. Тогда с помощью жребия можно определить планируемые интервалы времени обслуживания.

Заявка 2.1 поступает в момент, когда канал занят обслуживанием 1.2. Затем канал освобождения и начинается обслуживание заявки 2.1. Однако, поступившая заявка первого приоритета 1.3 вытесняет заявку 2.1. Только после освобождения канала происходит процесс «дообслуживания» заявки 2.1. Заявка 2.2 также некоторого время ожидает начала обслуживания, а затем обслуживается до конца. Для заявки 2.3 не хватает времени, так как наступает конец периода обслуживания.

Рассмотрим теперь, как формализуется процесс обслуживания заявок второго приоритета в присутствии заявок первого приоритета. При взаимодействия заявок двух различных приоритетов могут возникнуть три возможные ситуации.

Ситуация 1. Ни одна из имеющихся -заявок первого приоритета не препятствует обслуживанию заявки второго приоритета. Два возможных варианта этой ситуации иллюстрируются схемой, показанной на рисунке 13.


Т





Т


Рисунок 13 - Схемы вариантов 1-й ситуации:

а-первый вариант; б-второй вариант
Здесь -фактическое время начала обслуживания i-й заявки первого приоритета;

-фактическое время окончания обслуживания i-й заявки первого приоритета;

-первоначально намеченное время начала обслуживания j-й заявки второго приоритета (без учета возможности поступления заявки первого приоритета);

-первоначально намеченное время окончания процесса обслуживания j-й заявки второго приоритета(без учета возможности поступления заявки первого приоритета).

Логическое условие, при котором создается 1-й или 2-й вариант 1-й ситуации, записывается так:

(1)

Если для j-й заявки второго приоритета условие (1) выполняется по отношению ко всем заявкам первого приоритета ( ), то j-я заявка может быть обслужена. Ей может помешать только другая заявка 2-го приоритета, принятая ранее к обслуживанию.

Ситуация 2. Система приняла к обслуживанию заявку второго приоритета, и она начала обслуживаться Однако до истечения расчетного времени окончания обслуживания поступила заявка первого приоритета, которая вытесняет данную заявку второго приоритета. Два возможных варианта этой ситуации иллюстрируется схемой, показанной на рисунке 14.

Логическое условие, при котором создается любой из вариантов 2-й ситуации, записывается так:

(2)










Т




Рисунок 14 Схемы вариантов 2-й ситуации: а -первый вариант, б -второй вариант
Если условие (2) выполняется хотя бы для какой-либо пары значений переменных и при изменении i от 1 до , то продолжение процесса обслуживания заявки второго приоритета откладывается до момента освобождения канала.

После этого рассматривается возможность «дообслуживания» заявки. С этой целью производится корректировка времени начала и окончания обслуживания заявки по формулам:





где -фиксированное время начала обслуживания заявки первого приоритета, для которой выполняется условие (2);

-фиксированное время окончания обслуживания заявки первого приоритета, для которой выполняется условие (2).

После этого вновь рассматривается возникшая ситуация.

Ситуация 3.Заявка второго приоритета поступила в период обслуживания заявки первого приоритета. Следовательно, заявка второго приоритета не может быть принята к обслуживанию. Два возможных варианта этой ситуации иллюстрируются схемой, показанной на рис. 5














Рисунок 15 - Схемы вариантов 3-й ситуации: а-первый; б-второй вариант

Логическое условие, при котором создается любой из вариантов 3-й ситуации, записывается так:

(3)

Если условие (3) выполняется для какой-либо пары значений переменных и при изменении i от 1 до , то производится «сдвиг» времени начала и окончания обслуживания заявки по формулам:

;



После этого вновь рассматривается возникшая ситуация для «сдвинутой» заявки.

«Дообслуживаемая», или «сдвинутая», заявка, в свою очередь, может оказаться в одной из трех перечисленных выше возможных ситуаций.

В конечном счете процесс обслуживания может иметь два исхода:

1. 
   заявка будет обслужена до конца;
   
2. 
   истечет время функционирования системы и заявка останется необслуженной (так же, как и все последующие заявки второго приоритета).
   

Основная литература: 1[ 30-40]

Контрольные вопросы:

1. 
   Перечислить этапы разработки математических моделей.
   
2. 
   Для чего проводят машинные эксперименты.
   
3. 
   Перечислите разновидности СМО.
   
4. 
   Что такое относительный приоритет?
   
5. 
   Что такое абсолютный и смешанный приоритет?
   
6. 
   Перечислите способы построения моделирующих алгоритмов.
   
7. 
   Что такое обычные и особые состояния?
   

Тема лекции № 4. Общая структура моделирующего алгоритма

Общая структура моделирующего алгоритма должна обеспечить достижение основной задачи имитационного моделирования – нахождения оптимального варианта или оптимальных значений параметров исследуемой системы. Для достижения этой цели необходимо, во –первых, уметь моделировать процесс функционирования системы на любом заданном интервале времени, во-вторых, обеспечить требуемую точность и достоверность полученных значений характеристик и показателей системы при условии учета различных случайных факторов и, в-третьих, иметь возможность поиска оптимальных вариантов системы [x].

Указанные требования предопределяет общую структуру моделирующего алгоритма, включающую три уровня или три цикла моделирования.(рисунок 16) Внутренний цикл (блоки 5-8) позволяет моделировать поведение системы по заданной модели на интервале [0,T].

В следующем цикле, включающем блоки с 3 по 10 организуются N- кратное повторение прогона, позволяющее после соответствующей статистической обработки результатов (блок 11), судить об усредненных характеристиках моделируемого варианта системы. Окончание варианта может определяться не только заданным числом прогонов, как показано на рис 1. (блок 10), но и заданной точностью результатов.

Внешний цикл охватывает оба предшествующих цикла и включает дополнительно блоки 1,2,11,12, управляющие последовательностью моделирования вариантов системы. Здесь организуется, в частности, поиск оптимальных параметров системы: блок 11 осуществляет проверку, удовлетворительны ли показатели системы, а блок 1 производит изменения параметров так, чтобы улучшить эти показатели.

Следует отметить, что во многих случаях, когда нет надобности рассматривать различные варианты системы, можно ограничиться двухуровневой структурой моделирующих алгоритмов.

Планирование эксперимента.

Главной особенностью этапа экспериментирования при имитационном моделировании является то, что из-за учета действия различных случайных факторов результаты моделирования также носят случайный характер. Поэтому для обеспечения заданной точности полученных оценок необходимо усреднять результаты большого количества реализаций. Для определения количества реализаций необходимо установить зависимость между точностью оценки, количеством реализаций и доверительной вероятностью. Найдем количественную связь между указанными величинами для различных оценок случайных величин и процессов.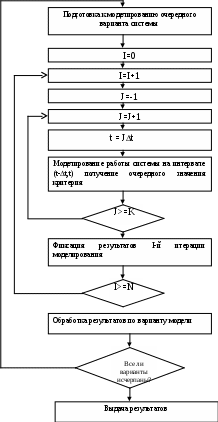





1) Определение количества реализаций для оценки вероятности

Вероятность р оценивается отношением, где m – число случаев наступления события А при N реализациях. Это отношение можно представить в иной форме

(4)

где - дискретная случайная величина с законом распределения



Определим математическое ожидание и дисперсию оценки р

(5)

. (6)

Теперь установим зависимость между точностью оценки Е, Е количеством реализаций N и доверительной вероятностью :



В силу центральной предельной теоремы теории вероятностей оценка (4) при достаточно больших N имеет распределение, близкое к нормальному. Поэтому из таблицы нормального распределения для каждого значения доверительной вероятности  можно выбрать величину такую , что точность оценки будет равна

(7)

Подставляя (4-5) в (7), получим искомое выражение для количества реализации при оценке вероятности

(8)

Из (8) следует, что для определения N необходимо знать значения оцениваемой вероятности р, которое обычно неизвестно. Поэтому практически всегда производят предварительную «пристрелку», назначая какое-либо число реализаций N₀ и определяя р₀К/N₀. Затем найденное р поставляют в (8).

2) Выбор N при оценке математического ожидания и дисперсии.

Для оценки математического ожидания случайной величины используется среднее арифметическое .

Пусть необходимо построить такую оценку истинного математического ожидания m , что .

По центральной предельной теореме при большом N среднее арифметическое имеет распределение, близкое к нормальному с математическим ожиданием m и дисперсией , где дисперсия оцениваемой случайной величины. Поэтому, подставляя в формулу, аналогичную (7), дисперсию будем иметь



Следовательно



Так как заранее неизвестна, то вместо нее используется оценка , полученная по формуле

,

В результате предварительной «пристрелки» с числом реализаций N₀ .

Определим число реализаций N, необходимое для получения оценки дисперсии. При этом предполагается, что

,

где 0   1 – число, характеризующее степень близости оценки к истинной дисперсии .

Так как распределена асимптотически нормально с параметрами

;

То пренебрегая и учитывая, что в случае нормального распределения оцениваемой случайной величины

Получим

Следовательно .

Для определения  здесь также используется «пристрелка».

Регенеративный метод анализа результатов моделирования

Этап обработки результатов имитационного моделирования также имеет свою особенность. Она связана с тем, что многие объекты имитационного моделирования обладают свойством время от времени регенерироваться, т.е. стохастические процессы, протекающие в таких системах, постоянно возвращаются в некоторую точку (точку регенерации), начиная с которой дальнейшее развитие процесса не зависит от его поведения в прошлом и определяется одним и тем же вероятностным законом. Если результаты моделирования таких систем группировать в соответствии с последовательными возвращениями в точку регенерации, то эти группы статистически независимы и одинаково распределены, что сильно облегчает их статистический анализ.

Последовательность случайных векторов размерности К является регенерирующим процессом, если существует возрастающая последовательность



случайных дискретных моментов времени, называемых моментами регенерации, такая, что протекание процесса, начиная с каждого из этих моментов, определяется теми же вероятностными законами, что и в момент . Часть процесса в интервале будем называть j-м циклом. Введем также понятие периода регенерации

.

Эти периоды являются независимыми и одинаково распределенными величинами.

Пусть далее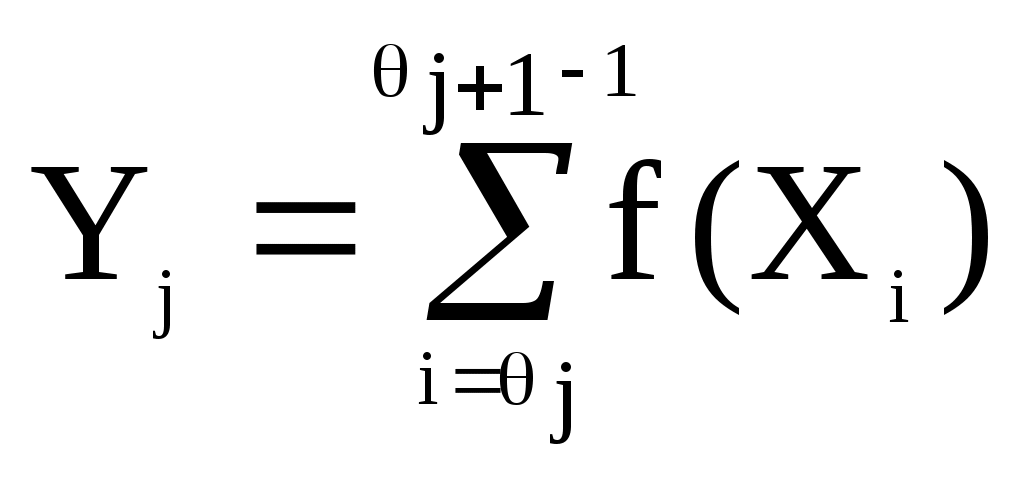

,

где - некоторая функция от К аргументов, принимающих действительные значения. Соответствующим выбором функции f можно оценить достаточно широкий класс стационарных характеристик, представляющих практический интерес.

Далее примем, что моделирования состоит в оценке значения М[f(X)].

Так как является суммой значений на j-м цикле (j-й группе), то последовательность ( ) состоит из независимых и одинаково распределенных случайных векторов. При достаточно слабом предположении, что ,

можно получить выражение

. (9)

Действительно

(10)

При N.

И если n-й цикл завершается в момент N, то отношение в (9) можно записать иначе:

(11)

Но отношение (11) с вероятностью 1 сходится к при n. И, следовательно, получим соотношение (9). Таким образом, можно констатировать, что задача оценки такая же, как и оценка отношения, которое на основе классической статистики, можно оценить по независимым и одинаково распределенным парам

.