имитнов2008. Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности

• Название: Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности
• Дата: 28.01.2022
• Размер: 1.61 Mb.
• Имя файла: имитнов2008.doc
• Тип: Учебно-методический комплекс; #344977
• страница: 9 из 10

Шаг 2. Проверить неравенство Т4. При выполнении неравенства перейти к шагу 3, а при невыполнении – к шагу 4.

Шаг 3. Вычислить Т = Т-4.

Шаг 4. Принять Z₁ = Т и вычислить очередное значение равномерной последовательности по формуле Z_j+1=R=T/4.

Перейти к шагу 1.

Задание 2.Метод возмущения Д.И. Голенко

Назначение – увеличение длины отрезка апериодичности базовой последовательности случайных чисел.

Принцип работы. Для получения последовательности с большим значением отрезка апериодичности Д.И. Голенко предложил использовать 2 алгоритма. Основанных на рекуррентных формулах с различными функциями: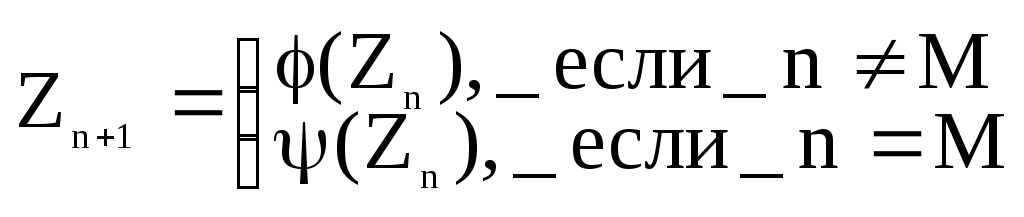



где M – период возмущения (рисунок 29)

Z_n+1=Ф(Z_n) Z_n+1=Ф(Z_n) Z_n+1=Ф(Z_n)



Z₀ Z₁ Z₂ Z_M-1 Z_MZ_M+1 Z_2M-1 Z_2MZ_2M+1

Z_n+1=Ψ(Z_n)

Рисунок 29

Методические рекомендации: Практическая реализация метода возмущения заключается в следующем. Выбрав период возмущения, производим вычисления по 2-му алгоритму только в точках, кратных периоду возмущения. Все остальные значения вычисляются по рекуррентному соотношению 1-го алгоритма.

Составить блок-схему алгоритма для метода возмущения Д.И.Голенко, в качестве I –го алгоритма использовать алгоритм «середины квадратов», а в качестве II-го – алгоритмом Дэвиса.

Основная литература: 5, 9

Контрольные вопросы:

1Просчитать численный пример для следующих начальных значений: n=10, P=5, k=2, a=302, c=4965, m=42782, x=120 методом возмущения Д.И. Голенко.

2. Что называется базовой последовательности?
Практическое занятие № 3. Моделирование случайных событий

Задание 1. Моделирование простых событий

Назначение – моделирование случайного события с заданным вероятностью.

Принцип работы. Пусть событие А наступает с вероятностью .

Теорема 2.1. Пусть р вероятность наступления события А, а Z –независимая реализация случайной величины . Тогда для наступления события А необходимо выполнение условия

Z  p.

Доказательство:

Алгоритм, реализующий условие этой теоремы, включает 7 шагов.

Шаг 1. Положить j=1.

Шаг 2. Получить реализацию Z случайной величины .

Шаг 3. Проверить условие Z  p. При нарушении этого условия перейти на шаг 5.

Шаг 4. Фиксировать число S наступления события А.

Шаг 5. Положить j=j+1.

Шаг 6. Проверить условие j>n , где n – число независимых испытаний.

Задание 2. Моделирование группы событий

Назначение – моделирование полной группы несовместных событий с заданными вероятностями.

Принцип работы. Пусть А₁, А₂, …, А_n – полная группа несовместных событий с заданными вероятностями Р(А_i)=P_i причем, .

Пусть случайная величина  - номер наступившего события. Распределение  задается в виде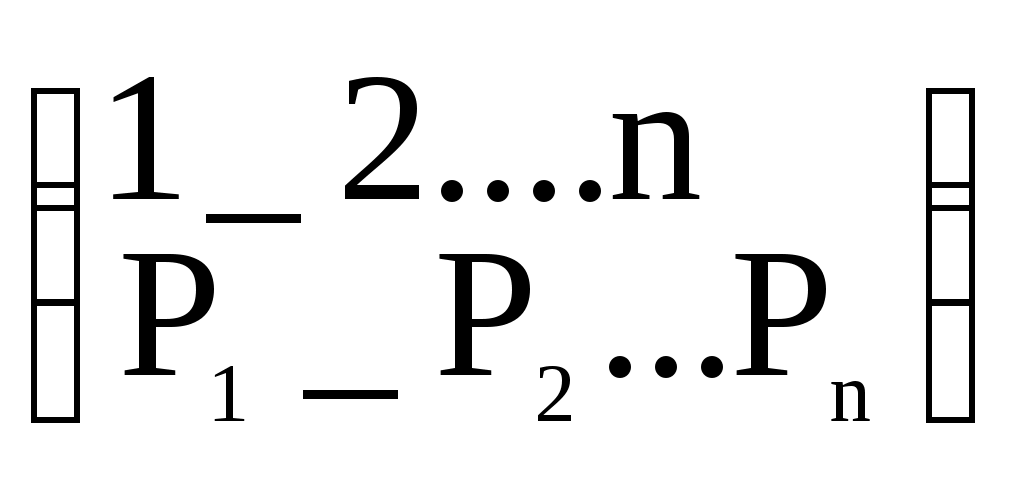

(3.1.)

Разделим интервал [0.1] на подынтервалы ∆_i такие, что длина ∆_i равна P_i (рисунок 2).

∆₁ ∆₂∆₃∆_np

0P₁ P₁ +P₂ P₁ +P₂+P₃ 1 –P_n1

Рисунок 2

Теперь сформулируем теорему 3.2. Случайная величина  , определенная формулой

 = i, когда z ∆_i, (3.2)

имеет распределение вероятностей (3.1).

Методические рекомендации: Практическое использование утверждения теоремы осуществляется следующим образом. Моделируется очередная реализация Z случайной величины  и сравнивается с Р_{1 .} Если Z Р₁, то Z сравнивается с Р₁+ Р₂. Если Z> Р₁+ Р₂ – Z сравнивается с Р₁+ Р₂ + Р₁+ Р₃ и т. д.

Эту схему моделирования полной группы событий можно формализовать в виде следующего алгоритма:

Шаг 1. Моделируется очередная реализация Z случайной величины , равномерно распределенной на интервале [0.1].

Шаг 2. Рассматривается возможность выпадения события А₁, т.е. Принимается, что

i =1.

Шаг 3. Проверяется неравенство

(3.3)

При невыполнении неравенства (3,3) переход к шагу 5.

Шаг 4. Рассматривается следующее событие с номером i =i +1. Возврат к шагу 3.

Шаг 5. Фиксируется выпадение события А_i

Изучите моделирование случайных событий и составьте блок-схему алгоритма моделирования простых событий и алгоритма моделирования полной группы событий.

Основная литература: 5,9

Контрольные вопросы:

1. Просчитать численный пример для следующих значений:

N=200, C=5942, P=0.3 , M=32777, Z₀=118, A= 400, P=0.3.Найти количество наступления событий k.

2.Просчитать численный пример для следующих значений:

N=200, L=4, A=400, M=32777, Z₀=118, P₁= 0.3, P₂=0.2, P₃=0.3, P₄=0.2.

Найти количество наступления группы событий.

Практическое занятие № 4. Моделирование дискретных случайных величин

Задание 1. Моделирование сложных событий

Определение. Событие называется сложным, если результат его исхода зависит от двух и более простых событий. Сложные события делятся на независимые и зависимые. Сложное событие является независимым, если составляющие его простые события также независимы.

Методические рекомендации: Принцип работы.

Алгоритм, реализующий условия этой теоремы применительно к сложному событию, состоящему из двух простых событий А и В, имеет следующий вид.

Шаг 1. Положить j=1.

Шаг2 Получить две независимые реализации Z_j, Z_j+1 случайной величины 

Шаг 3. Проверить выполнение условий

Z_jP_Aи Z_о+1P_В

Шаг 4. В зависимости от результатов сравнений на шаге 3 прибавить единицу к одному из счетчиков:

, , , .

Шаг 5. Положить j=j+2

Шаг 6. Проверить условие j< 2n, где n – заданное число испытаний. При выполнении этого условия переход на шаг 2.

Шаг 7. Вывод содержимого счетчиков.

Задание 2. Моделирование дискретных случайных величин

Назначение – моделирование дискретных случайных величин, законы распределения которых заданы как в виде таблиц, так и с помощью известных формул (геометрическое распределение, распределение Пуассона и др.).

Принцип работы. Для моделирования дискретных случайных величин , заданных таблицей распределения вида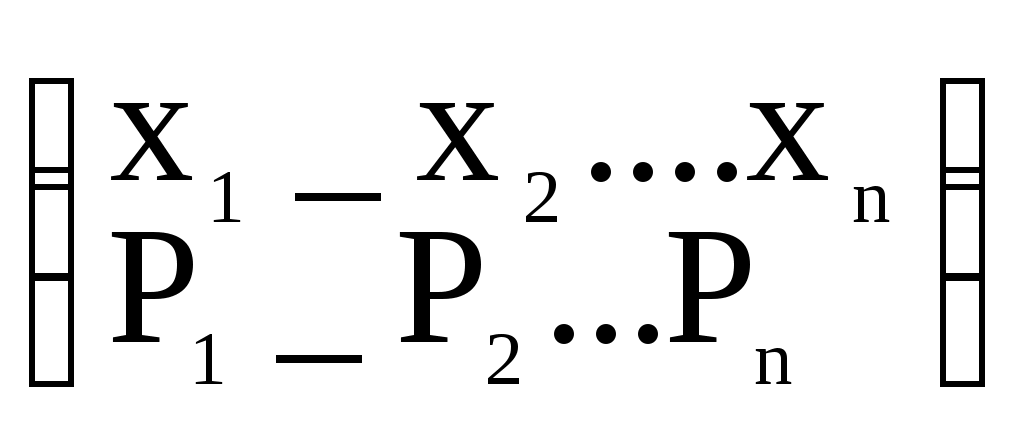

(4.1)

 = x_{i ,} когда Z ∆_i(4.2)

Геометрическое распределение

Определение .Если некоторое событие происходит с вероятностью Р, число независимых испытаний, необходимых, чтобы это событие произошло, подчиняется геометрическому распределению. Для этого распределения

Выработка значений дискретной случайной величины с геометрическим распределением, когда Р мало, осуществляется по формуле

(4.3)

где [ ] – целая часть.

Распределение Пуассона.

Определение. Случайная величина η, принимающая целые неотрицательные значения, распределена по закону Пуассона, если

, k = 0, 1, 2,…, (4.4)

где λ – среднее число событий, имеющих место в единицу времени.

Методические рекомендации: Принцип моделирования случайной величины с пуассоновским распределением основывается на предельной теореме Пуассона: если P_n – вероятность наступления события А при одном испытании, то вероятность наступления к событий при n независимых испытаниях при n→∞ и P_k→0 асимптотически равна .

Алгоритм моделирования.

Шаг 1. Моделируется реализация Z случайной величины ξ, равномерной на интервале [0.1].

Шаг 2. Проверяется условие Zn. При невыполнении этого условия возвращаются к шагу 1, т.е. переходят к следующему испытанию.

Шаг 3. К содержимому специального счетчика прибавляется единица. Переход к шагу 1.

После проведения n сравнений содержимое счетчика считывается и используется в качестве очередной реализации случайной величины η с распределением Пуассона.

Изучить моделирование дискретных случайных величин и составить блок-схему алгоритма моделирования сложных событий, алгоритма моделирования геометрического значения для малого значения P и алгоритма моделирования распределения Пуассона.

Основная литература:5.9

Контрольные вопросы:

1.Показать, что сумма двух независимых пуассоновских случайных величин с математическими ожиданиями ₁ и ₂ является также пуассоновской величиной с ожиданием, равным ₁+₂. Как распределена сумма двух независимых, нормально распределенных случайных величин ?

2. Что такое геометрическое распределение?

3.Что такое распределение Пуассона?

4.Сформулировать теорему, определяющих условия моделирования дискретных случайных величин?

5. Какое событие называется сложным?
Практическое занятие № 5. Моделирование непрерывных случайных величин

Задание 1. Метод обратной функции

Назначение – моделирование непрерывной случайной величины с произвольно заданным законом распределения.

Область применения – плотность вероятности моделируемой случайной величины должна выражаться через элементарные функции, позволяющие осуществить интегрирование.

Принцип работы. Пусть имеется непрерывная случайная величина η в интервале (а,b), f(x) > 0 – плотность вероятности для нее, F(x) – функция распределения η, которая при а<x<b имеет вид:

.

Теорема. Случайная величина η, удовлетворяющая уравнению:

F(n) = ξ (5.1)

Имеет плотность распределения f(x). Следовательно, взаимнооднозначная функция , полученная решением относительно η уравнения (5.1), преобразует величину ξ в величину η с требуемой плотностью распределения вероятностей f(x).

Методические рекомендации: Для практического использования метода необходимо разрешить относительно x_iуравнение: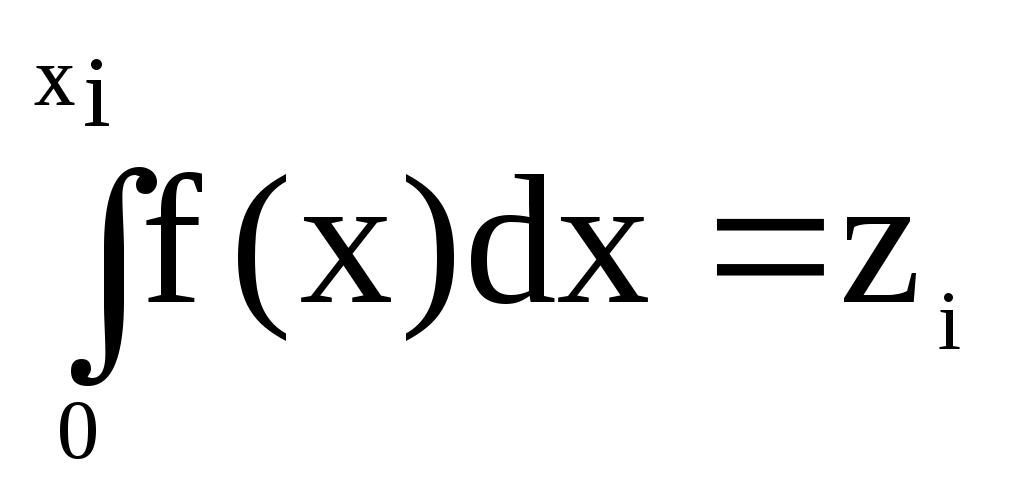

, (5.2)

где Z_i – реализация базовой случайной величины ξ, а x_i – искомая реализация моделируемой случайной величины η.

Пример. Пусть требуется получить реализацию случайной величины η с законом распределения f(x) = 2x. На основе (5.2) имеем: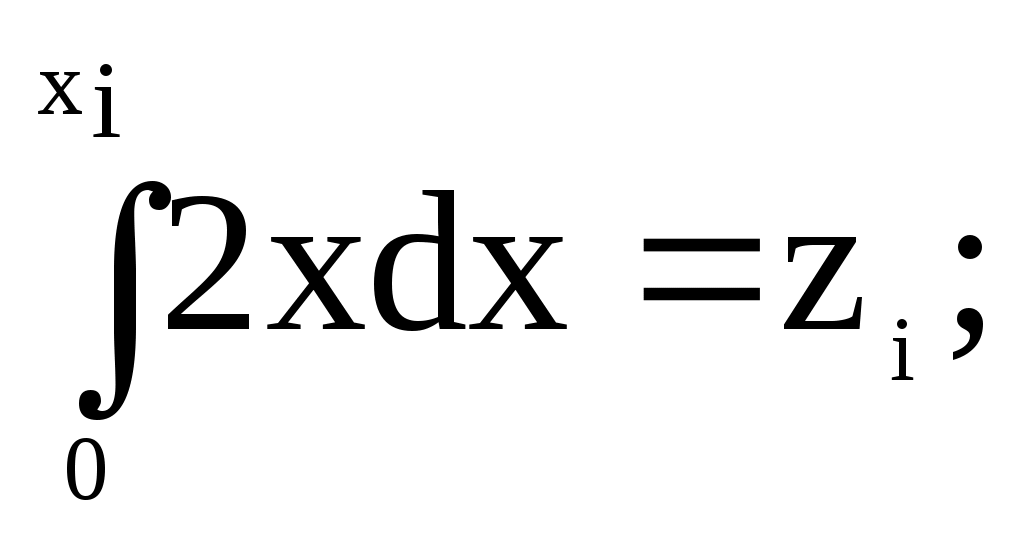



=Z_i



Задание 2. Метод исключения Неймана

Назначение метода – моделирование непрерывной случайной величины с заданным законом распределения путем отбора из базовой совокупности случайных чисел таких реализаций, которые подчиняются заданному закону распределения.

Область применения. Моделируемая случайная величина должна быть определена на конечном интервале [а,b] и иметь ограниченную сверху функции плотности, причем, эта функция может быть задана не только аналитически, но и графически.

Методические рекомендации: Принцип работы метода при условии, что случайная величина η определена на конечном интервале [a,b] и ее функция плотности ограничена f(x)≤M., основывается на теореме: пусть Z₁ и Z₂ - независимые реализации базовой случайной величины ξ и x = a + Z₁(b-a), y= MZ₂. Тогда случайная величина η, определенная условием η = x , еслиy < f(x) имеет плотность вероятностей, равную f(x).

Методические рекомендации: Практическая реализация. Алгоритм реализации метода исключения Неймана имеет вид:

Шаг 1. Генерируются 2 независимые реализации Z_i, Z_i+1 базовой случайной величины ξ с равномерным законом распределения на [0.1].

Шаг 2. Вычисляются значения x и y по формулам:

x = a + z_i (b-a);

y = M*Z_i+1 (5.3)

Шаг 3. Проверяем справедливость неравенства: y<F(x)

При невыполнении этого условия необходимо перейти к шагу 1.

Шаг 4. За реализацию случайной величины η принимается число x = a + z_i (b-a).

Использовать метод обратной функции для преобразования случайных чисел, полученных в задании 1) случайную выборку из непрерывного распределения со следующей функцией плотности вероятности:



Основная литература: 5,9

Контрольные вопросы:

1. Использовать метод обратной функции для преобразования случайных чисел из задания 1) в выборку из дискретного распределения со следующей функцией вероятности: Р(0)=1/5; Р(1)=1/5; Р(2)=2/5; Р(3)=1/5.Решить методом обратной функции.

2. Назначение методов обратной функции, метода исключения Неймана и их достоинства и недостатки?

Практическое занятие № 6. Моделирование непрерывных случайных величин

Задание 1. Метод моделирования условий предельных теорем

Назначение – моделирование непрерывных случайных величин с заданным законом распределения путем приближенного воспроизведения условий, при которых оказываются справедливыми соответствующие предельные теоремы.

Область применения – только для тех случайных величин для которых в теории вероятности сформулированы предельные теоремы.

Методические рекомендации: Принцип действия метода проиллюстрируем на примере центральной предельной теоремы теории вероятностей. С помощью этой теоремы можно моделировать случайную величину с нормальным законом распределения.

Центральная предельная теорема. Пусть _1,₂,...,_n – взаимно независимые нормированные случайные величины с одним и тем же распределением. Тогда при n→∞ распределение нормированных сумм

(6.1)

стремится к нормальному распределению с плотностью вероятностей



Если в качестве независимых случайных величин _I использовать базовые случайные величины _i с математическим ожиданием М[] = 1/2 и дисперсией Д[] = 1/12, то нормированная сумма (6.1) примет вид

(6.2)

Методические рекомендации: Практическая реализация. По формуле (6.2) при достаточно больших n можно вычислить приближенное значение нормальной случайной величины  с параметрами:М[] = 0, D[] = 1.

Расчеты показали, что уже при n =12 можно получить достаточно хорошее приближение к нормальному распределению. Поэтому на практике для моделирования случайной величины с нормальным законом распределения используется выражение



Тогда нормально распределенную случайную величину с произвольно заданными значениями математического ожидания m и среднеквадратичного отклонения  можно моделировать по формуле

Функция плотности случайной величины _n имеет вид:

Задание 2. Метод композиции

Назначение – моделирование непрерывных случайных величин с достаточно сложными функциями распределения.

Область применения. Метод композиции используется в тех случаях, когда ни один из изученных ранее методов в отдельности не приводит к желаемым результатам, но однако закон распределения моделируемой случайной величины можно представить в виде линейной комбинации нескольких известных законов распределения.

Методические рекомендации: Пусть функция распределения F(x) случайной величины  представлена в виде: 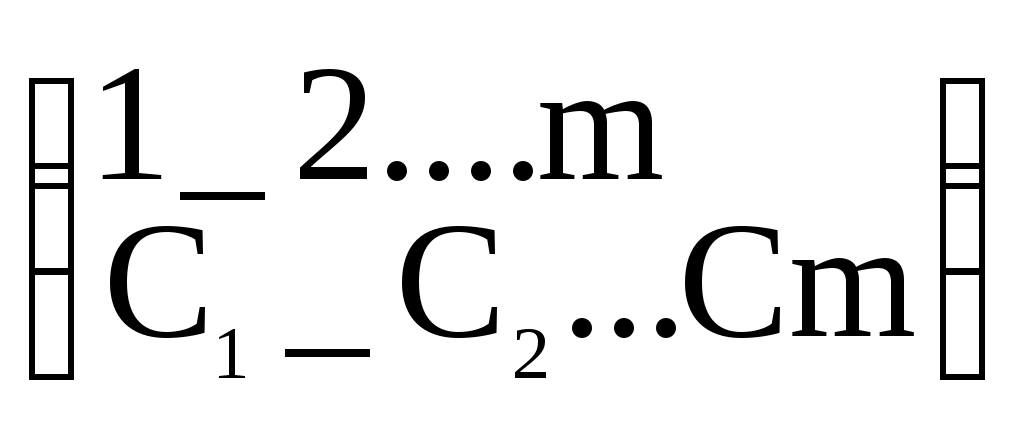где все F_k(x) – известные функции распределения, а параметры С_к удовлетворяют условиям C_k>0 и . Следовательно можно ввести дискретную случайную величину  с распределением



так, что Р(=к) = С_к.

Теорема. Пусть ₁ и ₂ – независимые базовые случайные величины. Если по ₁ разыграть значение =к случайной величины , а затем из уравнения F_k() = ₂ определить  то функция распределения  есть F(x).

Методические рекомендации: Практическая реализация заключается в следующем. Метод преобразует моделируемое сложное распределение к виду, удобному для формирования отдельных реализаций  одним из известных методов моделирования.

Алгоритм моделирования может быть представлен в виде следующей последовательности шагов:

Шаг 1. Единичная площадь под функцией плотности f(x) делится на m частей, каждая из которых имеет площадь С_к и соответствует f_k(x).

Шаг 2. С помощью ₁ моделируется дискретная случайная величина . Полученная реализация (допустим =к) определяет номер слагаемого F_k(x), которое будет использовано для выработки очередной реализации искомой случайной величины .

Шаг 3. Одним из известных методов, например, методом обратной функции, вырабатывается очередная реализация x_i случайной величины .

Затем шаги повторяются до тех пор, пока не будет получено требуемое количество значений непрерывной случайной величины .

Просчитать численный пример для следующих значений методом исключения Неймана при графическом задании функции плотности:

N=4, A=1, B=7, M=4, K=4, T(1)=1.25, T(2)=3, T(3)=2.5, T(4)=2, T(5)=1.75, T(6)=1.9, T(7)=3.5. . Составить блок-схему алгоритма метода исключения Неймана.

Основная литература: 5,9

Контрольные вопросы:

1. . Решить методом исключения Неймана.

2. Идея метода предельных теорем?
Практическое занятие № 7. Моделирование потоков событий

Задание 1. Моделирование простейшего потока

Определение. Поток называется простейшим если он обладает свойствами: стационарности, ординарности и отсутствия последствия.

Характеристики потока. Интервалы между событиями являются случайными величинами с показательным законом распределения: . В силу свойства отсутствия последствия

Методические рекомендации: Алгоритм моделирования простейшего потока состоит из трех шагов:

Шаг 1. Моделирование реализации Z базовой случайной величины .

Шаг 2. Определение реализации случайной x интервала между событиями потока  методом обратной функции.

Шаг 3. вычисление момента появления событий по формуле (6.2).

Задание 2. Моделирование потока Пальма

Определение. Однородный поток, обладающий свойствами стационарности, ординарности и ограниченного последствия, называется потоком Пальма.

Характеристика потока. Интервалы между событиями потока являются случайными величинами с заданной функцией плотности f(x) .

Для этого потока справедливо отношение

f₁(x₁)≠f₂(x₂)= f₃(x₃)=…= f_n(x_n)=f(x).

Методические рекомендации: Алгоритм моделирования потока Пальма состоит из следующих шагов:

Шаг 1. По формуле Пальма находится функция плотности f₁(x₁).

Шаг 2. Определяется реализация x₁ случайной величины₁ с функцией плотности f₁(x₁).

Шаг 3. Определяются реализации x_i (i=2,3,…,n) случайной величины  с функцией плотности f(x).

Шаг 4. Моменты появления событий потока вычисляются по формуле (4.2).

Пример.

Рассмотрим поток Пальма с равномерным законом распределения интервалов между событиями, т. е.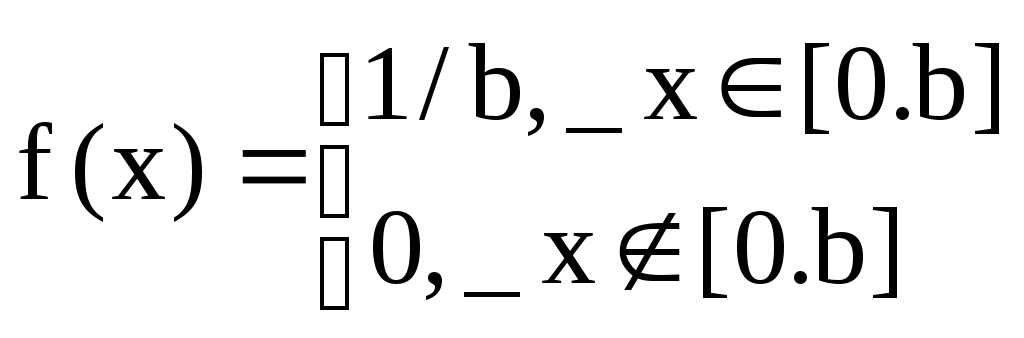



Шаг 3. Остальные значения x_i (i=2, 3, …, n) могут быть получены очевидным преобразованием X_i=b Z_i

Шаг 4. Моменты появления событий легко находятся по формуле

T_j =T_J-1+X_i, i=1, 2, … n ; j=1, 2, … n ;

Задание 3. Моделирование потоков Эрланга

Определение. Потокам Эрланга к-го порядка называется поток, получающийся из простейшего потока путем сохранения каждого k-го события и отбрасывания остальных.

Характеристики потока. Математическое ожидание, дисперсия и среднеквадратическое отклонение для потока Э_к имеет вид:

м_k=k/ λ; D_k=k/ λ²; σ_k= .

Интенсивность потока Эрланга определяется формулой

Λ_к= λ/к.

Здесь λ – это интенсивность простейшего потока

Методические рекомендации: Практическая реализация потока Эрланга k -го порядка осуществляется следующим образом. Очередное значение случайной величины n_i(i>1) получается как сумма к независимых случайных чисел, экспоненциальное распределение: , i>1, где τ_j–случайные величины с экспоненциальным распределением.

Тогда t_i = t_i-1+η_i, i=1, 2, …n, .

Изучите моделирование потоков событий.Составить блок-схему алгоритма моделирования стационарного, ординарного потока с ограниченным последействием. Составьте блок-схему алгоритма моделирования потока Эрланга. Составить блок-схему алгоритма моделирования простейшего потока.

Основная литература: 5,9

Контрольные вопросы:

1.Определить вероятность того, что в течение 30 минут появится ровно 5 событий простейшего потока с интенсивностью =0.2.

2.Определить значение интервала между соседними событиями простейшего потока с интенсивностью  и вычислить момент появления j-го события простейшего потока.

3.Получите выражения для , а затем формулу для нахождения х₁, если , =0.3.

4.Составьте блок-схему алгоритма моделирования потока Пальма с равномерным законом распределения. Для выработки базовой последовательности используйте метод вычетов.

5.Вычислить по заданной функции плотности f(x) математическое ожидание интервалов _j , j>1, определить интенсивность потока Пальма и определить моменты появления события потока.

6.Определить интенсивность потока Эрланга 5-го порядка, если для простейшего потока =0.15.

7.Вычисть длину интервала между событиями потока и момент появления события для следующих значений: n=5, k=3, d=405, Z₀=117, c=6985, m=32787, t0=0, h=0.25.

8.Что такое поток?

9. Что такое поток Эрланга k-го порядка?

10. Какими свойствами обладают потоки?
2.4 Планы лабораторных занятий.

Лабораторная работа № 1 Моделирование базовой последовательности

Цель работы – изучение методов базовой последовательности.

Задание. Запустить файл TP7\turbo.exe\Lab 1. Выбрать соответствующий метод.

По методу усечения необходимо реализовать два алгоритма: середины квадратов и середины произведения.

С помощью алгоритма середины квадратов необходимо

а) получить зацикливание (0,6100; 0,4100; 0,2100; 0,8100) и зафиксировать z[0], z[1] и порядковый номер элемента, с которого начинается зацикливание;

б) добиться вырождения последовательности к нулю или любой другой константе и также зафиксировать z[0], z[1] и порядковый номер элемента, с которого начинается вырождение.

С помощью алгоритма середины квадратов для исходных данных z[0], z[1], полученных в пунктах а) и б), необходимо определить длину отрезка апериодичности.

Для алгоритмов метода вычетов необходимо подобрать такие исходные значения параметров, с которыми нужно добиться максимального возможных значений периода последовательности равного m для полного и m/4 для неполного алгоритмов.

Основная литература:6,10

Лабораторная работа № 2. Моделирование базовой последовательности

Задание. Метод суммирования. Для моделирования базовой последовательности по алгоритму Фибоначчи используйте начальные значения z[0], z[1] пункта а) метода усечения. А для реализации аддитивного алгоритма – элементы z[0], z[10] последовательности Фибоначчи.

Определите длину интервала апериодичности для этих последовательностей и сравните между собой.

Основная литература: 6,10

Лабораторная работа № 3. Моделирование случайных событий

Цель работы – приобретение навыков моделирования на ПЭВМ случайных событий.