имитнов2008. Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности
 Скачать 1.61 Mb.
|
Схема алгоритмов модели.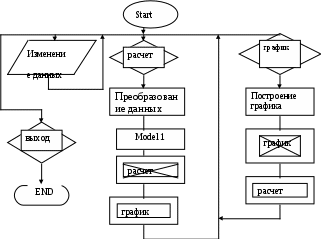 Схема алгоритма процедур обработки прерываний показана на рисунке 17. После подачи команды Start на экране появляется активная стартовая форма. С этого момента программа находится в режиме ожидания действия пользователя.Рисунок 17-Схема алгоритма процедур обработки прерываний Цифрой 1 на схеме обозначено действие пользователя, которое заключается в корректировке исходных данных. Измененные данные вводятся в соответствующие текстовые поля. При этом фиксируются в памяти не как числа, а как значения символьных переменных. Цифрой 2 на схеме обозначено действие пользователя, которое заключается в нажатии командной кнопки «Расчет». В результате этого вызывается одна из так называемых процедур прерываний. Внутри этой процедуры оператор 3 производит преобразование символьных данных в числовые. Затем оператор 4 обращается к программному модулю общего назначения «Мodel 1», который производит расчет массива значений цен как функций времени. После окончания работы программного модуля оператор 5 делает кнопку «Расчет» неактивной, а оператор 6 активизирует кнопку «График». Одновременно производится очистка части стартовой формы, которая отведена для построения графика. Цифрой 7 на схеме обозначено действие пользователя, которое заключается в нажатии кнопки «График».В результате группа операторов 8 обеспечивает построение в центре стартовой формы графика зависимости текущей цены н продукт от времени. Затем оператор 9 делает кнопку «График» неактивной, а оператор 10 вновь активизирует кнопку «Расчет». Числом 11 на схеме обозначено действие пользователя, которое заключается в нажатии кнопки «Выход». В этом случае работа программы заканчивается. Схема алгоритма модуля «Model 1» показана на рисунке 18. Внутри этого модуля группа операторов 1 определяет цены для 1-го и 2-го отрезков времени по формулам (14), (15). Оператор 2 является началом циклического перебора временных отрезков, начиная с 3-го и кончая последним ТК-М. Группа операторов 3 вырабатывает три возможных значения эталонной случайной величины с нормальным распределением, которые используются группой операторов 4 для расчета возможных значений случайных переменных UТ ,VТ, WТ с заданным СКО. Оператор 5 осуществляет расчет выходной переменной РТ по формуле (13) . Оператор 6 подготавливает новые значения переменных PT-1 и РТ-2 для расчета Рт на следующем временном отрезке (следующем витке цикла). 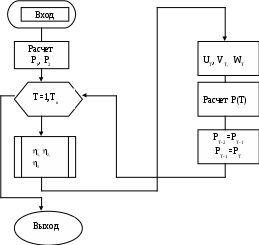 Рисунок 18 - Схема алгоритма модуля «Моdel» Модель бензоколонки.Задача моделирования. Предприниматель хочет вложить деньги в строительство новой бензоколонки. Однако точного представления о том, сколько автомашин будет ежедневно заправляться на той колонке. Какова должна быть оптимальная структура бензоколонки и на получение какой прибыли он может рассчитывать? Нужно выбрать математическую схему, которая ближе всего подходит к такой экономической системе, как бензоколонка. Математической схемой является схема системы массового обслуживания. Для таких систем характерны три отличительные особенности: 1) имеется поток клиентов, желающих быть обслуженными (в данном случае это поток автомашин, желающих заправиться бензином); 2) имеются устройства или агрегаты, которые обеспечивают удовлетворение заявок клиентов (в данном случае одна или несколько раздаточных колонок); имеется определенный набор правил обслуживания клиентов (т.е.никто не имеет права на заправку вне очереди). Пусть имеется система массового обслуживания с переменным числом каналов Nk, которое может принимать любое значение в диапазоне от одного до трех. Входной поток заявок – простейший, следовательно, время между соседними заявками имеет показательное распределение с известным математическим ожиданием (средним значением) Тз.ср. Время обслуживания заявки в любом канале – величина случайная, имеющая показательное распределение с известным средним временем обслуживания Тобс.ср. Все заявки однородны и независимы. Правило обслуживания состоит в том, что очередная заявка поступает в тот канал, который раньше других освободился. Если время ожидания начала обслуживания превышает заданную величину Тож.max , то заявка покидает систему не обслуженной. Период функционирования СМО характеризуется величиной Ткон. Таким образом входными характеристиками модели являются: число каналов Nk , среднее время между соседними заявками Тз.ср, среднее время обслуживания заявки Тобс.ср., максимально допустимое время ожидания Тож.max, период работы системы Ткон , число случайных реализаций моделируемого процесса Nр. Выходной характеристикой модели является среднее число обслуженных заявок Nобс.ср. Выбор показателя и критерия эффективности В качестве показателя эффективности работы системы целесообразно выбрать среднюю прибыль, определяемую по формуле  , (16)где  - чистая прибыль, полученная в результате обслуживания одной заявки; - издержки обслуживания всех заявок, зависящие от числа каналов.Разделим обе части равенства (5..5) на величину . Получим следующее выражение для расчета показателя эффективности: (17)где  - средняя относительная прибыль.Величину  (отношение издержек обслуживания к чистой прибыли, полученной в результате обслуживания одной заявки) будем рассматривать как функцию числа каналов.Предположив, что возможными вариантами этой функциональной зависимости являются: a– линейная зависимость; б- возрастающая зависимость с положительной 2-й производной и в-возрастающая зависимость с отрицательной 2-й производной (рисунок 19). 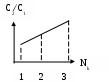 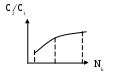 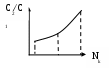 1 2 3 1 2 3 а b в Рисунок 19 - Зависимости отношения C2/C1 от Nk а –первый вариант; б -второй вариант; в -третий вариант. Выберем второй вариант. Примем в качестве конкретной зависимости издержек обслуживания от числа каналов следующую функцию:  (18)Итак, для расчета показателя эффективности будем использовать зависимости (16) и (17). В качестве критерия выбора наивыгоднейшей структуры СМО примем оптимальное число каналов, обеспечивающее максимум средней относительной прибыли:  (19)где  -наивыгоднейшее число каналов.Схемы алгоритмов модели О 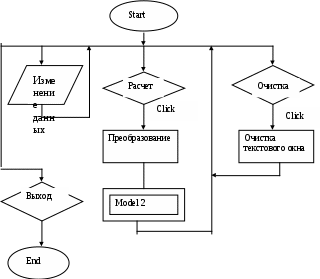 бщий вид стартовой формы показан на рисунке 20. Видно, что она включает ряд объектов управления, среди которых имеются три командные кнопки: «Расчет», «Очистка» и «Выход».Click Рисунок 20 - Схема алгоритма процедур обработки прерываний После нажатия кнопки «Start» активизируется стартовая форма. С этого момента программа находится в режиме ожидания действий пользователя. Цифрой 1 обозначено действие, заключающееся в корректировке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля. Цифрой 2 обозначено действие, заключающееся в нажатии кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Моdel2». Схема алгоритма этого модуля приведена на рисунке 21. После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Цифрой 5 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Очистка» В процедуре, связанной с ней, производится очищение текстового поля для вывода результата моделирования. Затем обычно производятся изменение исходных данных и проведение новых расчетов с использованием кнопки «Расчет». Цифрой 7 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Выход». В результате работа программы прекращается. Оператор 1обнуляет глобальную переменную SNобс - суммарное число обслуженных заявок. Оператор 2 активизирует окно формы № 2 и делает неактивным окно формы № 1. оператор 3 начинает циклический перебор случайных реализаций. Оператор 4 выводит на экран счетчик числа рассчитанных реализаций. Оператор 5 в начале каждой случайной реализации обнуляет локальные переменные, к которым относятся: число заявок, поступающих в одной реализации NZ , число обслуженных заявок в каждом из трех каналов Nобс.1, Nобс.2, Nобс.3, начальные значения времени освобождения 1-го, 2-го и 3-го каналов ТОК1 , ТОК2 и ТОК3.. Оператор 6 обращается к автономной процедуре формирования потока заявок. В результате работы этой процедуры формируется массив значений времени[ТЗ (1), ТЗ (2), ТЗ (3),…, ТЗ (Nзi)] где Nзi – общее число поступивших заявок для i-й случайной реализации. Оператор 7 является началом цикла обслуживания заявок. Оператор 8, 9, 10 и 11 производят выбор номера канала, который характеризуется наименьшим значением времени освобождения от обслуживания заявки. Оператор 12 обращается к автономной процедуре обслуживания очередной заявки. На выходе этой процедуры определяется число обслуженных заявок в выбранном канале Nобс(Jmin). Оператор 13 служит для расчета суммарного числа обслуженных заявок по рекурсивной формуле  .После окончания цикла случайных реализаций оператор 14 возвращает свойство активного окна форме № 1. Оператор 15 рассчитывает и выводит н экран значение выходной переменной - средней относительной прибыли по формуле  Основная литература: 1 [55-111] Контрольные вопросы 1. Какие виды модели существуют ? 2. По какой формуле рассчитывается показатель эффективности? Чему равно число каналов в модели бензоколонки? Тема лекции № 6. Моделирование процессов и систем управления. Модель производственной фирмы. Имеется производственная фирма, которая осуществляет выпуск сложных изделий по заказам потребителей. Технологический процесс предусматривает изготовление отдельных узлов и агрегатов с помощью различного оборудования, которое может размещаться в нескольких цехах. Количество цехов Nц - величина переменная, изменяющаяся от 1 до 4. Поток заказов - простейший (пуассоновский) с известным средним числом заказов в день - Lz. Случайная величина времени изготовления одного изделия складывается из случайных величин времени изготовления агрегатов в каждом цехе, имеющих нормальное распределение. Среднее значение времени работы (времени «обслуживания» изделия) в j-м цехе Tоб.jдля каждого варианта структуры предприятия считается заданным. Суммарное среднее время изготовления изделия TSявляется постоянным. Разброс времени работы в каждом цехе характеризуется относительным средним квадратическим отклонением  , постоянным для всех цехов. На выпуск продукции оказывает влияние структура предприятия, т. е. количество цехов и распределение ресурсов по цехам. Число возможных вариантов структуры бесконечно. Поэтому для исследования влияния структуры фирмы на эффективность производственного процесса необходимо выбрать параметр или числовой фактор, который свел бы количество расчетных вариантов к обозримому числу. В качестве такого числового фактора предлагается ввести следующее выражение: Fact= {MAX(Tоб.j) – MIN(Tоб.j)} / TS(.j=1, 2, 3, 4), где MAX(Tоб.j) - максимальное среднее время работы для различных цехов; MIN(Tоб.j) - минимальное среднее время работы для различных цехов; TS- суммарное среднее время изготовления изделия. Чистая прибыль, получаемая в результате изготовления одного изделия, равна %Р. Дополнительные затраты фирмы на обеспечение производства за период TDдней равны $С. Поэтому случайная прибыль определяется по формуле Prof=NиздP-C, где Nизд- количество выпущенных изделий для одной случайной реализации моделируемого процесса. В качестве показателя эффективности исследуемой системы принята минимальная гарантированная прибыль, определяемая по формуле Gprof=Mprof= K   prof,где Mprof - математическое ожидание прибыли; prof, - среднее квадратическое отклонение прибыли; Ка - квантиль нормального распределения, соответствующий заданному уровню надежности а (Ка=1,28 при а=0,9). Управляющими (варьируемыми) параметрами модели являются: массив среднего времени «обслуживания» изделий в цехах, используемый для расчета значения числового фактора; относительная величина разброса времени работы в каждом цехе .В качестве критерия эффективности принят максимум минимальной гарантированной прибыли K(Fact*) : MAX {Gprof (Fact)}, где Fact* - оптимальное значение числового фактора. Схемы алгоритма модели. Схема алгоритма модели показана на рисунке 21. |