имитнов2008. Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
Вопросы для подготовки к промежуточной аттестацииОсновные понятия имитационного моделирования. Процесс имитационного моделирования. Методологические подходы имитационного моделирования. Дискретное имитационное моделирование. Непрерывное имитационное моделирование. Комбинированное имитационное моделирование. Основы алгоритмического статистического моделирования. Классификация математических моделей экономических систем. Типовые математические схемы. 10.Способ повременного моделирования с постоянным шагом 11.Повременное моделирование с переменными шагом. 12.Последовательная проверка заявок. 13.Поэтапная последовательная проводка заявок 14.Общая структура моделируемого алгоритма. 15.Регенеративный метод анализа 16.Планирование эксперимента. 17.Паутинообразная модель фирмы. 18.Модель производственной фирмы. 19.Модель бензоколонки. 20.Модель управления запасами. 21.Модель торговой точки. 1.9 Требования Обязательное посещение лекционных занятий. В случае, если по какой-либо причине, вы не можете посещать занятия, вы будете изучать пропущенный материал самостоятельно. По темам лекционного курса проводятся 2 рубежных контроля в виде письменной работы, на которых проверяются теоретическая часть материала . Посещение практических и лабораторных занятий, а также активное участие в обсуждении будут сопровождаться процентами (более 20% ) Выполнение всех требований обеспечивает допуск к экзамену. содержание Активного раздаточного материала 2.1 Тематический план курса Распределение часов по видам занятий
2.2 Конспект лекционных занятий Тема лекции №1. Введение в имитационное моделирование. Проблемы, с которыми приходится сталкивается в различных сферах нашей жизни, постоянно усложняются. Это определяет необходимость совершенствования имеющихся и разработки новых методов и процедур их решения. Имитационное моделирование является эффективным средством решения сложных проблем. Имитационные модели могут применяться для: исследования границ и структур систем с целью решения конкретных проблем; определения и анализа критических элементов, компонентов и точек в исследуемых системах и процессах; синтеза и оценки предполагаемых решений; прогнозирования и планирования будущего развития исследуемых систем. Процесс имитационного моделирования начинается с определения подлежащих решению проблем, что в свою очередь определяет состав и границы исследуемой системы. Модель –это описание системы. В физических науках модели обычно разрабатываются на основе теоретических законов и принципов. Моделями могут быть масштабированные физические объекты, математические уравнения и взаимосвязи. Модели эффективно используются, в частности, при описании, проектировании и анализе систем. Разработка модели – сложный процесс, который во многом является искусством, но, однако, упрощаются, если: 1) известны физические законы, описывающие функционирование системы; 2) может быть разработано графическое представление системы; 3) можно управлять входами, элементами и выходами системы. Построение моделей. Модель представляет собой абстрактное описание системы, уровень детализации которого определяет сам исследователь. Человек принимает решение о том, является ли данный элемент системы существенным, а следовательно, будет ли он включен в описание системы. Это решение принимается с учетом цели, лежащей в основе разработки модели. От того, насколько хорошо исследователь умеет выделять существенные элементы и взаимосвязи между ними, зависит успех моделирования. На рисунке 1 приведена схема предлагаемого подхода к построению моделей. Система рассматривается как состоящая из множества взаимосвязанных элементов, объединенных для выполнения определенной функции. Определение системы во многом субъективно, т.е. оно зависит не только от цели разработки модели, но и от того, кто именно определяет систему 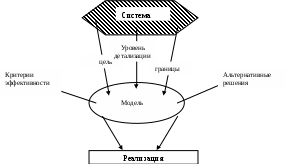 Рисунок 1 - Процесс построения модели Итак, процесс моделирования начинается с определения цели разработки модели, на основе которой затем устанавливается границы системы и необходимый уровень детализации моделируемых процессов. Выбранный уровень детализации должен позволять абстрагироваться от неточно определенных из-за недостатка информации аспектов функционирования реальной системы. В описание системы, кроме того, должны быть включены критерии эффективности функционирования системы и оцениваемые альтернативные решения, которые могут рассматриваться как часть модели или как ее входы. Оценка альтернативных решений по заданным критериям эффективности рассматриваются как выходы модели. Обычно оценка альтернатив требует внесения изменений в описание системы и, следовательно, перестройки модели. После того как на основе полученных оценок альтернатив могут быть выработаны рекомендации, можно приступать к внедрению результатов моделирования. При этом в рекомендациях должны быть четко сформулированы как основные решения, так и условия их реализации. Имитационные модели. Имитационной моделью будем называть логико-математическое описание системы, которое может быть исследовано в ходе проведения экспериментов на ПЭВМ и, следовательно, может считаться лабораторной версией системы. После окончания разработки имитационной модели с ней проводятся машинные эксперименты, которые позволяют сделать выводы о поведении системы: без ее построения, если это проектируемая система; без вмещательства в ее функционирование, если это действующая система, экспериментирование с которой или слишком дорого, или небезопастно; без ее разрушения, цель эксперимента состоит в определении пределов воздействия на систему. Таким образом, имитационные модели могут использоваться для проектирования , анализа и оценки функционирования систем. В настоящее время имитационное моделирование используется для исследования разнообразных систем, в частности городских, экономических, коммерческих, производственных, биологических, социальных, транспортных систем и другие. Имитационное моделирование – это представление динамического поведения системы посредством продвижения ее от одного состояния к другому в соответствии с хорошо определенными операционными правилами. Изменения состояния системы могут происходить либо непрерывно, либо в дискретные моменты времени. Хотя процедура описания динамического поведения дискретно и непрерывно изменяющихся моделей различны, основная концепция имитации системы –отображение изменений ее состояния с течением времени – остается той же. Процесс имитационного моделирования. Процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с требованиями, предъявляемыми решаемой проблемой. В процессе имитационного моделирования можно выделить следующие основные этапы: 1.Формулирование проблемы; описание исследуемой проблемы и определение целей исследования. 2.Разработка модели: логико-математическое описание моделируемой системы в соответствии с формулировкой проблемы. 3.Подготовка данных: идентификация, спецификация и сбор данных. 4.Трансляция модели: перевод модели на язык, приемлемый для используемой ПЭВМ. 5.Верификация: установление правильности машинных программ. 6.Валидация: оценка требуемой точности и соответствия имитационной модели реальной системе. 7.Стратегическое и тактическое планирование: определение условий проведения машинного эксперимента с имитационной моделью. 8. Экспериментирование: прогон имитационной модели на ПЭВМ для получения требуемой информации. 9. Анализ результатов: изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы. 10.Реализация и документирования: реализация рекомендаций , полученных на основе имитации, и составление документации по модели и ее использованию. Основная литература: 2 [ 11-23] Дополнительная литература: 7.[11-25] Контрольные вопросы Что такое модель? Что такое имитационное моделирование? Где используются имитационные модели? Перечислить этапы построения имитационного моделирования? Тема лекции № 2.Методологические подходы в имитационном моделировании. Системы и модели. Система – это совокупность элементов, которые принадлежат ограниченной части реального мира, являющейся объектом исследования. Поэтому система относительное. В одном случае некоторая совокупность элементов может рассматриваться только как небольшая часть большой системы, т.е. в качестве подсистемы, а в другом та же совокупность может быть в центре интересов исследователя, т.е. рассматриваться как система. Сфера действия любой системы и любой модели системы однозначно определяется целью, для достижения которой он выделяется и идентифицируется. Сфера действия любой имитационной модели определяется также особенностями той проблемы, для решения которой разрабатывается эта модель. Для установления сферы действиям системы исследовать должен выявить ее границы и состав. При установлении границ системы выявляются не только физические, но и причинно-следственные взаимосвязи между ее элементами. На систему, которой дано предварительное определение, могут воздействовать некоторые внешние факторы. Если существенно влияют на поведение системы, экспериментировать с такой системой не имеет смысла, и ее следует, переопределить. Если внешние факторы частично воздействуют на систему, существуют следующие возможности: расширить определение системы, включив в него эти факторы; пренебречь этими факторами; трактовать их как входы в систему. Если внешние факторы трактуются как входы в систему, предполагается, что они функционально задаются с помощью предписанных значений, таблиц или уравнений. Например, когда разрабатывается модель производственной системы (рисунок 2)   Рисунок 2 – Модель производственной системы в условиях внешних воздействий Фирмы и сбыт производимого этой фирмой изделия рассматривается как вход в производственную систему, в модель не включаются причинно-следственные взаимосвязи, относящиеся к процессу сбыта. Такая модель будет содержать только статистическое описание предшествующих и предполагаемых продаж, используемое в качестве входа, т.е. организация сбыта находится за границами моделируемой системы. В системной терминологии объекты. Которые находятся за границами системы, но могут влиять на ее поведение, формируют окружающую среду этой системы. Таким образом, системы представляют собой совокупность взаимодействующих элементов, которые подвергаются воздействию со стороны внешних факторов. Модели систем классифицируются на дискретно и непрерывно изменяющиеся. Практически одну и ту же систему можно представить в виде дискретно изменяющейся (дискретной) модели либо непрерывно изменяющейся (непрерывной). В имитационном моделировании время является основной независимой переменной. Другие переменные, включенные в имитационную модель, являются функциями времени, т.е. зависимыми переменными. При дискретной имитации зависимые переменные изменяются дискретно в определенные моменты имитационного времени, называемые моментами свершения событий. Переменная времени в имитационной модели может быть либо непрерывной, либо дискретной в зависимости от того, могут ли дискретные изменения зависимых переменных происходить в любые моменты времени или только в определенные моменты.(рисунок 3)  Рисунок 3 - Графическое представление отклика дискретно-событийного имитатора При непрерывной имитации зависимые переменные модели изменяются непрерывно в течение имитационного времени. Непрерывная модель может быть может быть либо непрерывной (рисунок 4) либо дискретной по времени (рисунок 5) в зависимости от того, будут ли значения зависимых переменных доступны в любой точке или только в определенные моменты имитационного времени. 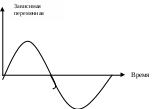  Рисунок 4 - Графическое представление отклика непрерывного имитатора 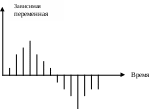 Рисунок 5 - Графическое представление отклика непрерывного имитатора с дискретным временем При комбинированной имитации зависимые переменные модели могут изменяться дискретно, непрерывно или непрерывно с наложенными дискретными скачками. Время изменяется либо дискретно, либо непрерывно. Наиболее важный аспект комбинированной имитации заключается в возможности взаимодействий между дискретно и непрерывно изменяющимися переменными.(рис.6)   Рисунок 6 - Графическое представление отклика комбинированного имитатора Дискретное имитационное моделирование Элементы дискретных систем, такие, как люди, оборудования, заказы, потоки материалов и т.п. включенные в имитационную модель, будем называть ее компонентами. Существует много типов компонентов, каждый из которых описывается различными характеристиками. Компоненты, участвующие в действиях различного типа, могут иметь одну или несколько общих характеристик, что позволяет объединять их в группы. Группы компонентов называются файлами. Целью дискретного имитационного моделирования является воспроизведение взаимодействий, в которых участвуют компоненты, и изучение поведения и функциональных возможностей исследуемой системы. Для этого выделяются состояния системы и описываются действия, которые переводят ее из одного состояния в другое. Говорят, что система находится в определенном состоянии, когда все ее компоненты находятся в состояниях, совместимых с областью значений, описывающих это состояние характеристик. Таким образом, имитация – это динамический «портрет» состояний системы во времени, т.е. воспроизведение поведения системы во времени. П 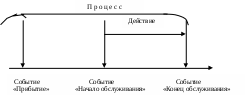 ри дискретной имитации состояние системы может меняться только в моменты свершения событий. Так как состояние системы не изменяется между этими моментами, полный динамический портрет состояний системы может быть получен путем продвижения имитационного времени от одного события к другому. Функционирование дискретной имитационной модели можно задать следующим образом: определяя изменения состояния системы, происходящие в момент свершения событий; описывая действия, в которых принимают участие элементы системы, или процесс, через который проходят элементы. Взаимосвязь между понятиями событие, действие и процесс представлены на рисунке 7. ри дискретной имитации состояние системы может меняться только в моменты свершения событий. Так как состояние системы не изменяется между этими моментами, полный динамический портрет состояний системы может быть получен путем продвижения имитационного времени от одного события к другому. Функционирование дискретной имитационной модели можно задать следующим образом: определяя изменения состояния системы, происходящие в момент свершения событий; описывая действия, в которых принимают участие элементы системы, или процесс, через который проходят элементы. Взаимосвязь между понятиями событие, действие и процесс представлены на рисунке 7. Время Рисунок 7 - Взаимосвязь между событиями, действиями и процессами Событие происходит в тот момент, когда принимается решение о начале или окончании действия. Процесс – это ориентированная во времени последовательность событий, которая может состоять из нескольких действий. Эти представления лежат в основе трех альтернативных методологических подходов к построению дискретных имитационных моделей, называемых обычно событийным подходом, подходом сканирования активностей и процессно-ориентированным подходом. Событий подход. При событийном подходе система моделируется путем идентификации изменений, происходящих в ней в моменты свершения событий. Задача исследователя заключается в описании событий, которые могут изменить состояние системы, и определении логических взаимосвязей между ними. Имитация функционирования системы осуществляется путем выполнения упорядоченной во времени последовательности логически взаимосвязанных событий. Для иллюстрации событийного подхода вновь рассмотрим пример банка с одним кассиром. Клиенты заходят в банк, после возможного ожидания обслуживаются кассиром и затем уходят. Состояние системы в этом примере определяется состоянием кассира и числом ожидающих обслуживания клиентов. Оно остается неизменным, за исключением моментов, когда клиент прибывает в систему или покидает ее. Поэтому событийная модель в данном случае состоит из описания действия, происходящихся в момент прибытия и окончания обслуживания очередного клиента. Так как изменения состояния системы могут происходить только в эти моменты времени, использование событий «прибытие» и «конец обслуживания» полностью обеспечивает воспроизведение динамики функционирования системы. Обсудим сначала логику события «прибытие». Операторная схема этого события имеет следующий вид: Планирование следующего прибытия. Если кассир занят: число ожидающих=число ожидающих = число ожидающих+1; Возврат. Если кассир свободен: перевод кассира в состояние «занят»; Планирование события «окончание» обслуживания в момент времени = текущее время+время обслуживания; возврат. Конец. На первом планируется прибытие следующего клиента, что входе имитации при неоднократном обращении к этой процедуре позволяет организовать непрерывный поток прибытий. Поведение прибывшего клиента зависит от состояния системы в текущий момент времени. Если кассир занят, прибывший клиент становится в очередь. И изменение состояния системы осуществляется путем увеличения числа ожидающих клиентов на единицу. Если кассир свободен, прибывший клиент сразу же обслуживается, и изменение состояния системы осуществляется путем перехода в состояние «занят». Кроме того, должно быть запланировано событие «конец обслуживания» для данного клиента в момент времени, равный текущему времени плюс время, затрачиваемое кассиром на обслуживание. Рассмотрим логику обработки события «конец обслуживания». Операторная схема этого события имеет следующий вид: Если число ожидающих больше нуля; число ожидающих = число ожидающих –1; Планирование окончания обслуживания в момент времени, равный текущему времени+время обслуживания; Возврат. Если число ожидающих равно нулю: перевод кассира в состояние «свободен»; Возврат. Конец. Кассир заканчивает обслуживание очередного клиент, сначала проверяем, есть ли клиенты, ожидающие обслуживания. Если такие клиенты есть, их число уменьшается на единицу и планируется событие «конец обслуживания» первого из ожидающих клиентов. В противном случае кассир переходит в состояние «свободен». При имитации функционирования банка с одним кассиром на основе использования событийного подхода мы должны воспроизвести хронологию (календарь) событий и причины, вызывающие их появление в соответствующие моменты имитационного времени. Календарь событий первоначально содержит отметку только о первом событии «прибытие». В ходе имитации возникновение других событий «прибытие» и «конец обслуживания» должно быть запланировано в календаре в соответствии с логикой функционирования системы. События выполняются в упорядоченной по времени последовательности, при этом имитационное время продвигается от одного события к другому. Подход сканирования активностей. При использовании похода сканирования активностей разработчик описывает действия, в которых принимают участие элементы системы, и задает условия, определяющие начало и окончание этих действий. События, которые начинают или завершают действие, не планируются разработчиком модели, а инициируются по условиям, определенным для данного действия. Условия начала или окончания действия проверяются после очередного продвижения имитационного времени. Если заданные условия удовлетворяются, происходит соответствующее действие. Для того, чтобы было выполнено каждое действие в модели, сканирование условий производится для всего множества действий при каждом продвижении имитационного времени. Подход сканирования активностей обеспечивает простую схему моделирования для решения целого ряда проблем. Он наиболее эффективен для ситуаций, в которых продолжительность действия определяется в зависимости от того, насколько состояние системы удовлетворяет заданным условиям. Тем не менее, так как необходимо сканировать условия для каждого действия, подход сканирования активностей менее эффективен по сравнению с событийным походом и поэтому имеет ограниченное применение в дискретной имитации. Процессно-ориентированный подход. Имитационные языки, включающие операторы для моделирования процесса прохождения элементов через систему, обычно называются процессно-ориентированными. Эти операторы определяют последовательность событий, которые автоматически выполняются имитационным языком, по мере того элементы продвигаются через систему. Например, следующий набор операторов может быть использован для описания процесса в модели банка: Создавать прибывающих клиентов через каждые Т единиц времени; Ожидать кассира; Продвинуть время на продолжительность обслуживания; Освободить кассира; Удалить кассира; Первый оператор генерирует прибывающих в систему клиентов через каждые Т единиц имитационного времени. Величина Т может быть константой или принимать случайные значения. Оператор «ожидать» определяет, что клиент ожидает до тех пор, пока кассир освободится. Этот тип оператора аналогичен понятию действия по условию, применяемого в подходе сканирования активностей. Оператор «продвинуть время» моделирует тот период времени, в течение которого клиент обслуживался кассиром. Этот тип оператора аналогичен оператору планирования в событийном подходе. Он помещает в календарь событий метку о том, что обслуживание клиента будет закончено в момент, равный текущему имитационному времени плюс время обслуживания. После завершения обслуживания клиент покидает систему и кассир освобождается. Освобождение кассира позволяет сразу же приступить к обработке какого-либо ожидающего клиента из оператора «ожидать». Из приведенного примера видно, что процессно-ориентированный подход сочетает в себе черты событийного подхода и подхода сканирования активностей. Он обеспечивает описание прохождения компонентов через процесс, содержащий ресурсы. Простота этого подхода состоит в том, что определяемая операторами логика событий заложена в самом имитационном языке. Непрерывное имитационное моделирование. В непрерывной имитационной модели состояние системы представляется с помощью непрерывно изменяющихся зависимых переменных. Для того чтобы отличать непрерывно изменяющиеся переменные от дискретно изменяющихся, будем первые называть переменными состояния. Непрерывная имитационная модель создается путем задания уравнений для совокупности переменных состояния, динамическое поведение которых имитирует реальную систему. Модели непрерывных систем часто определяются в терминах производных переменных состояния. Это объясняется тем, что иногда легче задать выражение для определения скорости изменения переменной состояния, чем сделать это непосредственное для самой переменной. Уравнения такого вида, включающие производные переменных состояния, называют дифференциальными уравнениями. Пусть, например, в процессе разработки модели мы составили следующее дифференциальное уравнение для переменной состояния s по времени t: Первое уравнение определяет скорость изменения s как функцию от s и t , второе уравнение – начальное условие для переменной состояния. Цель имитационного эксперимента- определить реакцию переменной состояния в зависимости от имитационного времени. Комбинированные дискретно-непрерывные модели. В комбинированных дискретно-непрерывных моделях независимые переменные могут изменяться как дискретно, так и непрерывно. В рамках методологии комбинированного моделирования исследуемая система описывается с помощью элементов, их атрибутов и переменных состояния. Поведение системы имитируется путем вычисления значений переменных состояния через небольшие отрезки времени и значений атрибутов элементов в моменты свершения событий. В комбинированном моделировании применяются два типа событий: временные события(события, свершение которых планируется в определенные моменты времени) и события состояния (эти события не планируются, а происходят тогда когда система достигает определенного состояния). Например, как показано на рисунке 8 событие состояния произойдет, когда переменная состояния SS(1) пересечет переменную состояния SS(2) в положительном направлении. Отметим, что понятие «событие состояния» аналогично понятию «сканирование активностей», в котором событие также не планируется, а инициируется определенным состоянием системы. Возможность возникновения события состояния должна проверяться при каждом продвижении имитационного времени. 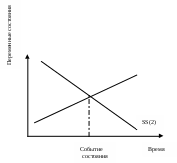 SS(1) Рисунок 8- Пример наступления события состояния Основная литература:2 [68-81] Дополнительная литература: 7 [26-35] Контрольные вопросы 1.Что такая система? 2.Что такое имитация? 3.Что такое дискретная, непрерывная и комбинированная имитация? Тема лекции № 3. Основы имитационного статистического моделированияПоследовательность разработки математических моделей. В процессе разработки и машинной реализации математической модели входят следующие этапы: Построение концептуальной модели; Разработка алгоритма модели системы; Разработка программы модели системы; Проведение машинных экспериментов с моделью системы. 1.Построение концептуальной модели Построение концептуальной модели включает следующие подэтапы Постановку задачи моделирования; Определение требований к исходной информации и ее сбор; Выдвижение гипотез и предположений; Определение параметров и переменных модели; Обоснование выбора показателей и критериев эффективности системы; Составление содержательного описания модели. При постановке задачи моделирования дается четкая формулировка целей и задач исследования реальной системы, обосновывается необходимость машинного моделирования, выбирается методика решения задачи с учетом имеющихся ресурсов, определяются возможность разделения задачи на подзадачи. При сборе необходимой исходной информации необходимо помнить, что именно от качества исходной информации необходимо помнить, что именно от качества исходной информации об объекте моделирования зависит как адекватность модели, так и достоверность результатов моделирования. Гипотезы при построении модели системы служат для заполнения «пробелов» в понимании задачи исследователем. Предположения дают возможность провести упрощение модели. В процессе работы с моделью системы возможно многократное возвращение к этому подэтапу в зависимости от полученных результатов моделирования и новой информации об объекте. При определении параметров и переменных составляется перечень входных, выходных и управляющих переменных, а также внешних и внутренних параметров системы. Выбранные показатели и критерии эффективности системы должны отражать цель функционирования системы и представлять собой функции переменных и параметров системы. Разработка концептуальной модели завершается составлением содержательного описания, которое используется как основной документ, характеризующей результаты работы на первом этапе. 2. Разработка алгоритма модели Разработка алгоритма модели включает следующие подэтапы: Построение логической схемы алгоритма; Получение математических соотношений; Проверку достоверности алгоритма Вначале создается укрупненная схема моделирующего алгоритма, которая задает общий порядок действий при моделировании исследуемого процесса. Затем разрабатывается детальная схема. Каждый элемент которой впоследствии превращается в оператор программы. Для комбинированных моделей разрабатывается аналитическая часть в виде явных функций и имитационная часть в виде моделирующего алгоритма. Проверка достоверности алгоритма должна дать ответ на вопрос, насколько алгоритм отражает замысел моделирования, сформулированный на этапе разработки концептуальной модели. 3 Разработка программы Разработка программы для ЭВМ включает следующие подэтапы: выбор вычислительных средств; проведение программирования; проверку достоверности программы. Прежде всего выбирается тип ЭВМ и язык программирования. Создание программы по детально разработанному алгоритму может осуществить программист без участия и помощи разработчика модели. После составления программы производится проверка ее достоверности на контрольном примере. На этом подэтапе необходимо оценить затраты машинного времени для расчета одной реализации моделируемого процесса, что позволит разработчику модели правильно сформулировать требования к точности и достоверности результатов моделирования. 4 Проведение машинных экспериментов с моделью системы На этом этапе проводятся серийные расчеты по составленной и отлаженной программе. Этап включает следующие подэтапы: планирование машинного эксперимента; проведение рабочих расчетов; представление результатов моделирования; интерпретацию результатов моделирования; выдачу рекомендаций по оптимизации режима работы реальной системы. Перед проведением рабочих расчетов на ЭВМ должен быть составлен план проведения эксперимента с указанием комбинаций переменных и параметров, для которых должно проводиться моделирование системы. Задача заключается в разработке оптимального плана эксперимента, реализация которого позволяет при сравнительно небольшом числе испытаний модели получить достоверные данные о закономерностях функционирования системы. Результаты моделирования могут быть представлены в виде таблиц, графиков, диаграмм, схем и т.п. В большинстве случаев наиболее простой формой считаются таблицы, хотя графики более наглядно иллюстрируют результаты моделирования системы. Интерпретация результатов моделирования имеет целью переход от информации, полученной в результате машинного эксперимента с моделью, к выводам, касающимся процесса функционирования объекта-оригинала. На основании анализа результатов моделирования принимается решение о том, при каких условиях система будет функционировать с наибольшей эффективностью. Типовые математические схемы. В процессе создания математической модели, реализуемой на ЭВМ, происходит переход от содержательного описания к формальному алгоритму. Промежуточным звеном между ними может служить математическая схема. Существует ряд типовых математических схем, которые могут лечь в основу разрабатываемого конкретного моделирующего алгоритма. К ним относятся следующие схемы (модели): непрерывно-детерминированные модели (D-схемы); дискретно-детерминированные модели (F-схемы); дискретно-стохастические модели (Р-схемы); непрерывно-стахастические модели (Q-схемы). К непрерывно-детерминированным моделям относятся модели, описываемые системами обыкновенных дифференциальных уравнений или уравнений в частных производных. В качестве независимой переменной, от которой зависят неизвестные искомые функции, обычно служит время. Тогда вектор-функция искомых переменных будет непрерывной. Математические схемы такого вида отражают динамику изучаемой системы и поэтому называются D – схемами.(англ.dynamic). К дискретно детерминированным моделям относятся так называемые конечные автоматы. Автомат можно представить как некоторое устройство, на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. У конечного автомата множество входных сигналов и внутренних состояний является конечным множеством. Название F-схема происходит от английских слов finite autotomata. К дискретно-стохастическим моделям относятся вероятностные (стохастические)автоматы или по-английски probabilistic automat . Отсюда название – Р-схема. В общем виде вероятностный автомат можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано стохастически. Примеры типовой схемы непрерывно-стохастического типа может служить схема системы массового обслуживания (СМО) или по английски queueing system. Отсюда название – Q-схема. В качестве процесса обслуживания в СМО могут быть представлены различные по физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки товаров, потоки продукции, потоки деталей, потоки клиентов и т.п. Для любой системы массового обслуживания характерно наличие трех отличительных свойств: объектов, у которых может возникнуть потребность в удовлетворении некоторых заявок: агрегатов, предназначенных для удовлетворения заявок на обслуживание; специальной организации приема в систему заявок и их обслуживания. Схема системы массового обслуживания показана на рисунок 9. 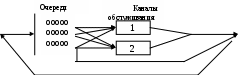 Входящий Выводящий поток поток Обратная связь Рисунок 9 - Схема системы массового обслуживания Совокупность заявок рассматривают как поток событий, т.е. последовательность событий, происходящих в случайные моменты времени. Время обслуживания заявки также считается случайной величиной. Из-за совместного действия этих двух случайных факторов количество обслуженных заявок в заданном интервале времени является случайной . Исследование моделей СМО ставит целью установление параметров случайных величин, характеризующих процесс обслуживания заявок. Существует несколько разновидностей СМО: по числу каналов обслуживания СМО делятся на одноканальные и многоканальные; по числу фаз (последовательно соединенных агрегатов) СМО делятся на однофазные и многофазные; по наличию обратной связи СМО делятся на разомкнутые (с бесконечным числом заявок) и замкнутые (с конечным числом заявок); по наличию очереди СМО делятся н системы без очередей (с потерями заявок), системы с неограниченным ожиданием (по времени иди длине очереди) и системы с ограниченным ожиданием (по времени или длине очереди); по принципу формирования очередей СМО делятся на системы с общей очередью и системы с несколькими очередями; по наличию отказов СМО делятся на системы с отказами м системы без отказов; по виду приоритета СМО делятся на системы со статическим приоритетом (обслуживание в порядке поступления заявок) и системы с динамическим приоритетом, который, в свою очередь, имеет три разновидностей: относительный приоритет (заявка высокого приоритета ожидает окончания обслуживания заявки с более низким приоритетом); абсолютный приоритет (заявка высокого приоритета при поступлении немедленного вытесняет заявку с более низким приоритетом); смешанный приоритет (заявка с низшим приоритетом обслуживалась в течение времени, меньше критического абсолютный приоритет, в противном случае используется относительный приоритет). Способы построения моделирующих алгоритмовСуществуют следующие способы (или принципы) построения моделирующих алгоритмов: способ повременного моделирования с постоянным шагом; способ повременного моделирования с переменным шагом; способ последовательной проводки заявок; способ поэтапной последовательности проводки заявок. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
