имитнов2008. Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности

• Название: Учебнометодический комплекс по дисциплине Имитационное моделирование для студентов Казнту имени К. И. Сатпаева по специальности
• Дата: 28.01.2022
• Размер: 1.61 Mb.
• Имя файла: имитнов2008.doc
• Тип: Учебно-методический комплекс; #344977
• страница: 8 из 10

Рисунок 21 - Схема алгоритма процедур обработки прерываний

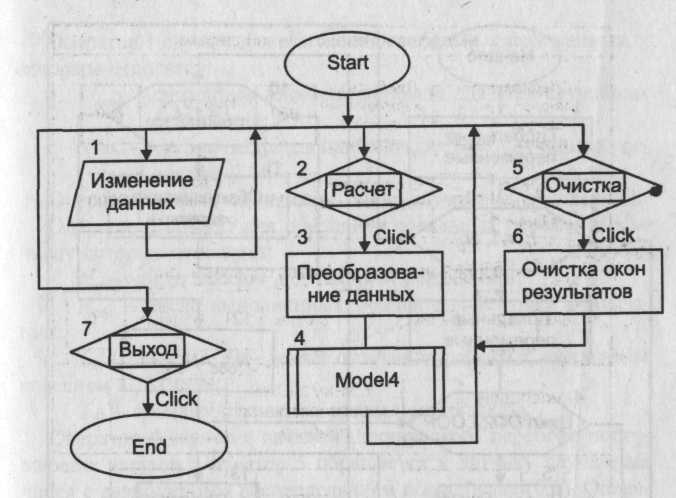
После нажатия на панели инструментов кнопки «Start» акти­визируется стартовая форма. С этого момента программа нахо­дится в режиме ожидания действий пользователя.

Цифрой 1 обозначено действие, заключающееся в корректи­ровке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.

Цифрой 2 обозначено действие, заключающееся в нажатии кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model4». Схема алгоритма этого модуля приведена на рисунке 22. После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Программа вновь переходит в режим ожидания действий пользователя.

Цифрой 5 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстовых полей для вывода по­казателя эффективности и значения числового фактора. Затем может быть произведено изменение исходных данных и прове­дены новые расчеты с использованием кнопки «Расчет».

Цифрой 7 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Выход». В результате работа про­граммы прекращается.

В состав базового комплекта исходных данных входят:

L_z - среднее число заказов в день;

T _обл._j (j =1, 2, 3, 4) - среднее время работы с изделием в j -м цехе для выбранного варианта структуры предприятия (дней);

Р - прибыль от изготовления одного изделия ($);

С - издержки производства за период функционирования фирмы (в $);

T_D - период функционирования фирмы (дней);

- относительная величина разброса времени работы в каждом цехе;

N_P - число случайных реализаций моделируемого про­цесса.

Оператор 1 служит для обнуления глобальных переменных, к которым относятся:

M_prof - суммарная величина прибыли для всех случайных реализаций;

Sum2- сумма квадратов прибыли для всех случайных ре­ализаций.

Оператор 2 является началом цикла случайных реализаций. Оператор 3 служит для обнуления локальных переменных, к числу которых относятся:

N_z - число заказов для текущей реализации;

N_обс. - число выполненных заказов для текущей реализа­ции;

Т_kj (j=1, 2, 3, 4) — время окончания работы с очередным изделием в j-м цехе;

Т_Z0 - время поступления предыдущего заказа.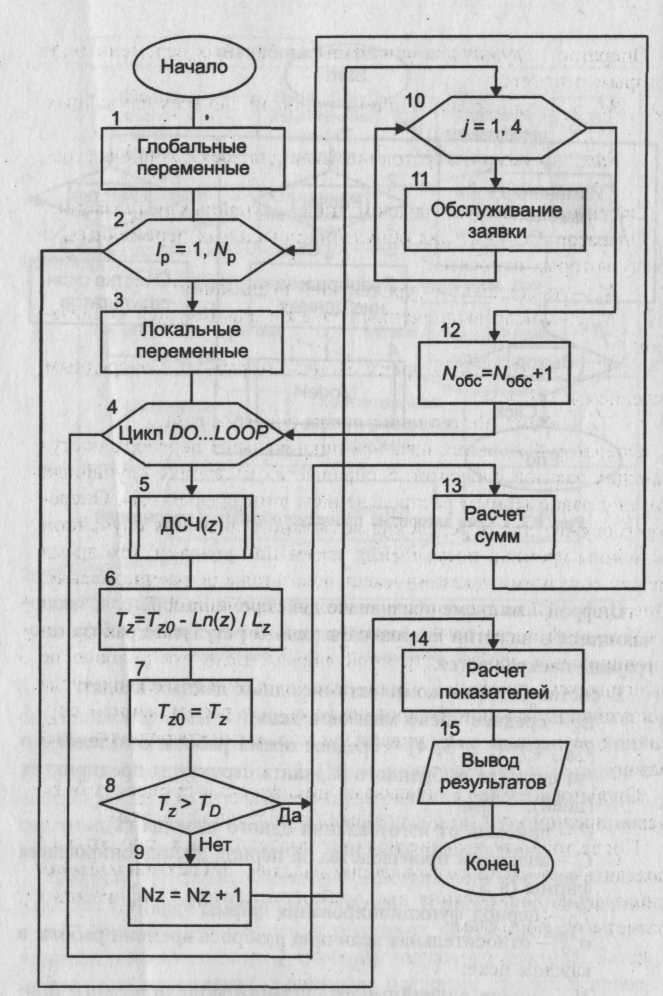






Рисунок 22 - Схема алгоритма модуля «Model 4»

Оператор 4 является началом циклического перебора посту­пающих заказов. Оператор 5 обращается к датчику случайных чисел с равномерным распределением в интервале (0,1). Опера­тор 6 служит для определения возможного значения случайной величины времени поступления заказа при условии, что время между соседними заказами имеет показательное распределение. Оператор 7 фиксирует новое значение переменной Т_Z0

Условный оператор 8 проверяет условие прекращения функ­ционирования производственной фирмы. Если это условие не выполняется, оператор 9 увеличивает на единицу счетчик числа поступивших заказов. В противном случае расчет данной слу­чайной реализации заканчивается и управление передается опе­ратору 13.

Операторы 10 и 11 описывают циклический процесс работы цехов предприятия по обслуживанию очередной заявки.

После того как изделие покинет последний цех, оператор 12 подсчитывает число изготовленных изделий. После окончания пе­риода функционирования предприятия оператор 13 производит расчеты по формулам:

Prof=N_обс*P-C;

M_prof =M _prof +Prof;

Sum2 = Sum2 + Prof  Prof

После окончания цикла случайных реализаций оператор 14 производит расчеты показателя эффективности по формулам: C_prof=M_prof / N_P;

C_prof = C_prof –1.28
Основная литература: 1[55-111]

Контрольные вопросы:

1.Как определяется случайная прибыль?

2. 
   Чему равно количество цехов?
   

Тема лекции № 7. Моделирование процессов и систем управления.

Модель управления запасами.

Имеется склад, где хранится запас однотипного товара. Начальный уровень запаса равен N_yp. В результате удовлетворе­ния ежедневного спроса происходит уменьшение запаса на случайную величину, имеющую нормальное распределение с из­вестными характеристиками: математическим ожиданием М_д и средним квадратическим отклонением _д. Затраты на хранение единицы товара в течение суток составляют $С₁,.

Если на складе не останется товара, то администрации склада придется уплатить прибывшим покупателям компенсацию в раз­мере $С₃ за каждую недостающую единицу товара по отноше­нию к заказанному количеству.

Чтобы избежать затрат, вызванных дефицитом товара, админи­страция склада периодически подает заявки на поставку допол­нительных партий товара выбранного объема Part. Подача заявки производится в момент, когда уровень запаса товара снизится до выбранного уровня UR_min. Время выполнения заявки является случайной величиной с нормальным распределением и известны­ми характеристиками М_т и _т. Затраты на поставку единицы това­ра составляют $С₂. Цикл работы склада составляет T_D дней.

Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы скла­да, обеспечивающий минимальные затраты на его содержание.

В частности, требуется установить:

- оптимальный уровень запаса UR_min, при достижении которого необходимо подавать заявку на поставку партии товара;

- оптимальный объем партии товара Part.

В качестве показателя эффективности моделируемого про­цесса целесообразно выбрать максимальные гарантированные затраты на содержание склада (с заданным уровнем гарантии), определяемые по формуле

C_gar = М_с +R - _с,

где М_с - средние затраты на содержание склада в течение периода T_D дней;

_с - среднее квадратическое отклонение затрат на содержание склада;

К_а - квантиль, зависящий от уровня гарантии а (K_а=1,28 при а=0,9).

В качестве критерия выбора оптимального режима рабо­ты склада может быть принят минимум максимальных гаран­тированных затрат:

К(UR _min., Part^*) ; MIN { C_gar (UR_min Part) },

где UR_min - оптимальное значение уровня запаса товара, при достижении , которого необходимо подавать заявку на поставку новой партии;

Part^*- оптимальный объем партии товара.

Схема алгоритма процедур обработки прерываний, связанных с объектами стартовой формы, показана на рисунке 23.

После нажатия кнопки «Start» активизируется стартовая фор­ма. С этого момента программа находится в режиме ожидания действий пользователя.

Цифрой 1 обозначено действие, заключающееся в корректи­ровке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.

Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model3». Схема алгоритма этого модуля приведена на рисунке 25.

После окончания работы модуля и выдачи на экран результа­тов моделирования работа процедуры, связанной с кнопкой «Рас­чет», заканчивается. Программа вновь переходит в режим ожи­дания действий пользователя.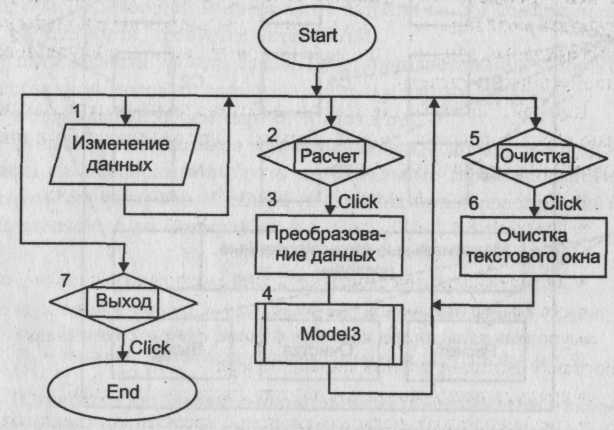

Рисунок 24- Схема алгоритма процедур обработки прерываний

Цифрой 5 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстового поля для вывода ре­зультата моделирования. Затем может быть произведено измене­ние исходных данных и проведены новые расчеты с использова­нием кнопки «Расчет».

Цифрой 7 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Выход». В результате работа про­граммы прекращается.

В состав базового комплекта исходных данных входят:

• 
  начальный уровень запаса товара - N_ур;
  
• 
  средний ежедневный спрос товара - M_д;
  
• 
  среднее квадратическое отклонение ежедневного спроса - _д;
  
• 
  объем партии товара - Part;
  
• 
  уровень запаса, при котором должна оформляться заявка на
  поставку дополнительной партии товара, - UR_min;
  
• 
  среднее время поставки партии товара - М_т дней;
  
• 
  среднее квадратическое отклонение времени поставки това­ра - _T дней;
  
• 
  стоимость хранения единицы товара в течение суток - $С₁;
  
• 
  стоимость поставки единицы товара - $С₂;
  
• 
  стоимость затрат на компенсацию отсутствия товара на скла­де - $С₃ за каждую недостающую единицу;
  
• 
  период функционирования склада - T_D дней;
  
• 
  число случайных реализаций - N_p.
  

Блок 1 обеспечивает обнуление глобальных переменных, к которым относятся:

MS_C - начальное значение суммы случайных величин об­щих затрат на содержание склада для различных ре­ализаций моделируемого процесса; SS_C - начальное значение суммы квадратов случайных ве­личин общих затрат.

Кроме того, в этом же блоке устанавливается начальное зна­чение времени поставки дополнительной партии товара, кото­рое выходит за пределы периода работы склада и равняется

Т_пост.0= Т_D+ 1.

Оператор 2 представляет собой заголовок цикла случайных реализаций.

Блок 3 производит обнуление локальных переменных, к кото­рым относятся:

S_C1 - начальное значение суммарных затрат на хранение то­вара в течение всего периода работы склада для од­ной реализации;

S_C2 - начальное значение суммарных затрат, связанных с нехваткой товара в течение всего периода работы склада для одной реализации;

S_C3 - начальное значение суммарных затрат на поставку до­полнительных партий товара в течение всего перио­да работы склада для одной реализации;

Т - исходное значение счетчика дней (модельное время);

Zajav - числовой признак отсутствия заявки на поставку дополнительной партии товара (если заявка подана, то Zajav =1).

В этом же блоке планируемое время поставки партии товара приравнивается к его начальному значению, т. е. T_пост = T_пост.0. Наконец, текущий уровень запаса товара приравнивается к его начальному уровню: V=N_yp.

Оператор 4 является началом циклического перебора дней работы склада. Оператор 5 увеличивает модельное время на один шаг (на одни сутки). Условный оператор 6 проверяет условие продолжения работы склада для каждой случайной реализации.

Оператор 7 обращается к процедуре «Norm», формирующей возможное значение нормированной, центрированной случайной величины с нормальным распределением. Оператор 8 определя­ет возможное значение величины случайного ежедневного спро­са при заданном его математическом ожидании М_д и среднем квадратическом отклонении 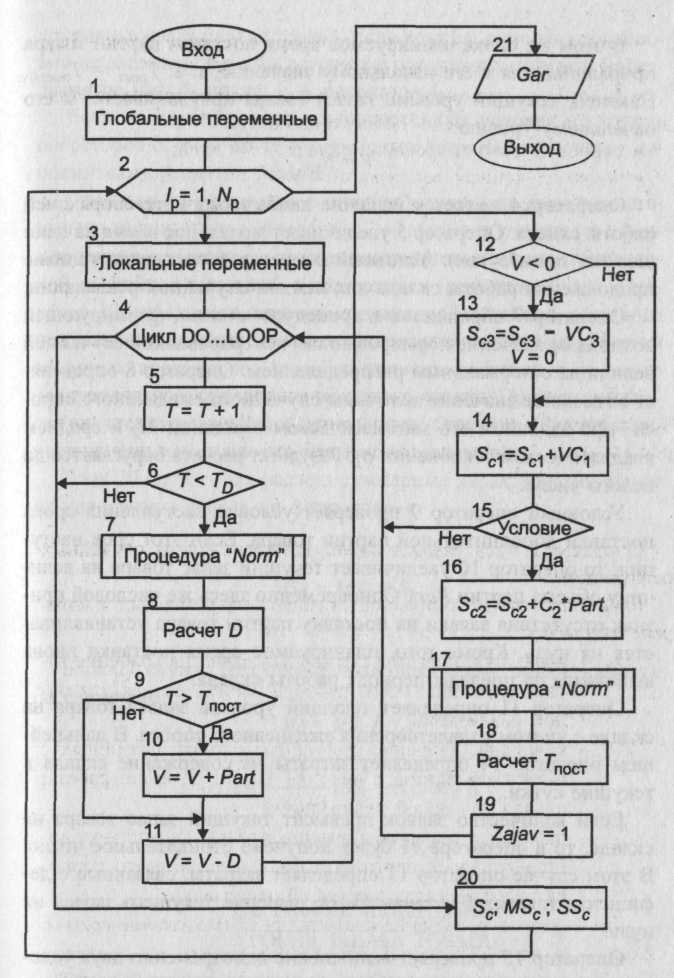_д. Результат расчета округляется до целого числа.



Рисунок 25 - Схема алгоритма модуля «ModeI3»

Условный оператор 9 проверяет условие наступления срока поставки дополнительной партии товара. Если этот срок насту­пил, то оператор 10 увеличивает текущий запас товара на вели­чину объема партии Part. Одновременно здесь же числовой при­знак отсутствия заявки на поставку партии товара устанавлива­ется на нуль. Кроме того, планируемое время поставки вновь выводится за пределы периода работы склада.

Оператор 11 определяет текущий уровень запаса товара на складе с учетом удовлетворения ежедневного спроса. В дальней­шем оператор 14 определяет затраты на содержание склада в текущие сутки.

Если количество заявок превысит текущий запас товара на складе, то в операторе 11 будет получено отрицательное число. В этом случае оператор 13 определяет затраты, связанные с де­фицитом товара, и устанавливает значение текущего запаса на нуль.

Оператор 15 проверяет выполнение одновременно двух усло­вий: превышает ли текущий запас минимально допустимый (кри­тический) уровень и была ли уже оформлена заявка на поставку дополнительной партии товара. Если хотя бы одно из этих усло­вий не выполняется, то в алгоритме происходит передача управ­ления на начало цикла, т. е. оператору 4.

Если же одновременно выполняются оба условия, то группа операторов с 16-го по 19-й определяет затраты на поставку до­полнительной партии товара.

Оператор 16 увеличивает текущие затраты на величину сто­имости партии товара. Оператор 17 обращается к процедуре фор­мирования возможного значения нормированной, центрирован­ной случайной величины с нормальным распределением. Опе­ратор 18 определяет возможное значение случайной величины времени выполнения заявки на поставку партии товара с учетом заданных параметров: среднего времени поставки и среднего квадратического отклонения времени поставки. При этом резуль­тат расчета округляется до целого числа. Оператор 19 устанавли­вает на единицу числовой признак подачи заявки.

Блок 20 служит для расчета суммарных характеристик затрат на содержание склада по формулам:

S_C=S_C1+S_C2+S_C3;

MS_C=MS_C+S_C;

SS_C=SS_C+Sc+S_C.

Блок 21 служит для определения показателя эффективности по формулам:

М_с = MS_C/N_p;

= ;

Gar = M_c+ 1,28 * .

График изменения уровня запаса товара.

Типовой график изменения уровня запаса товара на складе с учетом дополнительных поставок показан на рисунке 26.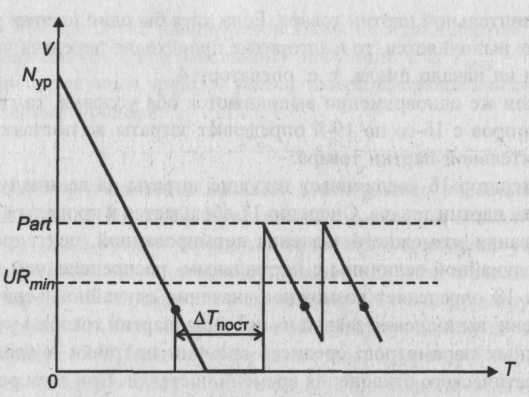

Рисунок 26 - График изменения запаса товара на складе

В начальный момент на складе имеется N_yp единиц товара. В этот момент числовой признак подачи заявки на поставку допол­нительного товара Zajav=0, а время поставки превышает время окончания работы склада.

В результате удовлетворения случайного ежедневного спроса уровень запаса товара снижается. Если уровень запаса товара снизится ниже величины UR_min, то подается заявка на поставку дополнительной партии товара объемом Part единиц. В этот момент числовой признак Zajav становится равным единице, а время выполнения поставки определяется по формуле

T_пост= Т+ _пост= Т+Мт+n- _т,

где Т - текущее модельное время (в днях);

_пост - период выполнения заказа;

М_т - среднее время выполнения заказа;

_т — среднее квадратическое отклонение времени выполнения заказа;

n - возможное значение нормированной, центрированной случайной величины с нормальным распределением.

Когда модельное время становится равным T_пост, поступает партия товара, и текущий уровень запаса товара скачком увеличивается на величину Part. В этот момент числовой признак Zajav становится равным нулю, а время поступления партии товара вновь приравнивается величине Т_посг/0.

Модель торговой точки

Имеется подвижная торговая точка, которая производит тор­говлю в трех различных пунктах. Торговая точка реализует три вида товаров. Выручка, полученная от продажи каждого вида товара, является случайной величиной с усеченным нормальным распределением. Предполагается также, что на каждом пункте с некоторой заданной вероятностью торговой точке будет причи­нен внеплановый убыток. Размер этого убытка можно считать случай­ной величиной, имеющей усеченное нормальное распределение с заданными параметрами.

Для каждого пункта торговли задан комплект входных пара­метров:

1. 
   Т_ср._ij- среднее значение дневной выручки от продажи j-ro
   товара на i-м пункте (i= 1, 2, 3 и j= 1, 2, 3);
   
2. 
   P_i- вероятность того, что на данном пункте торговой точке
   будет причинен внеплановый убыток;
   

3) U_i-средняя величина внепланового убытка.

Кроме того, в число входных параметров входят:

4) - относительная величина среднего квадратического отклонения дневной выручки, одинаковая для всех пунктов торговли и всех видов товара и используемая для определения возможного значения случайной выручки Т_ijпо формуле

Т_ij = T_cp._ij(l + ), (i=1,2,3; j=1, 2, 3),

где -возможное значение случайной величины с усеченным нормальным распределением;

5) -относительная величина среднего квадратического отклонения внепланового убытка, одинаковая для всех пунктов торговли и используемая для определения возможного значения случайного убытка U_i, по формуле

U_i = U_ср.i (1 + ), (i=1, 2, 3; j=1, 2, 3);

6) T_min - заданное минимальное значение случайной величины для эталонного усеченного нормального распределения (используемое при генерировании величины );

7) T_vах - заданное максимальное значение случайной величи­ны для эталонного усеченного нормального распределения (ис­пользуемое при генерировании величины ).

Величины T_min и T_vах используются в процедуре, вырабаты­вающей возможные значения случайной величины, имеющей усеченное нормальное распределение.

Примем дополнительное допущение:

= = .

Суммарная выручка от продажи всех видов товара с учетом убытка составляет случайную прибыль. В качестве показателя эффективности работы i-й торговой точки примем минимальную гарантированную прибыль, определяемую по следующей зави­симости:

Gar_пр.i = М_пр.i - К_а 

где М_пр.i - математическое ожидание (среднее значение) прибыли для i –го пункта торговли;

= среднее квадратическое отклонение прибыли для i -го пункта торговли;

К_а - квантиль нормального распределения, соответствующий заданной надежности а (АГ_а=1,28 при а=0,9).

Задача исследования может заключаться в определении усло­вий, при которых все пункты торговли будут равноценными по величине приносимой прибыли. В этих условиях необходимо установить, какова функциональная связь между увеличением среднего убытка и компенсирующим его уменьшением вероят­ности причинения убытка.

Схема алгоритма процедур обработки прерываний показана на рисунке 27.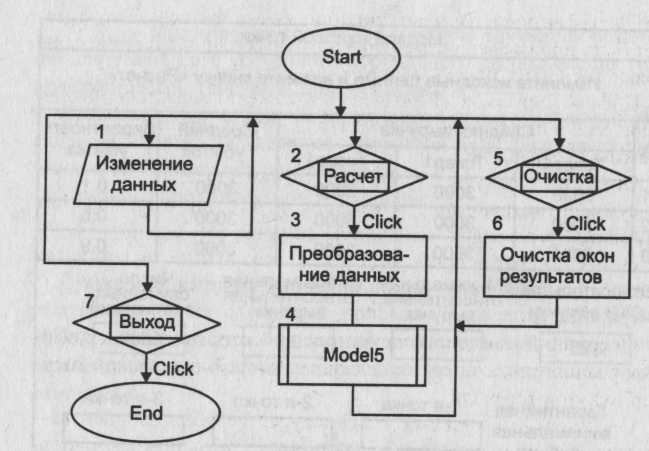



Рисунок 27- Схема алгоритма процедур обработки прерываний

После нажатия кнопки «Start» активизируется стартовая фор­ма. С этого момента программа находится в режиме ожидания действий пользователя.

Цифрой 1 обозначено действие, заключающееся в корректи­ровке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.

Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model 5». Схема алгоритма этого модуля приведена на рисунке 28. После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Программа вновь переходит в режим ожидания действий пользователя.

Цифрой 5 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстовых полей для вывода показателя эффективности и значения числового фактора. Затем мо­жет быть произведено изменение исходных данных и проведены новые расчеты с использованием кнопки «Расчет».

Цифрой 7 на схеме обозначено действие пользователя, заклю­чающееся в нажатии кнопки «Выход». В результате работа про­граммы прекращается.

Оператор 1 обнуляет глобальные переменные:

-суммарную прибыль для каждого пункта торговли для всех случайных реализаций моделируемого процесса T_sumi (i=l, 2, 3);

-сумму квадратов прибыли для каждого пункта торговли для всех случайных реализаций моделируемого процесса T_SUm2._i (i=1, 2, 3).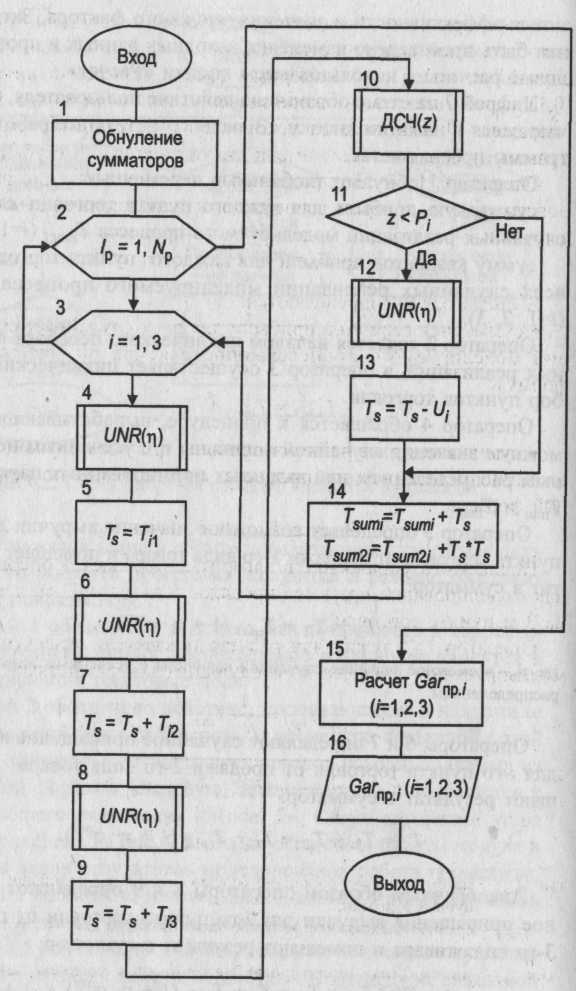




.

Рисунок 28 - Схема алгоритма модуля «Model J»

Оператор 2 является началом циклического перебора случай­ных реализаций, а оператор 3 осуществляет циклический пере­бор пунктов торговли.

Оператор 4 обращается к процедуре, вырабатывающей воз­можные значения случайной величины  с усеченным нормаль­ным распределением при заданных нормированных параметрах T_min и T_max

Оператор 5 определяет возможное значение выручки для 1-го пункта торговли от продажи 1-го вида товара и помещает резуль­тат в сумматор:

T_s =T_i1 = T_ср,_i1(1+ ,)

где - возможное значение случайной величины с усеченным нормальным распределением.

Операторы 6 и 7 определяют случайное приращение выручки для i-го пункта торговли от продажи 2-го вида товара и поме­щают результат в сумматор:

Ts = T_s + T_i2 = T_s + T_cp._i2 (1 + )

Аналогичным образом операторы 8 и 9 определяют случай­ное приращение выручки для i-го пункта торговли от продажи 3-го вида товара и помещают результат в сумматор:

T_S=T_S +T_i3 = T_s+T_cp.i3(1+ ).

Операторы 10 и 11 моделируют появление случайного собы­тия с заданной вероятностью. Оператор 10 с помощью датчика случайных чисел с равномерным распределением в интервале (0,1) вырабатывает возможное значение этой величины z. Если в операторе 11 выполняется условие z < P_i то считается, что в данном пункте торговли имели место внеплановые убытки.

Операторы 12 и 13 определяют возможное значение внепла­нового убытка, который вычитается из накопленной суммарной выручки:

T_s =T_s-U_i = Т_s-U_срi (1+ ).

В операторе 14 определяются:

• суммарная величина прибыли для всех случайных реализа­ций моделируемого процесса, определяемая по рекурсивной формуле : T_sum.i ⁼ T_{sum i} + T_s

• сумма квадратов величин прибыли для всех случайных реализаций моделируемого процесса, определяемая по рекурсивной формуле: T_sum2.i ⁼ T_{sum2 i} + T_sT_s

После этого управление в алгоритме передается оператору 3 для моделирования процесса продажи товаров на 2-м, а затем и на 3-м пункте торговли.

Оператор 15 служит для расчета показателя эффективности моделируемого процесса по следующим зависимостям:

M_np.i = * T_sum.i;



Gar_пp,i = M_np.i - К_а-

где M_np.i - математическое ожидание (среднее значение) прибыли для 1-го пункта торговли;

-среднее квадратическое отклонение прибыли для i-го пункта торговли;

Gar_пp,i - минимальная гарантированная прибыль с уровнем гарантии а (при а=0,95 квантиль нормального распределения К_а= 1,645).

Оператор 16 выводит на экран значения показателей эффек­тивности для всех трех пунктов торговли.
Основная литература:1 [ 83-123]

Контрольные вопросы

1. 
   Чему равны затраты на содержание склада?
   
2. 
   Перечислить характеристики затрат.
   
3. 
   Чему равна гарантированная прибыль?
   
4. 
   Чему равно математическое ожидание?
   

2.3 Планы практических занятий

Практическое занятие №1. Моделирование базовой последовательности

Задание 1. Метод усечения: Разряды очередного случайного числа получают путем отбрасывания или «усечения» части разрядов у результата нелинейного преобразования над одним или несколькими предыдущими числами.

Методические рекомендации: Практическая реализация этого метода осуществляется с помощью алгоритма «середины квадратов» (алгоритм Дж.Неймана) и модифицированного алгоритма Дж.Неймана. В этих алгоритмах случайные числа предполагаются 2К-значными



Алгоритм «середины квадратов».

Шаг 1. Возвести в квадрат z_n:



Шаг 2. Отобрать средние 2К цифр квадрата и считать следующей реализацией последовательности число



Пример.

z₀ = 0.3124; ; z₁ = 0.7593; ;

z₂ = 0.6536; ; z₃ = 0.7192; ;

z₄= 0.7248 и т. д.

Модифицированный алгоритм Неймана отличается от алгоритма «середины квадратов» тем, что вместо операции возведения в квадрат используется операция умножения двух предыдущих чисел последовательности.

Задание 2. Метод вычетов. Метод основан на реализации линейной формулы

, (1.3)

где Z_n^*, a, c, M – неотрицательные целые числа, Z^*_n+1 – наименьший положительный вычет а Z_n^* + c по модулю М, а – множитель, с – приращение. По формуле (1.3) получают псевдослучайные числа, равномерно распределенные в интервале [0,М]. Чтобы получить числа, равномерные в интервале [0,1], необходимо выполнить дополнительное преобразование:

(1.4)

Методические рекомендации: Рассмотрим численный пример.

Пусть а = с = Z₀^* = 7, М = 10.

Z₁^* = 7*7+7(mod10) = 6; Z₁ =0.6;

Z₂^* = 7*6+7(mod10) = 9; Z₂ =0.9;

Z₃^* = 7*9+7(mod10) = 0; Z₃ =0;

Z₄^* = 7*0+7(mod10) = 7; Z₄ =0.7 и т. д.

Алгоритм формирования базовой последовательности по методу вычетов состоит из следующих шагов:

- ввод начальных значений;

• 
  расчет очередного значения случайного числа по (1.3) и (1.4).
  

С помощью алгоритма «середины квадратов» и метода вычетов получить случайные числа. Составить блок-схему алгоритма «середины квадратов».
Основная литература: 5.9

Контрольные вопросы:

1. Просчитать численные примеры для начальных значений методом усечения: Z₀ = 0.1542 и Z₀ = 0.4500. Сравнить полученные результаты.

2.Просчитать численный пример для следующих начальных значений: а = с=6, М = 18, Z₀^* = 2 методом вычетом

3. Просчитать численный пример для следующих начальных значений: а=с=4 Z₀^* = 4, М=10 методом вычетов. Составить блок-схему алгоритма метода вычетов.

4.Просчитать численный пример для следующих начальных значений:

Z₀ = 3,14159, Z₁ = 0.542102, n=10 алгоритмом Дэвиса.
Практическое занятие № 2. Моделирование базовой последовательности

Задание 1. Метод суммирования. Основная формула метода имеет вид :

.

Частным случаем этого метода являются аддитивные алгоритмы, использующие формулу:

где k  16.

При соответствующем выборе начальных значений Z₀, Z₁, …, Z_k эта формула является хорошим источником случайных чисел.

Следует также отметить алгоритм Дэвиса, который принял к=1 и, удачно выбрав первые два начальные числа (Z₀= , Z₁= 5¹⁷*2^-42 = 0,542101887), получил хорошую последовательность равномерных чисел. Алгоритм Дэвиса использует формулу



Методические рекомендации: Практическую реализацию алгоритма Дэвиса удобно осуществить по следующим шагам:

Шаг 1. Вычислить Т = Z₀+Z₁ и принять Z₀=Z_1.