Корпоративные финансы ( лекции). Учебное пособие Направление подготовки магистры Уфа 2017 Содержание Введение стр
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Доходность облигации без права досрочного погашения Оценка стоимости подобной облигации выполняется по формуле (3.7). Предполагается, что в этой формуле известны все показатели, кроме r (в левой части формулы в этом случае берется текущая рыночная цена актива). Разрешая уравнение относительно r, определяем общую доходность данной облигации. Этот показатель в отечественной финансовой прессе иногда называется доходностью к погашению и обозначается YTM (Yield to Maturity). Отметим, что в условиях эффективного рынка все облигации одного класса теоретически должны иметь примерно одинаковую доходность. Доходность купонной облигации без права досрочного погашения рассчитывается отношением среднегодового дохода (годовой процент плюс часть разницы между нарицательной стоимостью и ценой покупки облигации) к средней величине инвестиции и дает приблизительную оценку показателя r: YTM = 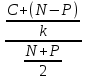 , (3.17.) , (3.17.)где N - номинал облигации, P - текущая цена (не имеет оценки), C - купонный доход, k - число лет, оставшихся до погашения облигации. Достоинством показателя YTM, как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе при выборе вариантов инвестирования в те или иные облигации. Иногда для оценки эффективности инвестирования в облигации рекомендуют ориентироваться на показатель текущей, или дивидендной, доходности (kd), под которым понимается отношение дохода, получаемого ежегодно по купонной ставке, к фактическим затратам на приобретение облигации: kd = 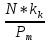 , (3.18.) , (3.18.)где N - номинальная стоимость облигации, Pm - текущая рыночная цена облигации, kk- купонная ставка, %. Из формулы (3.18.) видно, что показатель текущей доходности не может использоваться в качестве обобщенной характеристики и критерия при анализе целесообразности инвестирования в данные облигации. Он дает искаженную оценку реальной (т.е. общей) доходности облигации, поскольку в этом случае не учтен доход ее держателя, полученный от приобретения облигации с дисконтом. Поэтому более правильным является ориентация на показатель YTM. Еще одной характеристикой доходности облигации является показатель купонной доходности, рассчитываемый по следующей формуле: kk = 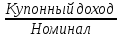 *100%, (3.19.) *100%, (3.19.)Чаще всего этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходности облигации невысока, а именно эта ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она используется в основном для расчета купонного дохода. Доходность облигации с правом досрочного погашения Облигации с правом досрочного погашения в отличие от рассмотренных выше имеют еще одну характеристику – доходность досрочного погашения (Yield to Call, YTC). Этот показатель дает оценку доходности на момент отзыва облигации с рынка, или ее досрочного погашения. Показатель YTC находится из формулы (3.7), в которой номинал N заменен выкупной ценой Pc. Доходность конвертируемой облигации Конвертируемая облигация предусматривает при выполнении некоторых условий возможность ее обмена на n-е число обыкновенных акций эмитента. Обмен может осуществляться, например, на основании коэффициента конверсии rc. В этом случае облигация имеет так называемую конверсионную стоимость (Pc), которая связана с рыночной ценой базисного актива (обыкновенной акции) Ps следующим соотношением: Pc= Ps* rc, (3.20.) Таким образом, для оценки ожидаемой доходности конвертируемой облигации можно воспользоваться алгоритмами, используемыми в случае с облигациями с правом досрочного погашения, в которых выкупная цена заменена ожидаемой конверсионной стоимостью. Основным моментом в процессе анализа является установление прогнозной оценки стоимости базисного актива на тот или иной момент времени. Доходность акции Доходность бессрочной привилегированной акции, равно как и обыкновенной акции, с неизменным дивидендом, находится по формуле: kt = 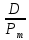 , (3.21.) , (3.21.)где D - ожидаемый дивиденд, Pm - текущая рыночная цена акции. Следует отметить, что при принятии решения о целесообразности покупки акции на основе формулы (3.18.) неявно имеется в виду, что после покупки акции инвестор не предполагает продать ее в ближайшем будущем. Поэтому общая доходность здесь совпадает с текущей дивидендной доходностью. Считается, что такой оценки в принципе достаточно для принятия решения; в дальнейшем при возникновении необходимости по некоторым причинам продать акцию могут быть рассчитаны фактические значения других показателей доходности. Если инвестор приобретает акцию в спекулятивных целях, намереваясь продать ее через некоторое время, то он может получить некоторые оценки ожидаемых значений общей, дивидендной и капитализированной доходности. В данном случае можно воспользоваться формулой: kt = kd + kc = 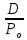 = =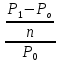 , (3.22.) , (3.22.)где Po - рыночная цена акции на момент принятия решения о покупке; P1 - ожидаемая цена акции на момент предполагаемой ее продажи; n - ожидаемое число лет владения акцией. Оценка ожидаемой доходности конвертируемой привилегированной акции также может быть получена с помощью формулы (3.19.), в которой в качестве P1 следует использовать ожидаемую конверсионную стоимость акции. Для оценки значений ожидаемой общей доходности обыкновенных акций с равномерно возрастающими дивидендами можно воспользоваться формулой, полученной на основании модели Гордона (3.10): kt = kd + kс= 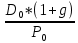 + g = + g = 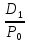 + g, (3.23.) + g, (3.23.)где D0 - последний полученный к моменту оценки дивиденд по акции; D1 - ожидаемый дивиденд; P0 - цена акции на момент оценки; g - темп прироста дивиденда. Из формулы (3.19.) видно, что ожидаемая капитализированная доходность обыкновенной акции с равномерно возрастающим дивидендом совпадает с темпом прироста дивиденда или с темпом прироста цены акции. Таким образом, показатель g имеет несколько интерпретаций: капитализированная доходность; темп прироста дивиденда; темп прироста цены акции. 3.6. Оценка эффективности фондового портфеля В сложившейся мировой практике фондового рынка под инвестиционным портфелем понимается некая совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, выступающая как целостный объект управления Смысл портфеля - улучшить условия инвестирования, придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятых ценных бумаг и возможные только при их комбинации. Теоретически портфель может состоять из ценных бумаг одного вида, а также менять свою структуру путем замещения одних ценных бумаг на другие. В процессе формирования портфеля достигается новое инвестиционное качестве с заданными характеристиками. Портфель ценных бумаг является финансовым инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске Доходы по портфельным инвестициям представляют собой валовую прибыль по всей совокупности бумаг, включенных в тот или иной портфель с учетом риска. Возникает проблема количественного соответствия между прибылью и риском, которая должна решаться оперативно в целях постоянного совершенствования структуры уже сформированных портфелей и формирования новых, в соответствии с пожеланиями инвесторов. Надо сказать, что указанная проблема относится к числу тех, для выяснения которых достаточно быстро удается найти общую схему решения, но которые практически не разрешимы до конца. С учетом инвестиционных качеств ценных бумаг можно сформировать различные портфели ценных бумаг, в каждом из которых будет собственный баланс между существующим риском, приемлемым для владельца портфеля, и ожидаемой им отдачей (дохода) в определенный период времени. Формируя инвестиционный портфель, инвестор должен располагать методикой для оценки инвестиционных качеств ценных бумаг. Они оцениваются посредством методов фундаментального и технического анализа. Фундаментальный анализ оправдывает себя при длительной работе с крупными компаниями и при ориентации на среднесрочные и долгосрочные инвестиции, Приемы технического анализа более оперативны и основаны на информации о динамке биржевых курсов акций, что вполне достаточно для принятия инвестиционных решений. Часто данные методы используются в комбинации. Основной задачей такой оценки является выявление среди множества ценных бумаг той их части, в которую можно вложить денежные средства, не подвергая свои вложения высокому риску. На практике существует прямая зависимость между доходностью и уровнем риска ценных бумаг. По степени риска минимальный уровень имеют вложения в денежные средства, но они наименее доходны и подвержены обесцениванию в результате инфляции. Вторыми по степени риска являются облигации Банка России и муниципальные краткосрочные облигации (например, МКО Правительства Санкт-Петербурга). Третьими по степени риска являются вложения в банковские и корпоративные облигации, а за ними следуют акции известных промышленных компаний. Акционерные промышленные компании и финансовые посредники получают следующие доходы по ценным бумагам: проценты и дивиденды по ценным бумагам; доход от увеличения курсовой стоимости ценных бумаг, находящихся в портфеле (реализуется при их перепродаже в виде разницы между ценой покупки и ценой продажи); премии и разницы при вложении денежных средств в производные фондовые инструменты (опционы и фьючерсы); комиссионное вознаграждение, возникающее при управлении портфельными инвестициями и др. Доход инвестора от владения фондовыми инструментами равен доходу от роста их курсовой стоимости и текущего дохода. Для характеристики эффективности инвестиций в финансовые активы используют величину, равную отношению полного дохода к начальному объему инвестиций (в годовом интервале): Доходность инвестиций = 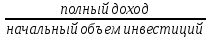 ×100, (3.24.) ×100, (3.24.)Полный доход инвестора от финансовых активов складывается из дохода от изменения цены актива (прироста капитала) и текущего дохода. Полный доход = текущий доход + прирост капитала, (3.25.) Прирост капитала может быть и отрицательной величиной, если стоимость актива снижается. Инвестор стремится вложить свои денежные средства в наиболее доходные финансовые активы. Однако неопределенность будущих доходов требует учета возможных отклонений доходности от ожидаемого значения, т.е. учета риска, связанного с вложениями в данный финансовый инструмент. Фондовый портфель имеет ограничения по сроку жизни, а также по минимальной и максимальной суммам инвестиций. Его доходность определяется трем величинами: ожидаемой, возможной и средней. Ожидаемая (минимальная) доходность – величина, которая будет получена по окончании срока жизни портфеля при сочетании наименее благоприятных обстоятельств. Возможная (максимальная) доходность– величина, получаемая при наиболее вероятном развитии событий. Более высокая доходность связана с повышенным риском для инвестора. Поэтому в процессе инвестирования следует учитывать оба фактора, которые сравниваются со среднерыночным уровнем доходности. Базовая формула совокупной доходности портфеля при использовании годового периода имеет вид: Доходность портфеля = 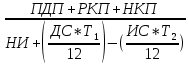 , (3.26.) , (3.26.)где ПДП - полученные дивиденды и проценты; РКП - реализованная курсовая прибыль; НКП - нереализованная курсовая прибыль; НИ - начальные инвестиции; ДС - дополнительные средства; Т1 - число месяцев нахождения денежных средств, вложенных в фондовые инструменты, в портфеле; ИС - извлеченные средства; Т2 – число месяцев отсутствия денежных средств, вложенных в фондовые инструменты, в портфеле. Данный способ сравнительного исследования очень удобен для инвестора, поскольку он может показать, насколько положительно зарекомендовал себя фондовый портфель относительно рынка ценных бумаг в целом. 3.7. Современные теории определения доходности и риска портфельных инвестиций Арсенал методов формирования портфеля достаточно обширен; наибольшим авторитетом в настоящее время пользуется теория инвестиционного портфеля Уильяма Шарпа (W.Sharpe) и Гарри Марковича (H.Markowitz). Основные принципы, изложенные в этой теории, следующие. Во-первых, успех инвестиций в основном зависит от правильного распределения средств по типам активов. Проведенные западными специалистами эксперименты показали, что прибыль определяется: на 94% выбором типа используемых инвестиционных инструментов (акции крупных компаний, краткосрочные казначейские векселя, долгосрочные облигации и др.); на 4% выбором конкретных ценных бумаг заданного типа; на 2% оценкой момента закупки ценных бумаг. Данный феномен объясняется тем, что бумаги одного типа сильно коррелируют, т.е. если какая-то отрасль испытывает спад, то убыток инвестора не очень зависит от того, преобладают в его портфеле бумаги той или иной компании. Во-вторых, риск инвестиций в определенный тип ценных бумаг определяется вероятностью отклонения прибыли от ожидаемого значения. Прогнозируемое значение прибыли можно определить на основе обработки статистических данных о динамике прибыли от инвестиций в эти бумаги в прошлом, а риск – как среднеквадратическое отклонение от ожидаемой прибыли. В-третьих, общая доходность и риск инвестиционного портфеля могут меняться путем варьирования его структурой. Существуют различные программы, позволяющие конструировать желаемую пропорцию активов различных типов, например минимизирующую риск при заданном уровне ожидаемой прибыли или максимизирующую прибыль при заданном уровне риска и др. В-четвертых, все оценки, используемые при составлении инвестиционного портфеля, носят вероятностный характер. Конструирование портфеля в соответствии с требованиями классической теории возможно лишь при наличии ряда факторов: сформировавшегося рынка ценных бумаг, определенного периода его функционирования, статистики рынка и др. Формирование инвестиционного портфеля осуществляется в несколько этапов: формулирование целей его создания и определение их приоритетности в частности, что важнее - регулярное получение дивидендов или рост стоимости активов, задание уровней риска, минимальной прибыли, отклонения от ожидаемой прибыли и т.п; выбор финансовой компании (это может быть отечественная зарубежная фирма; при принятии решения можно использовать ряд критериев: репутацию фирмы, ее доступность, виды предлагаемых фирмой портфелей, их доходность, виды используемых инвестиционных инструментов и т.п.); выбор банка, который будет вести инвестиционный счет. В условиях развитого рынка ценных бумаг формирование портфеля и управление им представляет достаточно сложный процесс; не случайно услуги специалистов по управлению портфельными инвестициями оцениваются весьма высоко. Крупные компании обычно имеют отдельное подразделение по портфельным инвестициям, в рамках которого формируется несколько портфелей в зависимости от состава включенных в них активов. Одним из важнейших понятий в теории портфельных инвестиций является понятие «эффективный портфель», под которым понимается портфель, обеспечивающий максимальную ожидаемую доходность при некотором заданном уровне риска или минимальный риск при заданном уровне доходности. Алгоритм определения множества эффективных портфелей был разработан Г. Марковицем в 50-е годы как составная часть теории портфеля. Сделанные им разработки были настолько фундаментальными, что, по свидетельству известных специалистов в области портфельных инвестиций Э. Элтона и М. Грубера, исследования в этой области в последующие сорок лет сводились в основном к разработке методов применения базовых идей и концепций теории Марковича. Очевидно, что эффективных портфелей может быть построено много, поэтому вводится понятие «оптимальный портфель». Основная идея определения оптимального портфеля в рамках теории Марковича может быть описана следующим образом. Инвестор строит для себя набор кривых безразличия, т.е. кривых, отражающих различные комбинации доходности и риска. Считается, что чем выше расположена кривая, тем выше и уровень удовлетворенности, достигаемый инвестором. Все комбинации, находящиеся на некоторой кривой безразличия, равноприемлемы для инвестора, т.е. он безразличен к выбору конкретной комбинации из набора. Далее строится набор эффективных портфелей (имеется в виду, что если инвестор имеет на выбор два портфеля одинакового риска, но с разной доходностью, то портфель, имеющий большую доходность, и будет эффективным). Оптимальным для инвестора будет портфель, характеризующийся точкой пересечения множества эффективных портфелей и одной из кривых безразличия. Любое предприятие может рассматриваться как совокупность некоторых активов (материальных и финансовых), находящихся в определенном сочетании. Владение любым из этих активов связано с определенным риском в плане воздействия этого актива на величину общего дохода предприятия. То же самое в полном объеме относится к портфелям ценных бумаг, причем, как было отмечено выше, степень риска изменяется обратно пропорционально количеству включенных в портфель случайным образом видов ценных бумаг. Общий риск портфеля состоит из двух частей: диверсифицируемый (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестиривание 1 млн. руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании); недиверсифицируемый (систематический, или рыночный) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля. Р 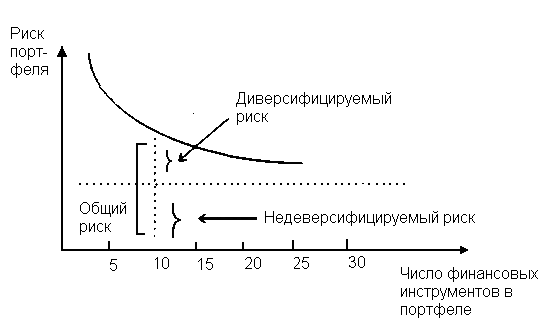 ис. 3.3. – Зависимость степени риска от диверсификации портфеля Исследования показали, что если портфель состоит из 10–20 различных видов ценных бумаг, включенных в портфель с помощью случайной выборки из имеющегося на рынке ценных бумаг набора то несистематический риск может быть сведен к минимуму (это показано и на рис. 3.3.). Таким образом, этот риск поддается элимированию довольно несложными методами, поэтому основное внимание следует уделять возможному уменьшению систематического риска. Как отмечалось выше, существует «теория портфеля» (portfolio theory)–теория финансовых инвестиций, в рамках которой с помощью статистических методов и осуществляются наиболее выгодно распределение риска портфеля ценных бумаг и оценка прибыли, теория состоит из четырех основных элементов: оценка активов (security valuation); инвестиционные решения (asset allocation decision); оптимизация портфеля (portfolio optimization); оценка результатов (performance measurement). В процессе управления инвестиционным портфелем менеджер постоянно сталкивается с задачей отбора новых инструментов и анализа возможности их включения в портфель. Какими же методами можно это делать? Существует несколько способов, однако наибольшую известность получила модель оценки доходности финансовых активов (CapitalAssetPricingModel, САРМ), увязывающая систематический риск и доходность портфеля. Как и любая теория финансов, модель САРМсопровождается рядом предпосылок, которые в акцентированном виде были сформулированы М. Дженсеном и опубликованы им в 1972 г. Эти предпосылки таковы. Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и среднеквадратических отклонений альтернативных инвестиционных портфелей. Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке krf, при этом не существует ограничений на «короткие» продажи любых активов. Все инвесторы одинаково оценивают величину ожидаемых значений доходности, дисперсии и ковариации всех активов; это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей. Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут быть проданы на рынке по существующей цене). Не существует трансакционных расходов. Не принимаются во внимание налоги. Все инвесторы принимают цену как экзогенно заданную величину (т. е. они полагают, что их деятельность по покупке и продаже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг). Количество всех финансовых активов заранее определено и фиксировано. Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер и не могут быть выполнены на практике. Для понимания логики модели легче всего воспользоваться графическим представлением (рис. 3.4.). Ставится задача найти взаимосвязь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x). Построение основывается на следующих очевидных рассуждениях: а) доходность ценной бумаги связана с присущим ей риском прямой связью; б) риск характеризуется некоторым показателем β в) «средней» ценной бумаги, т.е. бумаги, имеющей средние значения риска и доходности, соответствуют β = 1 и доходность km; г) имеются безрисковые ценные бумаги со ставкой kти β = 0. Исходя из приведенных выше предпосылок доказывается, что искомая зависимость y =f(x) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, krf) и (1, km). Из курса геометрии известно, что уравнение прямой, проходящей через точки (x2,y2) и (x1,y1), задается формулой 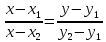 , (3.27.) , (3.27.)Подставляя в формулу исходные данные, получим: y = 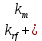 -krf)×x, (3.28.) -krf)×x, (3.28.)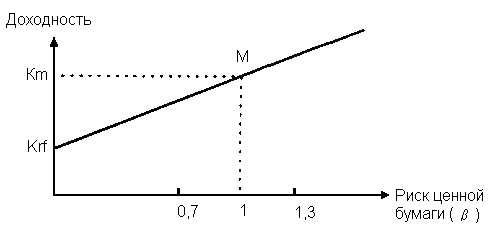 Рис. 3.4. – Логика представления модели САРМ Имея в виду, что переменная х представляет собой риск, характеризуемый показателем β, а у — ожидаемую доходность ke, получим следующую формулу, которая и представляет собой модель CAMP: ke = krf+β×(km – krf), (3.29.) где ke - ожидаемая доходность акций данной компании; krf- доходность безрисковых ценных бумаг (в частности, в США берут за основу государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка); km - ожидаемая доходность в среднем на рынке ценных бумаг; β - бета-коэффициент данной компании. Показатель (km - krf) имеет вполне наглядную интерпретацию представляя собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпорации и пр.). Аналогично показатель (ke -krf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании. Модель CAMP означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск. Модель CAMP позволяет спрогнозировать доходность финансового актива; в свою очередь, зная этот показатель и имея данные об ожидаемых доходах по этому активу, можно рассчитать его теоретическую стоимость. Систематический риск в рамках модели CAMP измеряется с помощью β-коэффициентов (бета-коэффициентов). Каждый вид ценной бумаги имеет собственный β-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя β рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специальных справочниках. Для каждой компании β меняется с течением времени и зависит от многих факторов, в частности имеющих отношение к характеристике деятельности компании с позиции долгосрочной перспективы. Очевидно, что сюда относится, прежде всего показатель уровня финансового левериджа, отражающего структуру источников средств: при прочих равных условиях, чем выше доля заемного капитала, тем более рисковая компания и тем выше ее β. Например, имеется совокупность показателей доходности по группе компаний за ряд периодов {kij}, где: kij - показатель доходности i-й компании (i = 1,2,... ,t) в j-м периоде (j = 1,2,...,n). Тогда общая формула расчета β-коэффициента для произвольной i-й компании имеет вид: βi = 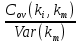 , (3.30.) , (3.30.)где Cov(ki, km) = 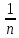 * *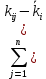 )*( )*(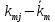 ) ; ) ;Var( 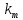 )= )= 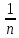 * *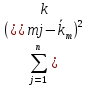 ; ;kmj = 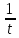 * *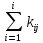 - доходность в среднем на рынке ценных бумаг в j-м периоде; - доходность в среднем на рынке ценных бумаг в j-м периоде;km = 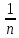 * *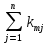 – доходность в среднем на рынке ценных бумаг за все периоды; – доходность в среднем на рынке ценных бумаг за все периоды;ki = 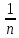 * *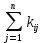 - доходность ценных бумаг i-и компании в среднем за все периоды. - доходность ценных бумаг i-и компании в среднем за все периоды.В целом по рынку ценных бумаг β-коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство β-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация β-коэффициента для акций конкретной компании заключается в следующем: β= 1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом; β < 1 означает, что ценные бумаги данной компании менее рискованны, чем в среднем на рынке (так, β = 0,5 означает, что данная ценная бумага в два раза менее рискованна, чем в среднем на рынке); β > 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке; увеличение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованны. снижение β -коэффициента в динамике означает, что вложенные ценные бумаги данной компании становятся менее рискованны. В качестве примера можно привести усредненные данные о β-коэффициентах ряда американских компаний в 1987—1991 гг.: наивысшие значения β -коэффициентов имели компании: American Express – 1,5; Bank America – 1,4; Chrysler – 1,4. средние значения β -коэффициентов имели компании: Digital Equipment Со – 1,1; Walt Disney –0,9; DuPont –1,0. наименьшие значения β -коэффициентов имели компании: General Mills – 0,5; Gillette – 0,6; Southern California Edison – 0,5. Следует отметить, что единого подхода к исчислению β-коэффициентов, в частности в отношении количества и вида исходных наблюдений, не существует. С 1995 г. β - коэффициенты появились и на отечественном pынке ценных бумаг. Расчеты выполняются информационно-аналитическим агентством «Анализ, консультация и маркетинг» (АК&М), однако список компаний, как правило, не превышает полутора десятков, охватывая в основном предприятия энергетики и нефтегазового комплекса. Значения β - коэффициентов достаточно ощутимо варьируют. Для наглядности логика взаимосвязи рассмотренных показателей может быть объяснена с помощью графика, носящего название линии рынка ценных бумаг (Security Market Line, SML).График SMLотражает линейную зависимость «доходность/риск» для конкретных ценных бумаг и выглядит следующим образом (рис. 3.5). 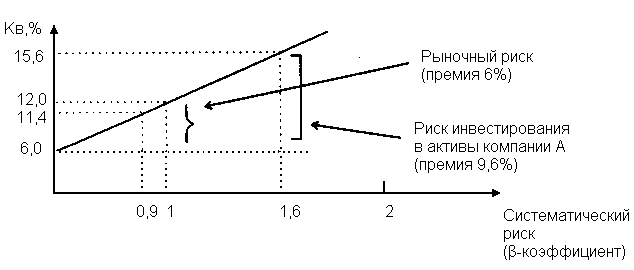 Рис. 3.5. – График линии рынка ценных бумаг Важным свойством модели CAMPявляется ее линейность относительно степени риска. Это дает возможность определять β -коэффициент портфеля как средневзвешенную β -коэффициентов входящих в портфель финансовых активов. βp = 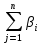 *di, (3.31.) *di, (3.31.)где β i - значение бета-коэффициента i-го актива в портфеле; βp -значение бета-коэффициента портфеля; di - доля i- гo актива в портфеле; n - число различных финансовых активов в портфеле Обобщением понятия «линия рынка ценных бумаг» является линия рынка капитала (Capital Market Line, CML), отражающая зависимость (доходность/риск) для эффективных портфелей, которые, как правило, сочетают безрисковые и рисковые активы. Линию рынка капитала можно использовать для сравнительного анализа портфельных инвестиций. Как следует из модели CAMP, каждому портфелю соответствует точка в квадранте на рис. 3.4. Возможны три варианта расположения этой точки: на линии рынка капитала ниже или выше этой линии. В первом случае портфель называется эффективным, во втором – неэффективным, в третьем – сверхэффективным. Известны и другие способы применения линии рынка капитала. В частности, отбирая финансовые активы в портфель, инвестор может находить, какой должна быть доходность при заданном уровне риска. Как отмечено выше, модель CAMP разработана исходя из ряда предпосылок, часть из которых не выполняется на практике, например налоги и трансакционные затраты существуют, инвесторы находятся в неравных условиях, в том числе и в отношении доступности информации и т.п. Поэтому модель не является идеальной и неоднократно подвергалась как критике, так и эмпирической проверке. Особенно интенсивно исследования в этом направлении велись с конца 60-x годов, а их результаты нашли отражение в сотнях статей. Существуют различные точки зрения по поводу модели, поэтому приведем некоторые наиболее типовые представления о современном состоянии этой теории из обзора, сделанного Ю.Бригхемом и Л.Гапенски. 1. Концепция CAMP, в основе которой лежит приоритет рыночного риска перед общим, является весьма полезной, имеющей фундаментальное значение в концептуальном плане. Модель логично отражает поведение инвестора, стремящегося максимизировать свой доход при заданном уровне риска и доступности данных. 2. Теоретически CAMP дает однозначное и хорошо интерпретируемое представление о взаимосвязи между риском и требуемой доходностью, однако она предполагает, что для построения связи должны использоваться априорные ожидаемые значения переменных, тогда как в распоряжении аналитика имеются лишь апостериорные фактические значения. Поэтому оценки доходности, найденные с помощью модели, потенциально содержат ошибки. 3. Некоторые исследования, посвященные эмпирической проверке модели, показали на значительные отклонения между фактическими и расчетными данными, что позволило ряду ученых подвергнуть эту теорию серьезной критике. В частности, к ним относятся Ю.Фама и К.Френч, которые изучили зависимость между β-коэффициентами и доходностью нескольких тысяч акций по данным за пятьдесят лет. По мнению Бригхема и Гапенски, модель CAMPописывает взаимосвязи между ожидаемыми значениями переменных, поэтому любые выводы, основанное на эмпирической проверке статистических данных, вряд ли правомочны и не могут опровергнуть теорию. Тем не менее, многие ученые понимает, что один из основных недостатков модели заключается в том, что она является однофакторной. Указывая на этот недостаток, известные специалисты Дж. Уэстон и Т. Коуплэнд приводят такой образней пример. Представьте себе, что ваш маленький самолет не может совершить посадку из-за сильного тумана, и на вопрос диспетчерам о помощи вы получите информацию о том, что самолет находится в ста милях от посадочной полосы. Конечно, информация весьма полезна, но вряд ли достаточна для успешной посадки. 3.8. Теория ценообразования опционов Основой для разработки теории реальных опционов стал финансовый опцион. Финансовый опцион – это ценная бумага, торгующаяся на бирже, которая дает своему владельцу право купить или продать в течение установленного срока определенное число акций или других ценных бумаг по заранее зафиксированной цене. В приведенной таблице 3.1. представлена эквивалентность реальных и финансовых опционов. Таблица 3.1. Сравнение финансового и реального опционов
Терминологию реальных опционов разработал Стефен Марглин. В 1970 году он описал понятие реальных опционов (real-estate options) следующим образом: «Когда частные инвесторы имеют монопольную власть в некотором инвестиционном секторе, право осуществлять проект становится экономическим объектом, имеющим определенную ценность, независимо от самого процесса инвестирования. В принципе, нет препятствий для того, чтобы такое право было куплено или продано, хотя рынки для таких прав скорее исключение из правил. Реальные опционы являются особым случаем формального инструмента, который определяет соотношение между правом на осуществление инвестиций и самим инвестированием. Обычно само такое соотношение гораздо менее формально, положение на рынке или особые знания создают скрытые опционы, связанные с определенными инвестициями, опционы, для которых не существует рынков, но которые от этого не менее реальны». Понятие реального опциона детерминируют как право его владельца, но не обязательство, на совершение определенного действия в будущем. Финансовые опционы предоставляют право покупки (продажи) определенного базисного актива и страхуют финансовые риски. Реальные опционы дают право на изменение хода реализации проекта и страхуют стратегические риски. Как правило, реальные опционы отождествляют с определенным активом компании, например патентом или лицензией. Патент или лицензия на продукт обеспечивают фирме право на развитие продукта и его рынка. Обладая патентом, фирма может в любой благоприятный момент начать реализацию продукта, совершив начальные инвестиции в его развитие. «Реальные опционы», их распознавание, понимание и иногда оценка есть не что иное, как спектр методов гибкого использования активов и пассивов предприятия. Многие инвестиционные проекты содержат различные виды опционов. К примеру, компания рассматривает возможность приобретения лицензии на разработку месторождения нефти на конкретном участке земли. Но на данный момент стоимость добычи нефти в этом месте не окупится доходами от ее реализации, поэтому такой проект выглядит убыточным. С другой стороны, принимая во внимание, что цены на нефть на мировом рынке подвержены серьезным колебаниям, несложно предположить, что через год или два они резко вырастут и разработка месторождения принесет значительные прибыли. В таком случае лицензия на разработку нефти дает компании право, но не обязательство реализовать проект, если условия для этого будут благоприятны. Другими словами, покупая лицензию, компания приобретает реальный опцион. В отличие от DCF-модели (дисконтированных денежных потоков), который учитывает только поступление и расход денежных средств, метод реальных опционов позволяет учесть большее количество факторов. К ним относятся: период, в течение которого сохраняется инвестиционная возможность, неопределенность будущих поступлений, текущая стоимость будущего поступления и расходования денежных средств стоимость, теряемая во время срока действия инвестиционной возможности. Таким образом, использование реальных опционов обеспечивает всестороннюю оценку стратегического решения даже при наличии неопределенности. Применение методики реальных опционов к оценке инвестиционных проектов целесообразно, когда выполняются следующие условия: результат проекта подвержен высокой степени неопределенности; менеджмент компании способен принимать гибкие управленческие решения при появлении новых данных по проекту; финансовый результат проекта во многом зависит от принимаемых менеджерами решений. При оценке проекта по методу дисконтированных денежных потоков значение ЧДД отрицательно или чуть больше нуля. Таким образом, метод ROV (реальных опционов) не претендует на полное замещение DCF-модели (дисконтированных денежных потоков). Фактически оценка реальных опционов использует DCF-модели как один из его инструментов. При этом подходе неопределенность остается, а оператор проекта с течением времени подстраивается (принимает оптимальные решения) к изменяющейся ситуации. Иначе говоря, реальные опционы дают возможность изменять и принимать оптимальные решения в будущем в соответствии с поступающей информацией. Будущее расценивается как совокупность альтернатив и выборов (опционов), которые могут добавлять стоимость. В концепции ROV стоимость реального опциона складывается из стандартной величины ЧДД, рассчитанной по DCF-модели , и так называемой "стоимости гибкости", в результате чего образуется полная стоимость проекта (рис.3.6). "Стоимость гибкости" обусловлена существованием определенной ценности развития инвестиционного проекта, получением новой, более достоверной информации, на основе которой можно улучшить как промежуточные, так и конечные результаты. Перечисленные позитивные условия снижают степень неопределенности.  Рис. 3.6. Формирование полной стоимости проекта Методы оценки стоимости реальных опционов Для оценки стоимости реальных опционов используются два основных метода: модель оценки стоимости опционов Блэка—Шоулза; биномиальная модель. Модель оценки стоимости опционов Блэка—Шоулза Данная модель проста как в изложении, так и в применении. Однако она имеет ряд ограничений: оцениваемый актив должен быть ликвидным (необходимо наличие рынка для оцениваемого актива); изменчивость цены актива остается одинаковой (то есть не происходит резких скачков цен); опцион не может быть реализован до срока его исполнения (европейский опцион). Рассмотри подробнее модель Блэка-Шоулза. Текущая цена опциона определяется согласно формуле: C0=S0*N(d1)-X*e-r*t*N(d2), (3.32.) d1= 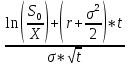 , (3.33.) , (3.33.)d2=d1-σ* 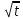 (3.34.) (3.34.)где S0 текущая цена опциона; S0 - текущая цена базового актива. Предполагается, что актив не приносит текущего дохода (дивиденда, купона); Х - цена исполнения опциона; e - основание натурального логарифма (е=2,718); r - ставка безрисковой доходности, исчисленная по способу непрерывных процентов: r=ln(1+rf), (3.35.) где rf - годовая ставка безрисковой доходности, доли ед.; t - время до исполнения опциона; σ - среднеквадратическое отклонение цены базисного актива за год, доли ед.; N(d) - кумулятивная функция нормального распределения. Биномиальная модель Техника построения биномиальной модели является более громоздкой, чем метод Блэка—Шоулза, но позволяет получить более точные результаты, когда существует несколько источников неопределенности или большое количество дат принятия решения. В основе модели лежат два допущения: в одном интервале времени могут быть только два варианта развития событий (худший и лучший); инвесторы нейтрально относятся к риску. Биномиальный метод внешне схож с методом «дерева решений». Однако эти два метода работают по-разному. Метод «дерева решений» требует, чтобы аналитик определил вероятности и соответствующие нормы дисконта в каждом узле, что усиливает субъективность решения задачи. Метод ROV использует вероятность, при которой инвесторы безразличны к риску, а также безрисковую норму процента. Обе величины более объективны по своему содержанию и результат получается более точным. Основное различие между моделями состоит в том, что одна является дискретной и предполагает наличие заранее известного конечного числа интервалов (звеньев) бинарного дерева, а другая – непрерывной и основывается на том, что число звеньев дерева бесконечно велико, а длина каждого интервала соответственно бесконечно мала. Таким образом, биномиальная модель требует построения двух сеток: сетки изменения значений базисного актива и сетки расчета стоимости опциона. С целью получения значения опциона требуется расчет следующих параметров. Фактор роста определяется исходя из следующей формулы: u = 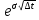 , (3.36.) , (3.36.)где ∆t - время шага: ∆t = 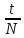 , (3.37.) , (3.37.)где N - число шагов биномиальной модели. Фактор снижения определяется: d = u-1, (3.38.) Поскольку при переходе от одного звена биномиального дерева к другому риск проекта меняется, вместе с ним должна корректироваться и ставка дисконтирования. Однако обосновать значение ставок дисконтирования в каждом узле с практической точки зрения является задачей затруднительной, поэтому прибегают к использованию риск-нейтральных вероятностей, которые являются лишь посредниками в расчете стоимости реальных опционов при применении метода обратной индукции и не несут практического финансового или экономического смысла. Риск-нейтральные вероятности рассчитываются в соответствии с формулами (8), (9). Pu = 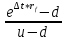 , (3.39.) , (3.39.)Pd = 1- Pu, (3.40.) Поясним строение биномиальной решетки на следующем примере: ∆t=1 год, t=5 годам. Сначала биномиальная решетка заполняется в прямом порядке, а после – в обратном (рис. 3.7.). 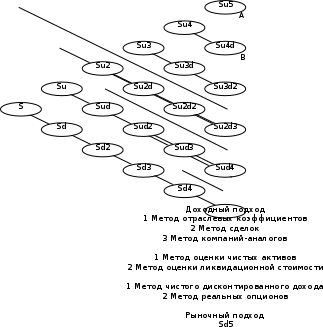 Рис. 3.7. – Биномиальная решетка В последнем периоде биномиальной сетки при обратном заполнении используются правила max (S-X;0). Стоимость реального опциона S находится следующим образом: S = (Pu*A+Pd*B)* 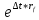 , (3.41.) , (3.41.)Основные трудности, которые могут возникнуть при применении этой модели, связаны с получением достоверных исходных данных, необходимых для расчета (время до реализации заложенных в проекте возможностей, значение дисперсии и т. д.). Таким образом, формула Блэка—Шоулза подходит для оценки простых реальных опционов, имеющих единственный источник неопределенности и единственную дату решения. Вопросы для самопроверки Назовите виды финансовых активов. Назовите показатели стоимостной оценки облигации. Дайте смысловую трактовку текущей доходности. Дайте смысловую трактовку капитализированной доходности. Что такое портфель ценных бумаг? На основании каких инвестиционных характеристик классифицируются инвестиционные портфели? Чем отличается фундаментальный анализ оценки качества ценной бумаги от технического? Назовите виды доходности фондовых портфелей? |
