Корпоративные финансы ( лекции). Учебное пособие Направление подготовки магистры Уфа 2017 Содержание Введение стр

• Название: Учебное пособие Направление подготовки магистры Уфа 2017 Содержание Введение стр
• Дата: 21.04.2022
• Размер: 0.73 Mb.
• Имя файла: Корпоративные финансы ( лекции).docx
• Тип: Учебное пособие; #489319
• страница: 10 из 17

Оценка облигаций с нулевым купоном

Поскольку денежные поступления по годам, за исключением последнего года, равны нулю, формула имеет вид:

V_t = 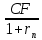= CF×FM2(r,n) , (3.4.)

где V_t - стоимость облигации с позиции инвестора (теоретическая стоимость);

CF - сумма, выплачиваемая при погашении облигации;

n - число лет, через которое произойдет погашение облигации;

FM2(r, n) - дисконтирующий множитель из финансовой таблицы.
Оценка бессрочных облигаций

Бессрочная облигация предусматривает неопределенно долгую выплату дохода (CF) в установленном размере или по плавающей процентной ставке. В первом случае формула (3.1) преобразуется в формулу суммы членов бесконечно убывающей геометрической прогрессии:

V_t = 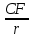, (3.5.)
Оценка безотзывных облигаций с постоянным доходом

Денежный поток в этом случае складывается из одинаковых по годам поступлений (С) и нарицательной стоимости облигации (М), выплачиваемой в момент погашения. Таким образом, формула (1) преобразуется в следующую:

V_t = C×∑( 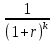) + 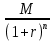= C×FM2(r,n) + M×FM4(r,n) , (3.6.)

где FM2(r,n) и FM4(r,n) дисконтирующие множители из финансовых таблиц.
В экономически развитых странах весьма распространенными являются облигационные займы с полугодовой выплатой процентов. Такие займы более привлекательны, поскольку инвестор в этом случае в большей степени защищен от инфляции и, кроме того, имеет возможность получения дополнительного дохода от реинвестирования получаемых процентов.

Преобразовав формулу (4), можно дать общую формулу для расчета внутренней стоимости облигации с выплатой процента каждые полгода:

V_t = 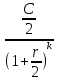+ 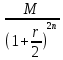, (3.7.)

Относительно поведения цены облигации на рынке ценных бумаг можно сделать следующие выводы:

• 
  если рыночная норма прибыли превосходит фиксированную купонную ставку, облигация продается со скидкой (дисконтом), т.е. по цене ниже номинала;
  
• 
  если рыночная норма прибыли меньше фиксированной купонной ставки, облигация продается с премией, т.е. по цене выше номинала (разница между рыночной ценой и номиналом носит название «ажио»);
  
• 
  если рыночная норма прибыли совпадает с фиксированной купонной ставкой, облигация продается по нарицательной стоимости;
  
• 
  рыночная норма прибыли и текущая цена облигации с фиксированной купонной ставкой находятся в обратно пропорциональной зависимости – с ростом (убыванием) рыночной нормы прибыли текущая цена такой облигации убывает (возрастает).
  

Оценка отзывных облигаций с постоянным доходом

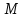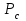Отзывная облигация отличается от безотзывной наличием двух дополнительных характеристик: выкупной цены и срока защиты от досрочного погашения. Оценка подобных облигаций осуществляется также с использованием формул, в которых нарицательная стоимость заменена выкупной ценой . В период, когда облигация защищена от досрочного погашения, оценка ее текущей внутренней стоимости может варьировать не только в зависимости от закладываемой в расчет приемлемой нормы прибыли, но и от того, с какой вероятностью оценивает аналитик возможность досрочного погашения.
3.4. Оценка долевых ценных бумаг

Долевыми ценными бумагами являются различные виды акций. Различают несколько количественных характеристик, используемых для оценки акций: внутренняя, номинальная, балансовая, конверсионная и ликвидационная стоимости, а также эмиссионная и курсовая цены.

Внутренняя стоимость представляет собой расчетный показатель, исчисляемый по формуле (3.4). Конверсионную стоимость можно рассчитывать для привилегированных акций в условиях эмиссии, которых предусмотрена возможность их конвертации в обыкновенные акции.

Номинальная стоимость акции – это стоимость, указанная на бланке акции. В отличие от облигации, для которой номинальная стоимость имеет существенное значение, поскольку проценты по облигациям устанавливаются по отношению к номиналу независимо от курсовой цены, для акции этот показатель практически не имеет значения и несет лишь информационную нагрузку, характеризуя долю уставного капитала, которая приходилась на одну акцию в момент учреждения компании.

Эмиссионная цена представляет собой цену, по которой акция эмитируется, т.е. продается на первичном рынке. Эта цена может отличаться от номинальной стоимости, поскольку чаще всего размещение акций производится через посредническую фирму, являющуюся профессиональным участником фондового рынка. В этом случае посредническая фирма скупает весь выпуск акций по согласованной цене и в дальнейшем реализует их на рынке по цене, которая определяется уже этой фирмой и, естественно, превышает номинал.

С началом операций компании доля капитала, приходящаяся на одну акцию, немедленно меняется. С этой точки зрения акция характеризуется балансовой стоимостью, которая может быть рассчитана по балансу как отношение стоимости чистых активов (общая стоимость активов по балансу за минусом задолженности кредиторам) к общему числу выпущенных акций.

Ликвидационная стоимость акции может быть определена лишь в момент ликвидации общества. Она показывает, какая часть стоимости активов по ценам возможной реализации, оставшаяся после расчетов с кредиторами, приходится на одну акцию. Поскольку учетные цены активов могут значительно отличаться от их рыночных цен в зависимости от инфляции и конъюнктуры рынка, ликвидационная стоимость не равна балансовой.

Для учета и анализа наибольшее значение имеет курсовая (текущая рыночная) цена. Именно по этой цене акция котируется (оценивается) на вторичном рынке ценных бумаг. Курсовая цена зависит от разных факторов: конъюнктуры рынка, рыночной нормы прибыли, величины и динамики дивиденда, выплачиваемого по акции и др. Она может определяться различными способами, однако в основе их лежит один и тот же принцип – сопоставление дохода, приносимого данной акцией, с рыночной нормой прибыли. В качестве показателя дохода можно использовать либо дивиденд, либо величину чистой прибыли, приходящейся на акцию.

Оценка целесообразности приобретения акций, как и в случае с облигациями, предполагает расчет теоретической стоимости акции и сравнение ее с текущей рыночной ценой.

Привилегированные акции, как и бессрочные облигации, генерируют доход неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле (3.1). Таким образом, наиболее простым вариантом оценки привилегированной акции является отношение величины дивиденда к рыночной норме прибыли по акциям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск).

В некоторых странах привилегированные акции нередко эмитируются на условиях, позволяющих эмитенту выкупить их в определенный момент времени по соответствующей цене, называемой ценой выкупа (call price). В этом случае текущая теоретическая стоимость таких акций определяется по формуле (3.7), где M заменяется ценой выкупа P_c. Эмиссия бессрочных привилегированных акций, предусматривающих выплату дивиденда по постоянной ставке, является довольно рисковым мероприятием, поскольку невозможно спрогнозировать процентные ставки на длительную перспективу. Именно поэтому условиями выпуска привилегированных акций нередко принимается во внимание их конверсия в обыкновенные акции.

Известны различные методы оценки обыкновенных акций, наиболее распространенным из них является метод, основанный на оценке их будущих поступлений, т.е. на применении формулы (3.4), которая меняется в зависимости от предполагаемой динамики дивидендов. Базовыми являются три варианта динамики прогнозных значений дивидендов:

• 
  дивиденды не меняются (применяется формула (3.6));
  
• 
  дивиденды возрастают с постоянным темпом прироста;
  
• 
  дивиденды возрастают с изменяющимся темпом прироста.
  

Оценка акций с равномерно возрастающими дивидендами

Предполагается, что базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна C; ежегодно она увеличивается с темпом прироста g. Например, по окончании первого года периода прогнозирования будет выплачен дивиденд в размере C×(1+g) и т.д. Тогда формула (3.4) имеет вид:

V_t = 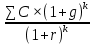= C×∑q^k , (3.8.)

где q = .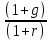
Домножив обе части (3.7.) на q и вычтя новое уравнение из (3.8.), получим:

V_t ×(1-q) = C×q, (3.9.)

Таким образом:

V_t = 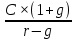, (3.10)

Данная формула имеет смысл при r > g и называется моделью Гордона. Отметим, что показатели r и g в этой и последующих формулах берутся в долях единиц. Очевидно, что числитель формулы (3.10) представляет собой первый ожидаемый дивиденд фазы постоянного роста.
Оценка акций с изменяющимся темпом прироста

Из формулы (3.10.) видно, что текущая цена обыкновенной акции очень чувствительна к параметру g. Даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подинтервалы, каждый из которых характеризуется собственным темпом прироста g. Так, если выделить два подинтервала с темпами прироста g и p соответственно, то формула (3.4.) принимает вид:

V_t = 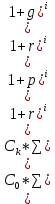, (3.11.)

где C_o - дивиденд, выплаченный в базисный момент времени;

C_k- прогноз дивиденда в k - м периоде;

g- прогноз темпа прироста дивиденда в первые k подпериодов;

p - прогноз темпа прироста дивидендов в последующие подпериоды.

Главная сложность этой модели состоит в выделении подпериодов, прогнозировании темпов прироста (как правило, в прогнозах темпы прироста в динамике снижаются) и коэффициентов дисконтирования для каждого подпериода. При выделении нескольких подпериодов модель становится более громоздкой в представлении, однако вычислительные процедуры достаточно просты. Безусловно, модель должна рассматриваться в динамике и постоянно уточняться по мере получения новой информации, в частности по истечении очередного подпериода.

В теории и практике оценки акций описана и получила достаточно широкое распространение ситуация, когда темп прироста дивидендов в течение нескольких лет прогнозного периода меняется (фаза непостоянного роста), однако по истечении этих лет он устанавливается на некотором постоянном уровне. Считается, что такое развитие событий характерно для компаний, находящихся в стадии становления, либо уже зрелых компаний, осваивающих новые виды продукции или перспективные рынки сбыта. Тогда в течение непродолжительного подпериода темп прироста может быть сравнительно высоким, причем не обязательно одинаковым, а затем он снижается и становится постоянным. Наиболее общая постановка задачи в этом случае такова.

Пусть продолжительность фазы непостоянного роста составляет k лет, дивиденды в этот период по годам равны C_j, j = 1,2,…,k. C_k+1 – первый ожидаемый дивиденд фазы постоянного роста с темпом g; r – приемлемая норма прибыли. Схематично данная ситуация выглядит следующим образом.
C₁ C₂ … C_k-1 C_k C_k+1 C_k+2 C_k+3 C_k+4 C_k+5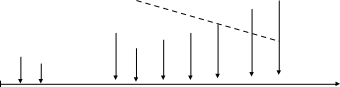



1 2 … k-1 k k+1 k+2 k+3 k+4 k+5 Годы

Рис.3.2. – Изменение дивидендных выплат
Из приведенной схемы видно, что в первые k лет прогнозируется бессистемное изменение величины годового дивиденда, а начиная с момента 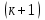, эта величина равномерно увеличивается, т.е.

C_k+1 = C_k×(1+g); C_r+2 = C_k+1×(1+g) = C_k×(1+g)² т.д. (3.12.)

Тогда на основании формулы (3.10) второе слагаемое в формуле (3.11) будет иметь вид:

V_tk = 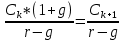, (3.13.)

Показатель V_tk дает оценку акции на конец периода k. Поскольку мы пытаемся сделать оценку с позиции начала первого года, значение V_tk нужно дисконтировать. Таким образом, формула (3.11), позволяющая рассчитать теоретическую стоимость акции на конец года 0, может быть трансформирована следующим образом:

V_t = ∑ 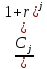+ 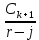× 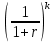, (3.14.)

3.5. Доходность финансового актива: виды и оценка

Доходность – это относительный показатель, рассчитываемый соотнесением дохода (D), генерируемого данным финансовым активом, и величины инвестиций (CI) в этот актив, т.е. в наиболее общем виде он может быть представлен следующим образом:

K= 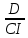, (3.15.)

В зависимости от вида финансового актива в качестве дохода чаще всего выступают дивиденд, процент, прирост капитализированной стоимости. Поэтому существуют различные варианты расчета доходности. Этот показатель измеряется в процентах или долях единицы; первый измеритель используется для вербальной, или описательной, характеристики финансового актива, второй – при проведении расчетов.

В анализе речь может идти о двух видах доходности – фактической и ожидаемой. Первая рассчитывается post factum и имеет значение лишь для ретроспективного анализа. Ожидаемая доходность рассчитывается на основе прогнозных данных в рамках имитационного перспективного анализа и используется для принятия решения о целесообразности приобретения тех или иных финансовых активов.

Приобретая некий финансовый актив, например акции, инвестор вправе рассчитывать на два вида потенциальных доходов: а) дивиденд; б) доход от прироста капитала. Оба поступления не являются безусловными и могут состояться, как правило, в случае эффективной работы компании, чьи акции приобретены. Оговорка «как правило» сделана потому, что, например, динамика дивидендов и прибыли совершенно не обязаны совпадать. Так, многие компании в экономически развитых странах нередко считают целесообразным выплатить дивиденды даже в том случае, если отчетный год закончен с убытком. Причина такой на первый взгляд нелогичной политики заключается в том, чтобы избежать нежелательных последствий сигнального эффекта негативной информации.

Введем следующие обозначения.

P₀ P₁

... D₀ D₁ …

t₀ t₁ Время

В отношении приведенных на схеме показателей считается, что цена финансового актива, приобретенного (или возможного к приобретению по желанию инвестора) в некоторый момент времени t₀, когда и проводится анализ, определенно известна и равна P_o; известен и регулярный доход D₀ в виде процентов или дивидендов, полученных за период, истекший в момент времени t₀; ожидается, что за следующий период (t_0, t₁) регулярный доход составит величину D₁; по истечении данного периода актив может быть реализован по цене P₁ (ожидаемая величина). Величина (P₁ – P₀) как раз и представляет собой доход от прироста капитала (или доход от капитализации). Итак, в данной схеме в отношении D₀ и P₀ известны их фактические значения, 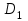представляет собой исходную прогнозную оценку, а P₁ является целевым расчетным показателем. Обычно считается, что P₁>P₀, хотя в принципе выполнение этого неравенства не является обязательным, и в этом случае говорят об убытке от капитализации и соответствующей ему отрицательной доходности. Таким образом, общий доход, генерируемый инвестициейP₀, за данный период (t_0, t₁) составит величину: D₁+(P₁ – P₀), а общая доходность (k_t) будет равна:

k_t = 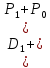= 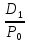+ 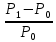= 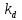+ 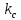, (3.16.)

Первое слагаемое (k_t) представляет собой текущую доходность (в приложении к акциям она называется также дивидендной); второе слагаемое (k_c) носит название капитализированная доходность. Из приведенной формулы хорошо видно, что общий доход (общая доходность) имеет два компонента, причем в зависимости от успешности работы и стратегии развития компании, эмитировавшей данный актив, весомость того или иного компонента может быть различной. Таким образом, выбирая для покупки акции той или иной компании, инвестор должен расставить для себя приоритеты – что важнее, дивиденды или доход от прироста капитала. Вычислительные алгоритмы этой теории базируются на формуле (3.2).

Если предположить, что рынок ценных бумаг является эффективным и находится в состоянии равновесия, то в отношении конкретного финансового актива в любой момент времени известны его текущая цена и доходы, которые, как ожидается, этот актив будет генерировать в будущем. Зная эти оценки, можно разрешить уравнение (3.2) относительно параметра r, полученное значение которого и можно трактовать как общую доходность данного актива.

В зависимости от вида финансового актива и абсолютных показателей, выбранных для его характеристики, можно исчислить несколько числовых характеристик доходности. Поскольку их значения могут существенно различаться, нельзя говорить о некой абстрактной доходности, необходимо обязательно уточнять, о чем идет речь, какой алгоритм используется для расчета.