Логистика практикум. Учебное пособие практически задачи, примеры решения, варианты для самостоятельной работы, тесты Москва 2009 ббк 330 (075. 8) Д53
 Скачать 1.94 Mb. Скачать 1.94 Mb.
|
|
Глава 4. Управление запасами Образование запасов связано с необходимостью обеспечения непрерывности процесса производства на всех его стадиях. Питание производства должно осуществляться регулярно. Поэтому от наличия и состояния запасов в первую очередь зависит ритмичная работа предприятия. Управление запасами предполагает решение двух задач: определение размера необходимого запаса (нормы запаса); контроль за фактическим размером запаса и его изменением в соответствии с расчетной нормой. Задача 1 План годового выпуска продукции производственного предприятия составляет 800 единиц, при этом на каждую единицу готовой продукции требуется 2 единицы комплектующего изделия КИ-1. Известно, что стоимость подачи одного заказа составляет 200 руб., цена единицы комплектующего изделия — 480 руб., а стоимость содержания комплектующего изделия на складе составляет 15% его цены. Требуется определить оптимальный размер заказа на комплектующее изделие КИ-1. Решение Затраты на содержание запасов в определенный период складываются, из следующих элементов: 1) суммарная стоимость подачи заказов; 2) цена заказываемого комплектующего изделия; 3) стоимость хранения запаса. Таким образом, графически уровень суммарных издержек в зависимости от размера заказа может быть представлен следующим образом (см. рис. 4.1). 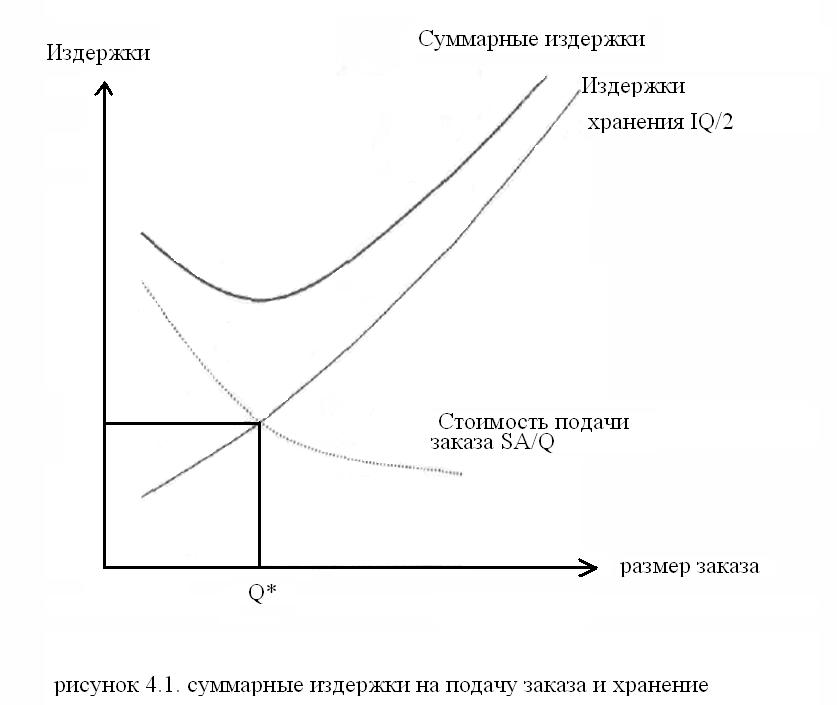 Рис 4.1. Суммарные издержки на подачу заказа и хранение I – затраты на содержание еденицы запаса, руб./шт.; Q – размер заказа, шт.; Q* - оптимальный размер заказа, шт.; А – стоимость подачи одного заказа, руб. Оптимальный размер заказа соответствует минимальной величине совокупных издержек. Исходя из этого, для расчета оптимального размера заказа используется формула Вилсона Формула Вилсона (Wilson) имеет вид: Q — оптимальный размер заказа, шт.; А — затраты на поставку единицы заказываемого продукта, pyб S— потребность в заказываемом продукте за определенный период, шт.; W— затраты на хранение единицы запаса, руб./шт. Используя формулу, определяем оптимальный размер заказа по имеющимся исходным данным: Округление оптимального размера заказа в большую сторону помогает избежать дефицита комплектующего изделия. Таким образом, оптимальный размер заказа составляет 95 шт. 4.1. Система с фиксированным размером заказа Задача 2 Рассчитать параметры системы управления запасами с фиксированным размером заказа для производственного предприятия. План годового выпуска продукции производственного предприятия составляет 800 единиц, при этом на каждую единицу готовой продукции требуется 2 единицы комплектующего изделия КИ-1. Известно, что стоимость подачи одного заказа составляет 200 руб., цена единицы комплектующего изделия — 480 руб., а стоимость содержания комплектующего изделия на складе составляет 15% его цены. Время поставки, указанное в договоре о поставке, составляет 10 дней, возможная задержка поставки — 2 дня. Число рабочих дней в году — 226 дней. Необходимо рассчитать параметры системы управления запасами с фиксированным размером заказа. Решение Основной параметр модели – размер заказа, который вычисляется описанным в предыдущей задаче способом. Таким образом, главный критерий оптимизации в такой модели - минимизация совокупных затрат на хранение запасов и размещение заказа (если мы заказываем продукцию редко, но большими партиями, возникают затраты, связанные с хранением и порчей продукции, если заказываем часто – возникают затраты связанные с транспортировкой маленьких партий, отсутствием оптовых скидок и т.д.). Методика расчета основных параметров модели приведена в табл. 4.1. Таблица 4.1 Порядок расчета параметров модели управления запасами с фиксированным размером заказа
Схематично модель управления запасами с фиксированным размером заказа изображена на рис. 4.2. 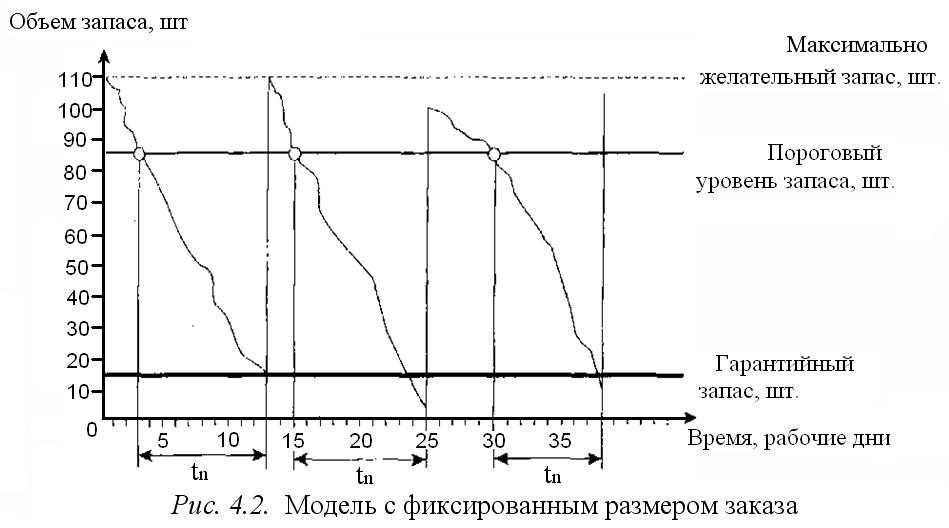 Рис. 4.2. Модель с фиксированным размером заказа tn – время поставки, о – точка заказа Результаты расчета основных параметров модели управления запасами с фиксированным размером заказа приведены в табл. 4.2. Таблица 4.2 Результаты расчета основных параметров модели
4.2. Система с фиксированным интервалом времени между заказами Задача 3 Рассчитать параметры системы управления запасами с фиксированным интервалом времени между заказами для производственного предприятия. План годового выпуска продукции производственного предприятия составляет 800 единиц, при этом на каждую единицу готовой продукции требуется 2 единицы комплектующего изделия КИ-1. Известно, что оптимальный размер заказа — 95 шт. Время поставки, указанное в договоре о поставке, составляет 10 дней, возможная задержка поставки — 2 дня. Число рабочих дней в году — 226 дней. Необходимо рассчитать параметры системы управления запасами с фиксированным интервалом времени между заказами. Решение В работе системы с фиксированным интервалом времени между заказами оптимальный размер заказа непосредственно не используется. Однако эффективный интервал времени между заказами, являющийся исходным параметром данной модели, предлагается исходя из оптимального размера заказа. Отношение величины потребности к оптимальному размеру заказа равно количеству заказов в заданный период, а число рабочих дней в заданном периоде, отнесенное к количеству заказов, равно интервалу между заказами, соответствующему оптимальному режиму работы системы. Следовательно, интервал времени между заказами можно рассчитать по следующей формуле: I — интервал времени между заказами, дн.; N— число рабочих дней в периоде, дн.; Q — оптимальный размер заказа, шт.; S— потребность, шт. Схематично модель управления запасами с фиксированным интервалом времени между заказами изображена на рис. 4.3.  Рис. 4.3. Модель с фиксированным интервалом времени между заказами tn – время поставки, о – точка заказа Методика расчета основных параметров модели приведена в табл. 4.3. Таблица 4.3 Расчет параметров модели управления запасами с фиксированным интервалом времени между заказами
Результаты расчета основных параметров модели управления запасами с фиксированным интервалом времени между заказами приведены в табл. 4.4. Таблица 4.4 Результаты расчета основных параметров модели
4.3.Определение оптимального размера заказа при наличии оптовой скидки (модель с дисконтированием по размеру партии поставки) Суть этой модели состоит в учете скидки (дисконта) с цены закупаемого ресурса при увеличении объема партии. В качестве исходной информации здесь дополнительно должна быть использована таблица дисконтирования, а в модель введен еще один параметр – цена ресурса. Алгоритм решения задачи представлен на рис.4.4. 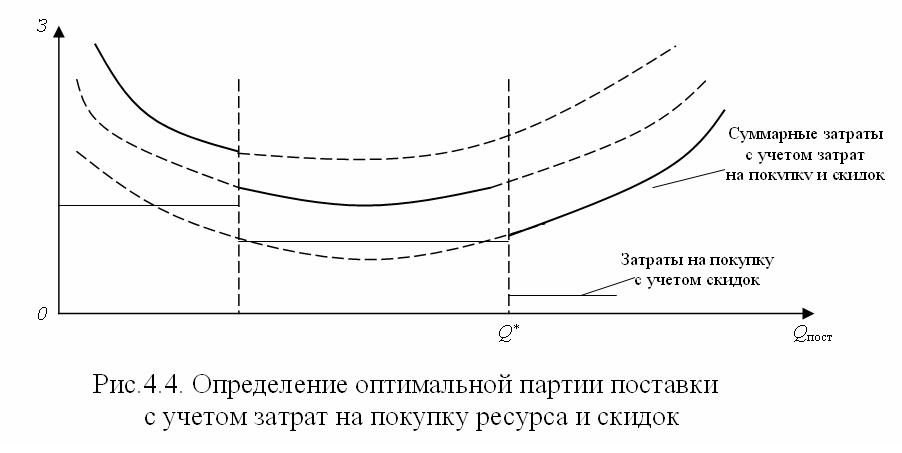 Рис. 4.4. Определение оптимальной партии поставки с учётом затрат на покупку ресурса и скидок Оптимальный размер партии поставки ресурса определяется отдельно для каждого интервала, где цена неизменна. Затем методом прямого перебора отыскивается лучший вариант, минимизирующий суммарные затраты на поставку, хранение и покупку ресурса с учетом скидки, действующей на интервале. Учитывая то, что цена в этой модели различна на разных интервалах, корректировка параметров модели позволит получить более точное решение задачи. Задача 4 Предприятие-поставщик установило следующие цены на свою продукцию – листовую пластмассу с учетом системы оптовых скидок: до 1000 листов – 180,0 руб/лист; от 1000 до 5000 листов – 175,0 руб/лист; 5000 листов и более – 172,5 руб/лист. Затраты на заказ у предприятия-потребителя пластмассы составляют 450 руб., текущие затраты на ее хранение – 36 руб/год за лист – практически не зависят от цены листа, годовая потребность – 10 000 листов. Требуется определить размер оптимальной партии закупки пластмассы с учетом скидок. Решение Начнем с классического расчета оптимальной партии поставки: Как видим, оптимальная партия попадает в первый ценовой интервал. Это значит, что меньшие суммарные затраты могут быть только на границах – в начале второго или третьего ценовых интервалов. Проверим эти точки, для чего рассчитаем в них суммарные затраты на заказ, приобретение и хранение пластмассы. Суммарные затраты составят:
2) при закупке по 1000 листов (нижняя граница второго интервала) 3) при закупке по 5000 листов (нижняя граница третьего интервала) Таким образом, при закупках пластмассы оптимальными партиями, расчет величины которой был выполнен обычным путем, затраты окажутся выше, чем при закупках партиями большого размера, ввиду того, что скидки оказывают существенное влияние на общую сумму затрат. Расчет показывает, что из двух граничных точек следует выбрать минимальный размер партии на втором интервале, т.е. Qпост = 1000 листов. |
