Логистика практикум. Учебное пособие практически задачи, примеры решения, варианты для самостоятельной работы, тесты Москва 2009 ббк 330 (075. 8) Д53
 Скачать 1.94 Mb.
|
|
Глава 7. Сервисная логистика В условиях «рынка покупателя», продавец организует свою деятельность, исходя из покупательского спроса. При этом спрос не ограничивается спросом на товар. Покупатель диктует свои условия также и на состав, и на качество услуг, оказываемых ему в процессе поставки товара. Задача 1 Имеются следующие данные об услугах, оказываемых фирмой. Перечень теоретически возможных услуг приведен в табл. 7.1. Таблица 7.1 Перечень услуг, которые теоретически могут быть оказаны фирмой
Номера услуг, фактически оказываемых фирмой: 7, 8, 11, 16, 21, 27, 32. Определите уровень сервиса. Решение Уровень сервиса рассчитывается по формуле 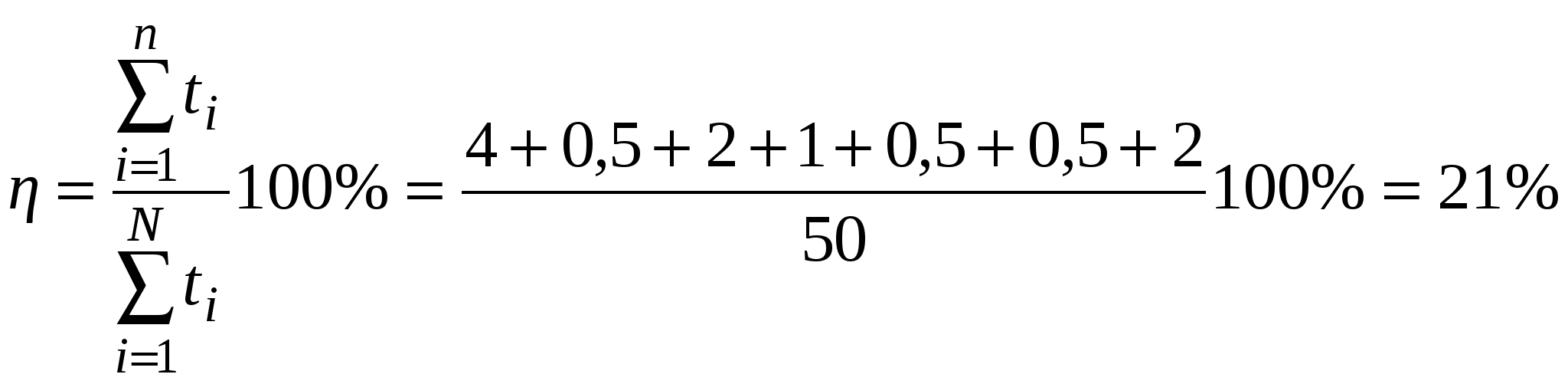 Тесты 1.Сервис — это: а)работа по оказанию услуг в процессе удовлетворения нужд; б)обслуживание потребителей; в)предоставление гарантий в процессе продажи товаров. 2.Что является объектом логистического сервиса: а)материальный поток; б)материальные и связанные с ними информационные поток в)потребители материального потока? 3.Кем может осуществляться логистический сервис: а) предприятием — изготовителем продукции; б)посредниками; в)любым участником распределительной цепи? 4.Логистический сервис бывает: а)предпродажным; б)послепродажным; в)во время продажи; г)все ответы верны; д)верны ответы (а) и (б); е)верны ответы (а) и (в); ж)верны ответы (б) и (в). 5.Как увеличиваются затраты на обслуживание при уменьшении уровня логистического обслуживания: а)увеличиваются; б)уменьшаются; в)практически не меняются? 6.Как меняются потери, вызванные ухудшением обслуживания при уменьшении уровня обслуживания: а)увеличиваются; б)уменьшаются; в)сначала увеличиваются затем уменьшаются; г)сначала уменьшаются затем увеличиваются? 7.Графически оптимальный уровень сервиса находится: а)в точке максимума кривой общих затрат и потерь; б)в точке минимума общих затрат и потерь; в)в точке, где касательная перпендикулярна оси X; г)не зависит от кривой общих затрат и потерь. ВЫВОДЫ ПО РАЗДЕЛУ В условиях «рынка покупателя» продавец вынужден строить свою деятельность исходя из покупательского спроса. При этом спрос не ограничивается спросом на товар. Покупатель диктует свои условия также и в области состава и качества услуг, оказываемых ему в процессе поставки товара. Работа по оказанию услуг, т.е. по удовлетворению чьих-либо нужд, называется сервисом. Природа логистической деятельности предполагает возможность оказания потребителю материального потока разнообразных логистических услуг. Логистический сервис неразрывно связан с процессом распределения и представляет собой комплекс услуг, оказываемых в процессе поставки товаров. Всю работу в области логистического обслуживания можно разделить на три основные группы: предпродажная; работа по оказанию логистических услуг, осуществляемая в процессе продажи товаров; послепродажный логистический сервис. Сервис оценивают показателем «уровень обслуживания», который определяется на основе потерь, вызванных ухудшением обслуживания и затрат на обслуживание. Глава 8. Информационная логистика В основе управления материальным потоком лежит обработка информации, циркулирующей в логистических информационных системах. В основе логистического анализа лежит применение логистической функции, с помощью которой описываются законы роста, присущего многим формам и уровням жизни, а также сфере материального производства и процессам насыщения потребительского спроса. Например, спроса на цветные телевизоры: сначала медленный, но все ускоряющийся рост доли семей, имеющих телевизор, переходящий в равномерный рост; затем рост доли семей, имеющих телевизор, замедляется по мере приближения этого показателя к 100%. График логистической функции имеет форму латинской буквы «S», положенной на бок. Поэтому его еще называют S-образ-ной кривой. Эта кривая имеет две точки перегиба и характеризуется переходом от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста к замедляющемуся (выпуклость). В целом логистический закон отражает динамику многих процессов в пространстве и во времени (например, зарождения нового организма или популяции, их отмирания, различных переходных состояний и т. п.). Логистической закономерности присуще свойство отражать изменения возрастающего ускорения процесса на замедляющееся или, наоборот, — при обратной форме кривой. Эта важная особенность дает возможность определить статистическим путем различные критические, оптимальные и другие практически ценные точки. В основе логистической функции лежит закономерность, выраженная уравнением Ферхюльста: 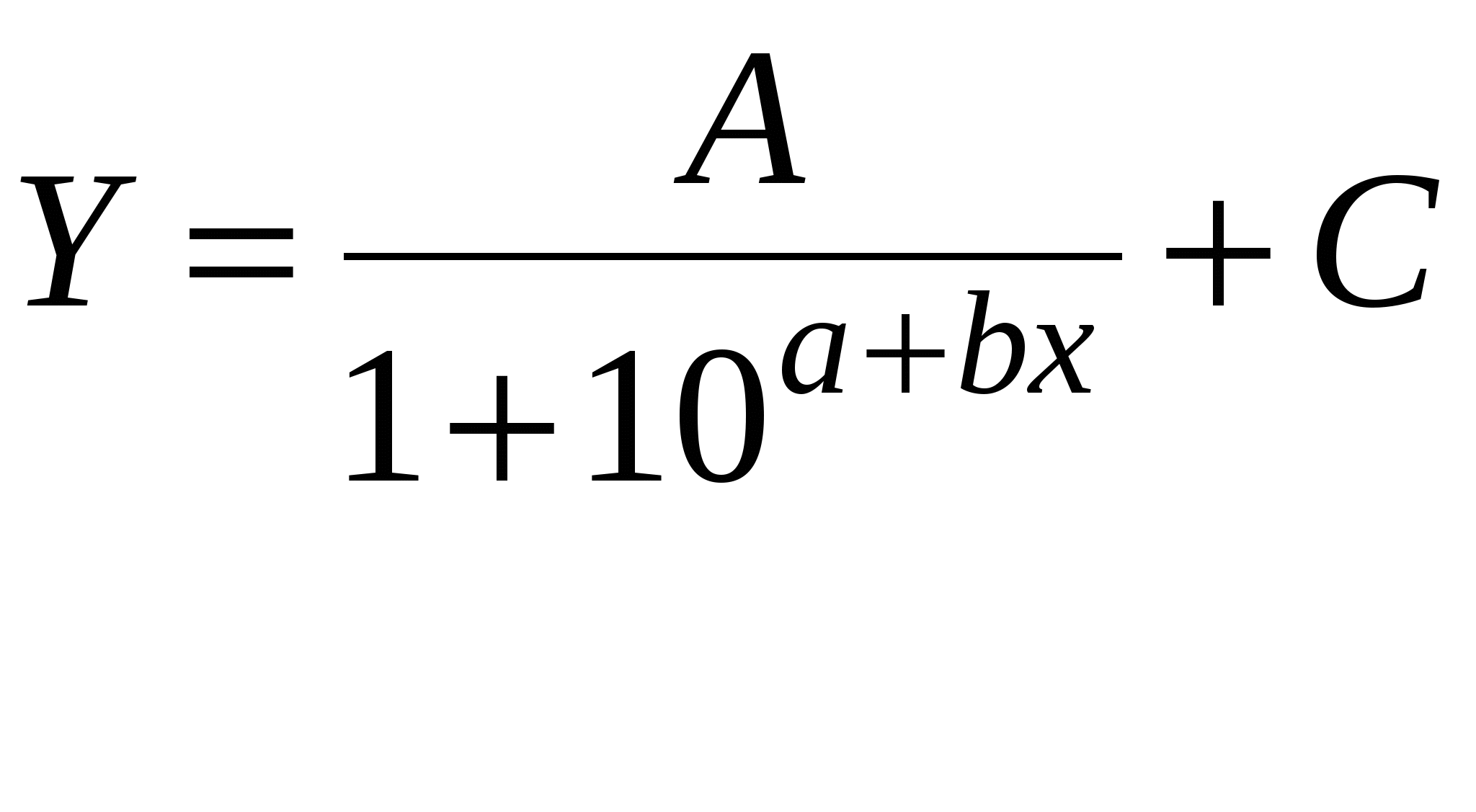 Y— значение функции; х— время; А — расстояние между верхней и нижней асимптотами; С — нижняя асимптота, т. е. предел, с которого начинается рост функции; a, b — параметры, определяющие наклон, изгиб и точки перегиба графика логистической функции (рис. 8.1). Для решения уравнения логистической функции первоначально надо определить верхнюю и нижнюю асимптоты. Это с достаточной точностью можно сделать по эмпирическому ряду путем простого его просмотра. Значение верхней асимптоты можно проверить аналитически по формуле: 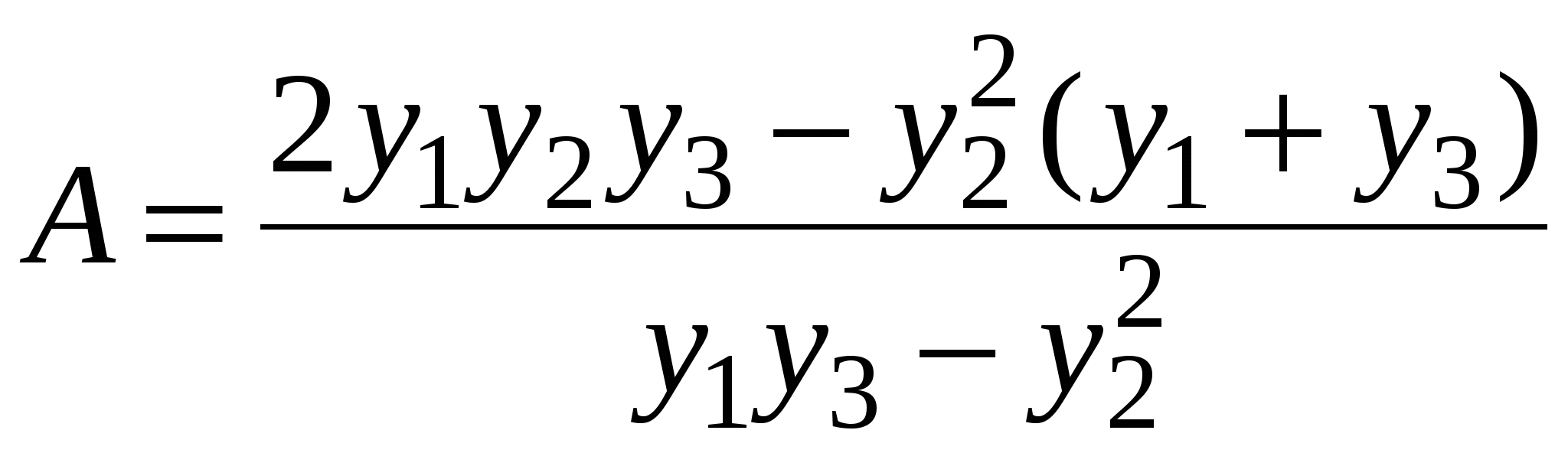 у1, у2,, у3 — три эмпирических значения функции, взятые через равные интервалы аргумента. 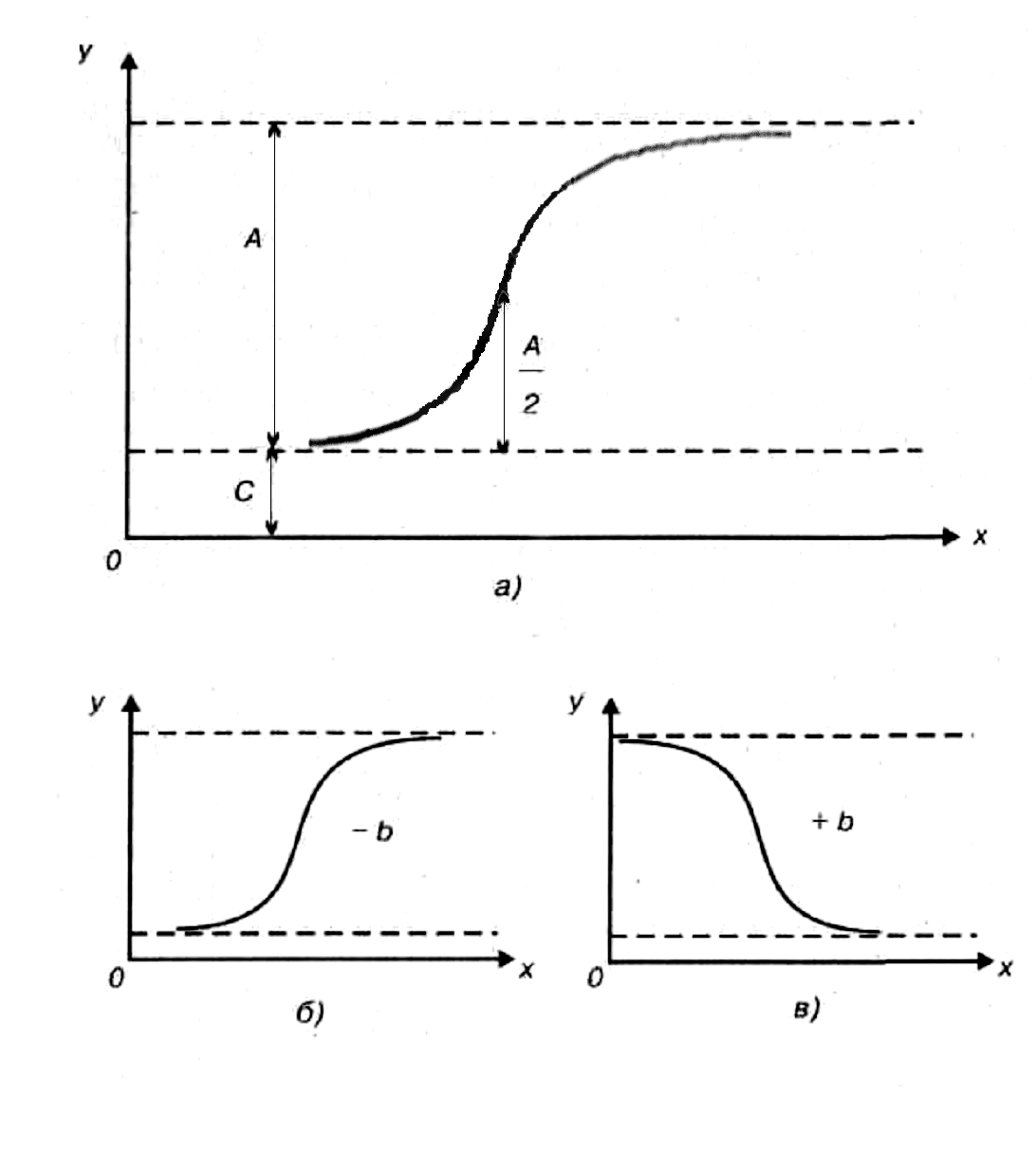 Рис 8.1. Графики логистических функций Затем уравнение логистической функции выражается в следующей логарифмической форме:  Обозначив левую часть этого уравнения через lg Z, получим параболу первого порядка: lg Z = а + bх Для определения параметров этого уравнения служит следующая система нормальных уравнений, решаемая методом наименьших квадратов: 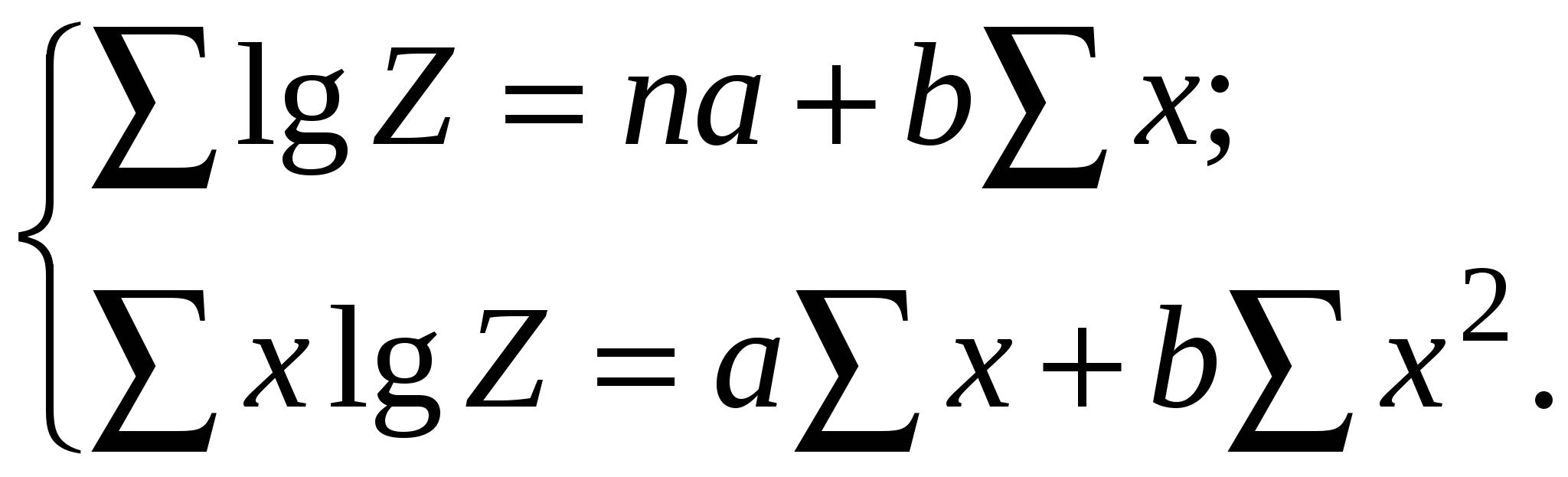 Если найти из этих уравнений параметры а и Ь, то можно составить ряд величин (а + Ьх), равных теоретическим значениям lg (А/(ух — С) - 1). Определяя величины (А/(ух - С) - 1), легко составить ряд теоретических значений функции ух. Если С.= 0, а верхняя асимптота = 100%, или 1, то уравнение логистической функции упрощается до формы:  Технику расчетов, связанных с практическим использованием уравнения логистической функции, легче освоить на конкретных примерах. Такие примеры известны в биометрии, при определении тенденций роста производства предметов потребления, в демографических расчетах и других процессах. Полученные результаты исследований логистической закономерности развития железнодорожного транспорта России и ряда других закономерностей свидетельствуют о важности теоретических обобщений, проведенных этим методом. Задача 1 В качестве примера логистического анализа рассмотрим определение логистической закономерности, описывающей конверсию автомобильной промышленности США на производство военной продукции во время второй мировой войны. Главными видами военной техники, выпускаемой автомобильной промышленностью США в период второй мировой войны, являлись: самолеты, авиадвигатели и их части, военные автомашины, танки и агрегаты к ним, судовое оборудование, пушки, боеприпасы и пр. Известны следующие данные об объеме производства военной продукции по годам (табл. 8.1). Таблица 8.1
Динамика объема производства военной продукции, выпускаемой автомобильной промышленностью США, представлена на рис. 8.2. По оси абсцисс – время (в годах), по оси ординат – выпуск (в млрд. долл.). На графике можно выделить следующие периоды: Период D—К. Наращивание выпуска военной продукции в течение 1941 г. обеспечивалось ростом производства «домобилизационной» продукции на военных заводах и было связано с переходом на трехсменную работу при 7-дневной рабочей неделе и с пуском законсервированных заводов-дублеров. Период K—L. В первую половину 1942 г. рост выпуска продукции автомобильными фирмами определялся главным образом конверсией гражданской промышленности на выпуск военной продукции. В течение второй половины 1942 г. конверсия продолжалась, но определяющую роль играли перестройка гражданской промышленности и новое строительство. Период L—M. Рост выпуска военной продукции в течение 1943 г. характеризовался перестройкой гражданской промышленности и вводом в строй вновь созданных объектов. 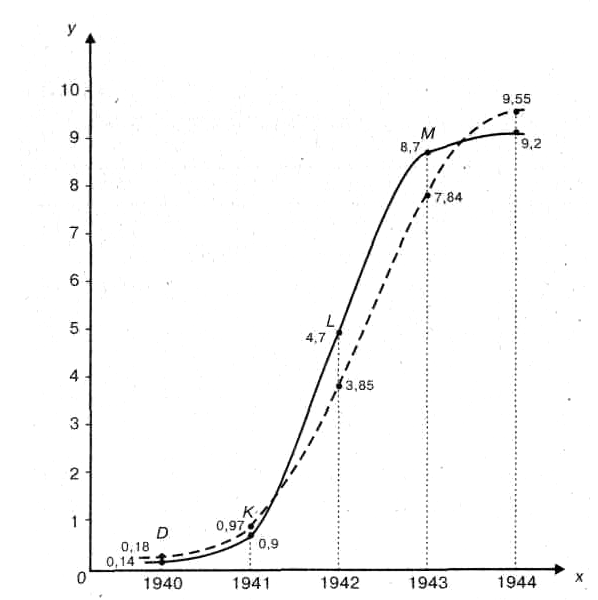 Рис. 8.2. Динамика обьёма производства военной продукции, выпускаемой автомобильной промышленностью США. Найдем уравнение этой закономерности, приняв А = 10, С = 0, n = 5. Для составления системы нормальных уравнений предварительно рассчитаем величины  (табл. 8.2).Таблица 8.2 Расчет данных для системы нормальных уравнений
По итогам таблицы составляем систему нормальных уравнений: 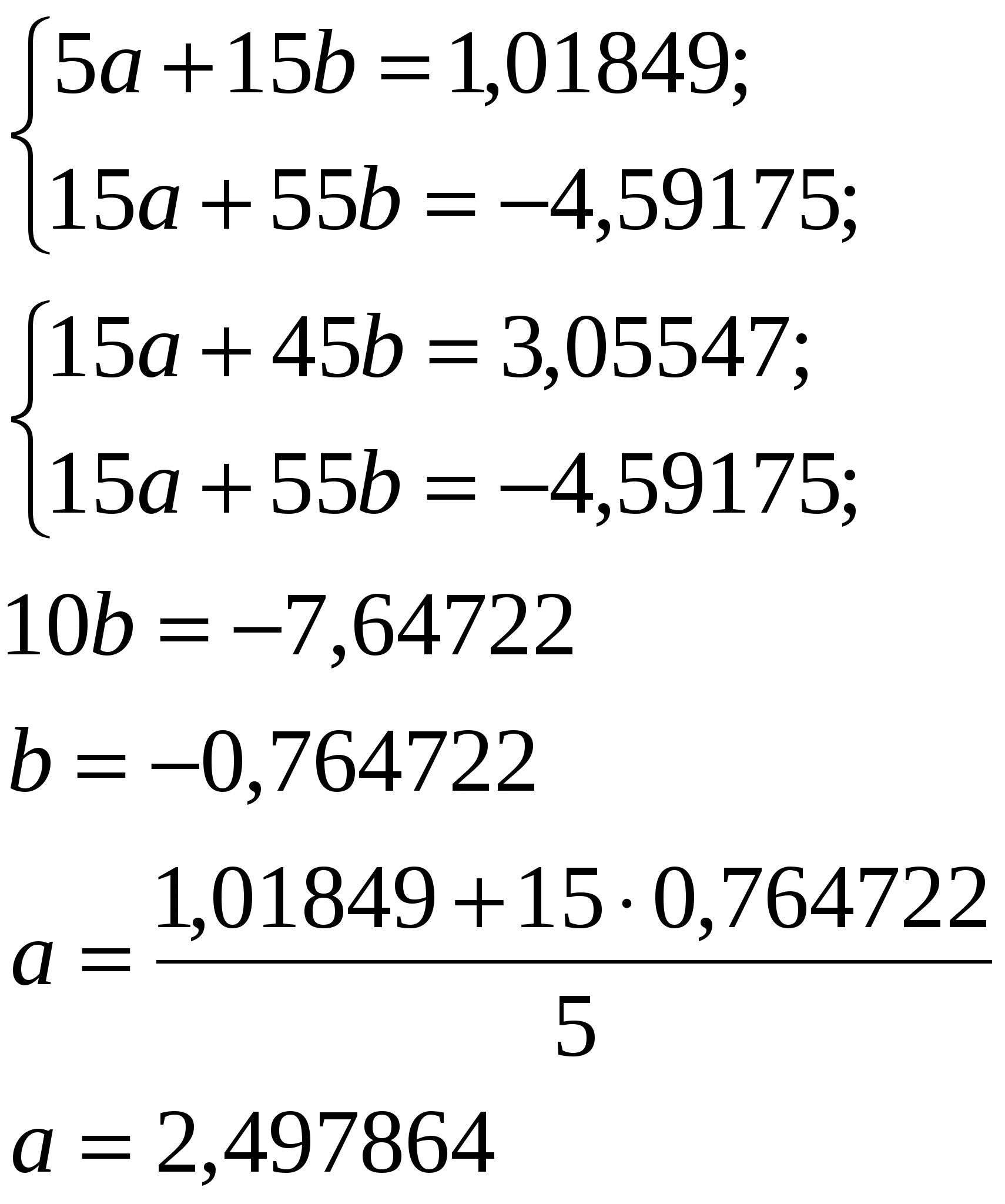 Подставляя в уравнение (1) вместо а и b их значения, а также величину А = 10, имеем:  По этому уравнению рассчитываем ожидаемые значения функции ух. Расчет показан в табл. 8.3. Таблица 8.3 Расчет значений 
Сравнивая вычисленные значения ( ) с эмпирическими (Y), видим, что они достаточно полно согласуются между собой. Более наглядно это представлено на рис. 3.1, где на фоне эмпирической кривой пунктиром изображена и кривая вычисленных значений ().Найдем точку перегиба — момент перехода возрастающей скорости в убывающую:  лет (в марте 1943 г.)Y = (A/2) + C = (10/2) + 0 = 5,0 млрд. долл. Точка пересечения с осью ординат имеет координаты:  (млрд. долл.) лет (в 1939 г.)Ошибка составляет:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
