Логистика практикум. Учебное пособие практически задачи, примеры решения, варианты для самостоятельной работы, тесты Москва 2009 ббк 330 (075. 8) Д53
 Скачать 1.94 Mb. Скачать 1.94 Mb.
|
|
Глава 6. Транспортная логистика Материальный поток на пути от первичного источника сырья (поставщика материальных ресурсов) до конечного потребителя готовой продукции проходит ряд этапов. Первый – это от поставщика сырья и материалов до предприятия с помощью различных видов транспорта. Второй этап – движение потока внутри предприятия по стадиям производственного процесса; осуществляется в ходе выполнения технологических операций. Третий этап – это движение материального потока от предприятия-изготовителя до конечного потребителя продукции. 6.1. Выбор поставщика товара Задача 1 В Вашу консультационную фирму обратилась голландская компания с вопросом: где ей выгоднее закупать комплектующие: в Европе или в Юго-Восточной Азии? Исходные данные:
Дайте ответ голландской компании. Решение Сначала рассчитаем долю дополнительных затрат, возникающих при доставке из Юго-Восточной Азии, в удельной стоимости поставляемого груза по следующей формуле: Тт — транспортный тариф (долл. США/куб, м); У — удельная стоимость поставляемого груза (долл. США/куб, м); Пи — импортная пошлина на товар из Юго-Восточной Азии (%); Зп — ставка на запасы в пути (%); Зс — ставка на страховые запасы (%). Подставив в формулу (5) исходные данные, получаем: Теперь определим разницу между стоимостью товаров в Европе и в Юго-Восточной Азии, приняв стоимость в Юго-Восточной Азии за 100%: Се — стоимость товара в Европе (долл. США), Са — стоимость товара в Юго-Восточной Азии (долл. США). Подставив в формулу (6) исходные данные, получаем: Так как Рс больше Д, то голландской компании выгоднее закупать комплектующие в Юго-Восточной Азии. 6.2. Выбор вида тары для транспортировки продукции Задача 2 Продукция транспортируется в стандартных контейнерах в ящиках или на поддонах. Если используются поддоны, то в контейнер вмещается 300 изделий (25 поддонов в одном контейнере, 12 изделий на одном поддоне). Если штабелируются ящики, то в контейнер вмещается 480 изделий (40 ящиков в одном контейнере, 12 изделий в одном ящике). Транспортные расходы в расчете на один контейнер:
—при транспортировке на 1000—1999 км — 2000 у.е., —при транспортировке на 2000 и более км — 3000 у.е. Почасовая ставка погрузочно-разгрузочных работ (ПРР): —вручную—36 у.е., —вилочным погрузчиком — 54 у.е. Затраты рабочего времени на погрузку:
Необходимо определить затраты на один поддон и один ящик при транспортировке продукции на каждое из указанных расстояний, на основе расчетов выбрать наиболее рациональный вид тaры. Решение Стоимость транспортировки одного поддона или ящика определяется в зависимости от стоимости транспортировки контейнера и количества поддонов или ящиков в одном контейнере, а также в зависимости от расстояния перевозки. Результаты расчетов стоимости транспортировки одного поддона и одного ящика сведем в табл. 6.1. Таблица 6.1
Стоимость погрузки одного поддона и одного ящика определяем в зависимости от затрат времени на погрузку и почасовой ставки ПРР (табл. 6.2.) Таблица 6.2
Общие затраты на транспортировку одного поддона и одного ящика включают затраты на перевозку и затраты на погрузку одного поддона и одного ящика. Результаты расчетов приведены в табл. 6.3. Таблица 6.3.
Как видно из табл. 6.3, несмотря на то, что почасовая ставка ручной погрузки тары меньше, чем почасовая ставка работы вилочного погрузчика, стоимость погрузки одного поддона или ящика вручную дороже, чем стоимость погрузки вилочным погрузчиком, так как время погрузки одного поддона или ящика вручную в два раза больше, чем время погрузки вилочным погрузчиком. В итоге получается, что суммарные затраты на транспортировку одного поддона (ящика) при .погрузке вилочным погрузчиком будут меньше, чем при погрузке вручную. Погрузка одного ящика вручную и механическим способом будет дешевле погрузки одного поддона. Следовательно, суммарные затраты на один ящик будут меньше, чем на один поддон. Таким образом, ящики являются наиболее предпочтительным видом тары, при этом загружать их в контейнер дешевле вилочным погрузчиком. 6.3. Пример решения транспортной задачи венгерским методом Задача 3 Найти оптимальный вариант назначений, если матрица производительности имеет следующий вид: 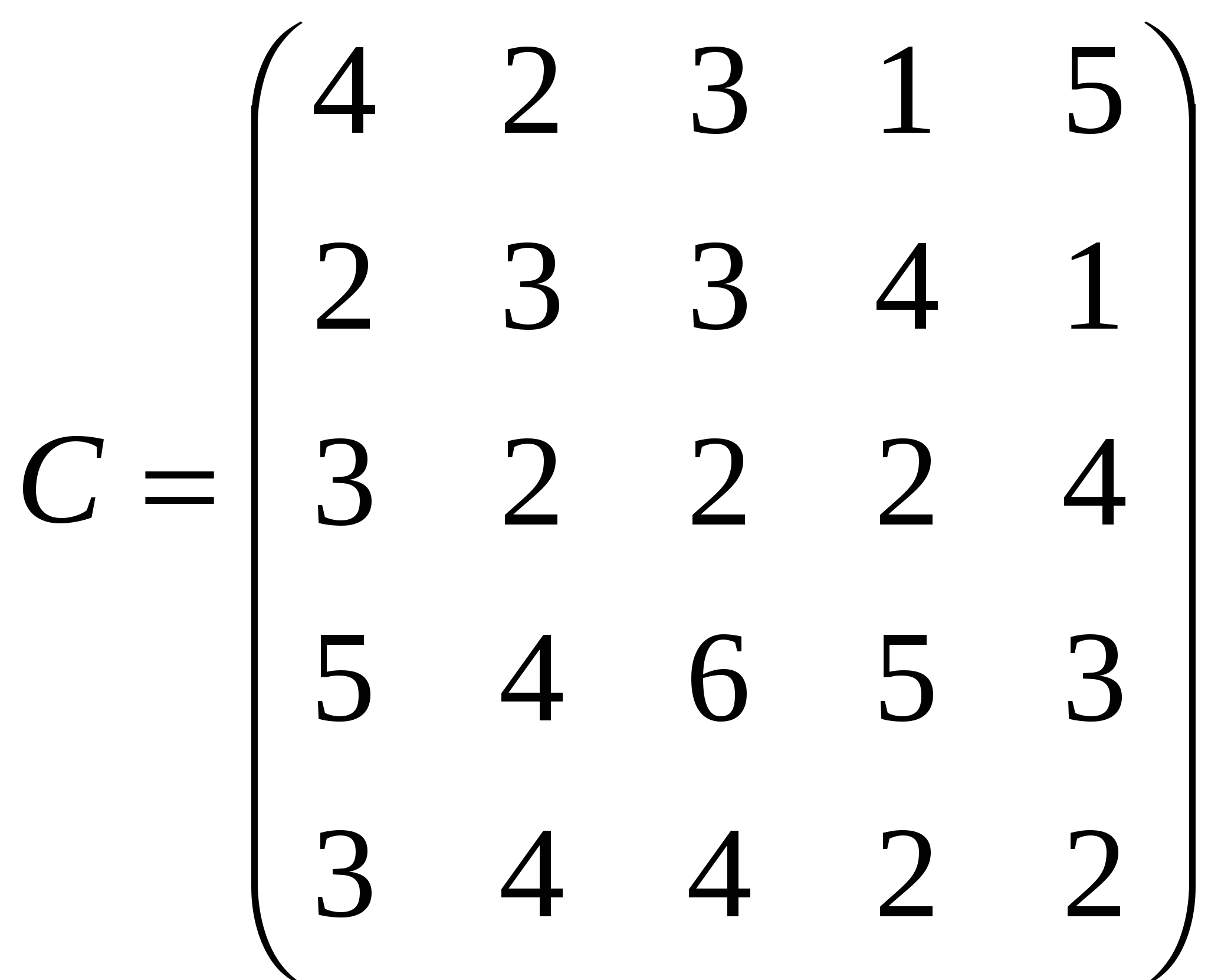 Ниже приводится цепочка матриц, получаемых в процессе решения задачи, с соответствующими пометками. Снятие знака выделения «+» отмечено заключением его в рамку. Цепочка на этапе 2 отмечается стрелками. 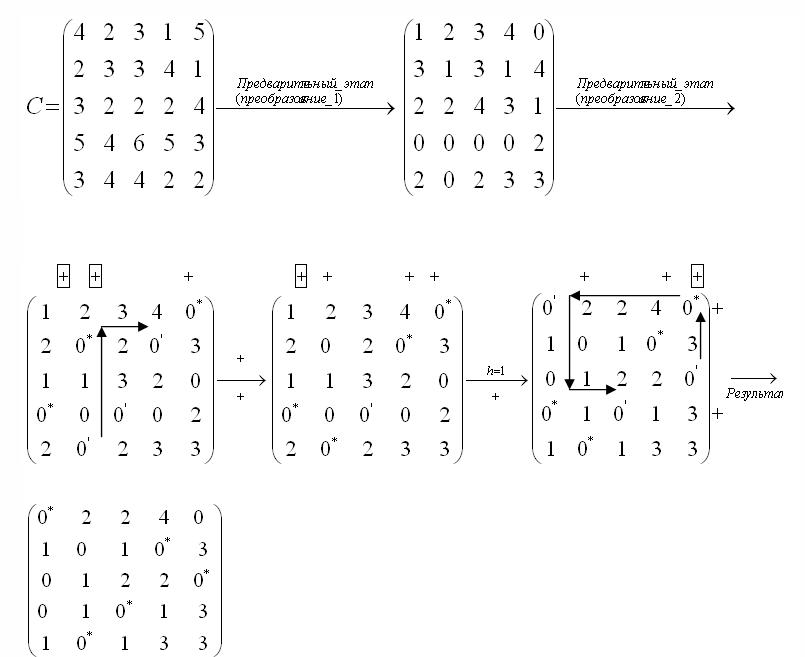 Оптимальный вариант назначений х11 = х24= х35 = х43 = х52= 1, остальные Хij= 0, т. е. первый исполнитель назначается на первую работу, второй — на четвертую, третий — на пятую, четвертый — на третью, пятый — на вторую. Соответствующая ему суммарная производительность 4 + 4 + 4 + 6 + 4 = 22. Пояснения к решению задачи. Процесс нахождения оптимального варианта назначений состоит из предварительного этапа и двух итераций. Предварительный этап На этом этапе осуществляются два последовательных преобразования матрицы С. Сначала находится максимальный элемент в каждом столбце: в первом столбце максимальный элемент равен 5, во втором — 4, в третьем — 6, в четвертом — 5, в пятом — 5. Из максимального элемента вычитаются элементы этого столбца. Получается неотрицательная матрица, в каждом столбце которой есть хотя бы один нуль. Затем из каждой строки полученной матрицы вычитаем минимальный элемент этой строки. В результате подготовительного этапа Осуществлен переход к неотрицательной матрице, в каждом столбце и каждой строке которой имеется хотя бы один нуль. В первом столбце матрицы отмечаем звездочкой нуль, расположенный в четвертой строке, во втором столбце — нуль во второй строке. В третьем столбце единственный нуль находится в четвертой строке, в которой уже имеется 0*, поэтому нуль в третьем столбце звездочкой не отмечается. Аналогично не отмечаются звездочкой нули в четвертом столбце, так как они находятся во второй и четвертой строках, где уже имеются выделенные нули. В пятом столбце отмечаем звездочкой нуль в первой строке. В результате получается три независимых нуля, следовательно, для решения задачи необходимо проведение двух итераций. Итерация 1 Этап 1 Выделяем знаком «+» первый, второй и пятый столбцы матрицы, содержащие нули со звездочкой. Просматриваем невыделенные нули матрицы, начиная с третьего столбца. Отмечаем штрихом нуль этого столбца, расположенный в четвертой строке. Поскольку в этой строке имеется 0*, то строка подлежит выделению (ставим знак «+» справа, от четвертой строки). Одновременно уничтожается (обводится рамкой) знак выделения над первым столбцом, содержащим 0* в четвертой строке (случай (а)). Далее, отмечаем штрихом нуль, расположенный в четвертом столбце и во второй строке. Поскольку во второй строке имеется О* во втором столбце, то выделяем вторую строку и снимаем знак выделения над вторым столбцом. Так как во втором столбце имеются невыделенные нули, отмечаем нуль этого столбца, расположенный в пятой строке. Пятая строка матрицы не содержит О*. Следовательно, имеет место случай (б) (исход IA), т. е. необходим переход к этапу 2. Этап 2 Строим цепочку. От последнего нуля со штрихом (пятая строка, второй столбец) движемся по столбцу к нулю со звездочкой (второй столбец, вторая строка), затем от 0* — к 0', расположенному в этой же строке в четвертом столбце. Поскольку в четвертом столбце матрицы нет 0*, процесс образования цепочки закончен. Искомая цепочка состоит из элементов: 0'52, 0*22, 0'24. Для завершения этапа 2, а вместе с ним и первой итерации, необходимо поставить звездочки над нулями цепочки, отмеченными штрихами, уничтожить звездочку над единственным четным элементом цепочки и стереть все знаки выделения. В результате итерации / число независимых нулей увеличилось на единицу и стало равно 4. Итерация 2 Этап 1 Выделяем столбцы, содержащие нули со звездочкой: первый, второй, четвертый и пятый. Единственный нуль в невыделенном (третьем) столбце расположен в четвертой строке, в которой имеется.0*. Следовательно, выделяем четвертую строку и уничтожаем знак выделения над первым столбцом (случай (а)). После этого все нулевые элементы матрицы оказываются выделенными (исход IB), поэтому завершаем этап 1 и переходим к этапу 3. Этап 2 Минимальным из числа невыделенных элементов матрицы является единица. Поэтому из всех элементов невыделенных строк (первой, второй, третьей, пятой) вычитаем h= 1, а к элементам выделенных столбцов (второго, четвертого, пятого) прибавляем h= 1. Получается матрица, эквивалентная предыдущей и содержащая незанятые нули. Переносим все знаки выделения (+,*,') с предыдущей матрицы, кроме знаков, обведенных рамкой, и переходим к этапу 1. Этап 3 Отмечаем штрихом невыделенный нуль первого столбца первой строки, так как в первой строке имеется 0* в пятом столбце, выделяем первую строку и снимаем знак выделения над пятым столбцом. В пятом столбце имеется невыделенный нуль, расположенный в третьей строке, отмечаем его штрихом. Поскольку в третьей строке нет нулей со звездочкой (случай (б)), переходим к этапу 2. Этап 4 Строим цепочку. От последнего 0' (третья строка, пятый столбец) движемся по столбцу до 0*, расположенного на пересечении первой строки и пятого столбца, далее от 0* — к 0', находящемуся в этой же строке в первом столбце, затем по первому столбцу к 0* (четвертая строка, первый столбец) и по строке 4 к 0', расположенному в третьем столбце. Так как в третьем столбце нет 0*, процесс образования цепочки закончен. Искомая цепочка состоит из элементов: 0'35, 0*15, 0'11, 0*4], 0'43. Снимаем звездочки у нулей из цепочки и заменяем звездочками штрихи у нулей из цепочки. В результате второй итерации число независимых нулей увеличилось на единицу и стало равно 5, поэтому процесс решения задачи закончен. 6.4. Решение транспортной задачи методом «северо-западного угла» Транспортная задача может быть формализовано описана следующим образом. Имеется тпоставщиков определенного вида продукции (либо т— количество мест, складов, откуда происходит поставка продукции). Максимальные объемы возможных поставок заданы и равны соответственно ai, ,i=1, 2,..., т. Эта продукция используется п потребителями. Объемы потребностей заданы и равны соответственно bj , j= 1, 2,..., п. Стоимость перевозки единицы продукции от i-го поставщика к j-му потребителю известна для всех i,jи равна Cij,. Установите такие объемы перевозокXijот каждого поставщика к каждому потребителю, чтобы суммарные затраты на перевозки были минимальными и потребности всех потребителей были удовлетворены (если только общий объем возможных поставок покрывает общий объем потребностей). Задача 4 На двух складах (А и В) имеется соответственно 50 и 40 т продукции. Таблица 6.4.1 Исходные данные для решения транспортной задачи 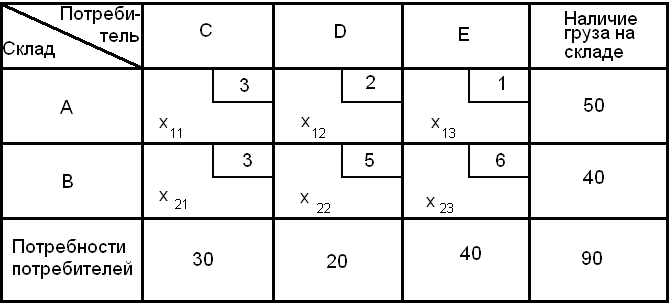 Стоимость перевозки от складов к потребителям приведена в табл. 1 (в правом верхнем углу каждой клетки). Например, стоимость перевозки единицы (1т) груза со склада А потребителю С равна 3 у.е. Спланируйте перевозки к трем потребителям (С, Dи Е) так, чтобы потребитель С получил 30 т груза, потребитель D— 20 т, потребитель Е — 40 т, а затраты на перевозку были минимальными. Для решения задачи на первом этапе составляется система ограничений и целевая функция. Система ограничений в общем виде (для нашей задачи) имеет вид 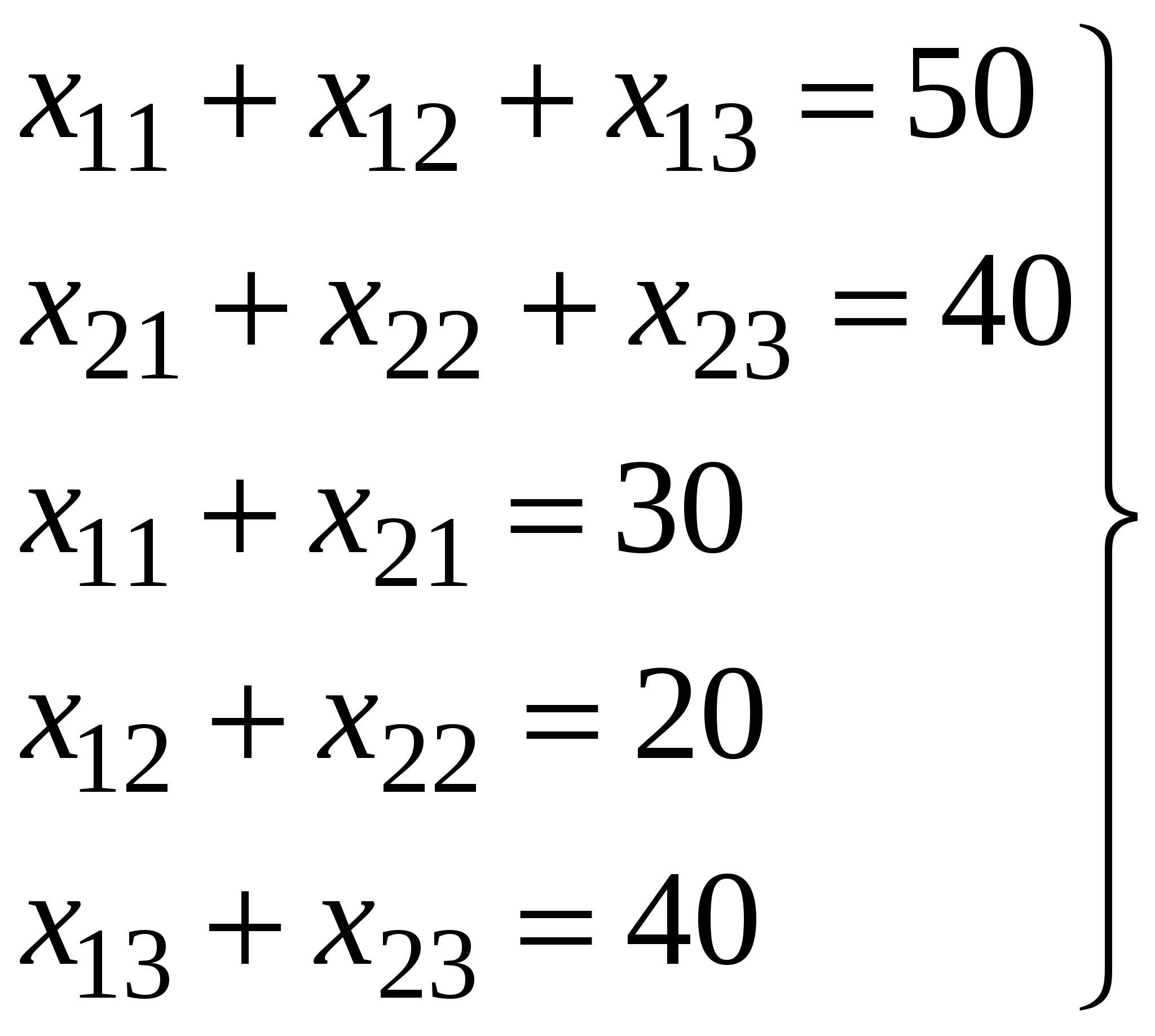 причем Хij > 0 для i = 1, 2; j = 1, 2, 3. Целевая функция затрат на перевозку, значение которой необходимо минимизировать при имеющихся ограничениях, выглядит следующим образом: Далее перераспределяются объемы поставок методом “северо-западного угла”, т.е. первой заполняется верхняя левая (северо-западная) клетка исходной таблицы. Примем объем перевозки со склада А кпотребителю С максимально возможным из условий задачи и равным 30 т. Потребитель С полностью удовлетворил свою потребность, и поэтому графу «С» в табл. 1 можно исключить из дальнейшего рассмотрения. В таблице 1 найдем «северо-западный угол» (теперь это клетка AD) и укажем максимально возможное значение. Оно рассчитывается следующим образом: со склада А уже перевезено 30 т груза, поэтому остаток на этом складе составляет 20 т (50—30). Вносим в клетку ADвместо X12значение, равное 20 т. Таким образом, весь груз со склада А перевезен потребителям и первая строка табл. 1 исключается из дальнейшего рассмотрения. Потребитель Dполностью удовлетворил свою потребность в грузе, и графу Dможно исключить из дальнейшего рассмотрения. В оставшейся части табл. 1 найдем новый «северо-западный угол» (клетка BE) и укажем в нем максимально возможное значение (40 т). В результате (в табл. 2) получено следующее распределение поставок: x11= 30;x12 = 20; x23 = 40. Таблица 6.4.2 Распределение поставок 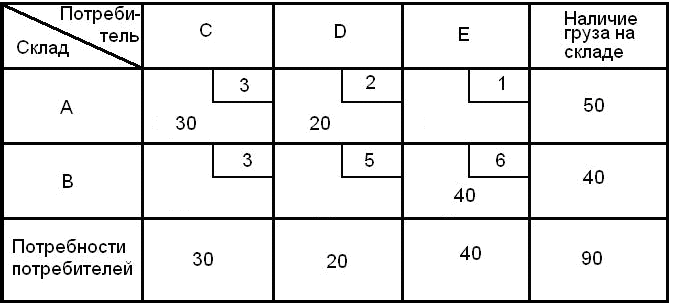 Значение целевой функции будет иметь вид В результате дальнейших вычислений мы получим оптимальное минимальное значение целевой функции. Расчеты громоздки, но легко реализуются с использованием компьютерных программ. Задания для самостоятельной работы Задача 1 В Вашу консультационную фирму обратилась голландская компания с вопросом: где ей выгоднее закупать комплектующие: в Европе или в Юго-Восточной Азии? Исходные данные:
Дайте ответ голландской компании. Задача 2 В Вашу консультационную фирму обратилась голландская компания с вопросом: где ей выгоднее закупать комплектующие: в Европе или в Юго-Восточной Азии? Исходные данные: •удельная стоимость поставляемого груза — 5000 долл. США/куб. м;
Дайте ответ голландской компании. Задача 3 Имеются три склада готовой продукции и четыре потребителя. На складах находятся 10, 20 и 15 т продукции. Потребители готовы купить 15, 12, 11 и 7 т этой продукции. Затраты на доставку 1 т продукции со склада 1 потребителям равны соответственно: 45, 15, 26 и 38 у.е.; со склада 2: 19, 25, 65 и 34 у.е.; со склада 3: 20, 24, 18 и 22 у.е. Сделайте первое распределение методом «северо-западного угла», найдите первое (возможно, неоптимальное) решение. Задача 4 Произвести расчет стоимости перевозки холодильных компрессоров из России на Кубу по двум вариантам: в контейнерах и в ящичной чаре. На основе расчетов выбрать наиболее экономичный вариант. Объем груза — 300 т. Схема перевозки: по железной дороге от Ростова до Санкт-Петербурга и далее морем от Санкт-Петербурга до Гаваны. Стоимость перевозки по железной дороге: в контейнерах — 13 200 долл. за 20-тонный контейнер; в ящичной таре — 36 900 долл./вагон. Загрузка груза: в контейнер — 5 т: в вагон — 13 т. Стоимость перевалки с железной дороги в морское судно: в контейнерах — 1500 долл./контейнер; в ящичной таре — 1210 долл./т.; Стоимость фрахта: в контейнерах — 2000 долл./ т; в ящичной таре — 2300 долл./т. Тесты 1.От какого фактора зависит время выполнения заказа потребителя: а)от срока доставки продукции транспортом; б)от количества посредников; в)от размера партии поставки? 2.Длительное время прохождения заказа: а)уменьшает количество запасов на предприятии; б)увеличивает уровень запасов на предприятии; в)не влияет на объем запасов.
а)скорость доставки груза и грузоподъемность транспортного средства; б)стоимость перевозки и скорость доставки груза; в)надежность соблюдения графика доставки и стоимости перевозки.
а)плату за перевозку грузов и пассажиров; б)сборы за дополнительные операции, связанные с перевозкой грузов и пассажиров; в)правила исчисления плат и сборов; г)все ответы верны; д)верны ответы (а) и (б). 9.Транспортный тариф — это... 10.Какая группа факторов, влияющих на размер транспортного тарифа, является общей для всех видов транспорта: а)грузоподъемность транспортного средства, расстояние перевозки, район; б)расстояние перевозки, тип транспортного средства, объемный вес груза; в)расстояние перевозки и масса груза? ВЫВОДЫ ПО РАЗДЕЛУ Материальный поток на пути от первичного источника сырья до конечного потребителя проходит ряд этапов: движение материального потока от источника сырья до предприятия; прохождение материального потока внутри предприятия по стадиям производственного процесса; движение материального потока от предприятия-изготовителя до конечного потребителя продукции. На всех этапах движение обеспечивается различными видами транспорта. Затраты на выполнение операций по транспортировке материальных потоков и погрузочно-разгрузочные операции составляют до 50% от суммы общих затрат на логистику. Выбор транспортного средства для доставки сырья или продукции зависит от стратегии предприятия. Учитываются: размещение производства, источники сырья и потребители; технико-экономические особенности различных видов транспорта; оптимальный уровень запасов; вид упаковки. Основными критериями выбора вида транспорта являются стоимость и скорость доставки продукции, зависящие от технико-эксплуатационных характеристик транспорта. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
