|
|
Цилиндр. Урок 106. Деление отрезка на 2, 4, 8 равных частей с помощью циркуля и линейки
Организационная структура урока
Этап урока
|
Содержание деятельности учителя
|
Содержание деятельности обучающегося
(осуществляемые действия)
|
Формируемые
способы
деятельности
обучающегося
|
II. Актуализация опорных знаний.
Устный счет.
Интеллектуальная разминка
|
Организует устный счет с целью актуализации знаний.
– Выполните задание на смекалку.
а) Расположите 10 точек на 5 отрезках так, чтобы на каждом отрезке было 4 точки.
б) Как записать число 100 шестью цифрами 4?
в) Как записать число 100 семью цифрами 4?
|
Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.
Решение:
а) 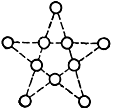
б) 100 = (444 – 44) : 4.
в) 100 = (4 · 4 + 4) · (4 · 4 + 4) : 4.
|
Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой.
Принимать и сохранять учебную цель и задачу.
Дополнять, уточнять высказанные мнения по существу полученного задания
|
|
– Вставьте пропущенные числа в «окошки»:
237 = 200 +  + 7 + 7
5629 =  + 600 + + 600 +  + + 
8934 =  + +  + +  + 4 + 4
12395 =  + 2000 + + 2000 +  + 90 + + 90 + 
34897 =  + 4000 + 800 + + 4000 + 800 +  + + 
126237 =  + +  + + + 200 + + 200 +  + 7 + 7
|
Запись:
237 = 200 + 30 + 7
5629 = 5000 + 600 + 20 + 9
8934 = 8000 + 900 + 30 + 4
12395 = 10000 + 2000 + 300 + 90 + 5
34897 = 30000 + 4000 + 800 + 90 + 7
126237 = 100000 + 20000 + 6000 + 200 + 30 + 7
|
III. Повторение по теме урока
|
Организует работу по закреплению знаний, обеспечивает контроль за выполнением задания.
– Сейчас я буду читать интересные факты. Используя многозначные числа, вы должны записать в тетрадь все, которые состоят более чем из трех разрядов единиц.
– Когда мы смотрим на самую дальнюю из видимых звезд, мы смотрим на 4 миллиарда лет в прошлое. Свет от нее, путешествующий со скоростью почти в 300 000 км/секунду достигает нас только через много лет.
– Автомобилю, движущемуся со средней скоростью 60 миль в час, потребовалось бы примерно 48 миллионов лет, чтобы достичь ближайшей к нам звезды (после Солнца) Проксимы Центавра.
– На борту станции «Мир» находится более 14 000 кг различной исследовательской аппаратуры.
– Общая масса станции «Мир» с двумя пристыковаными кораблями составляет более 36 000 кг.
– Если наполнить чайную ложку веществом, из которого состоят нейтронные звезды, то ее вес будет равняться примерно 110 миллионам тонн.
– Самый большой лунный кратер, видимый с Земли, называется Бэйли или «поле гибели». Он имеет площадь примерно в 26 000 квадратных миль.
– Первые карты Луны изготовил в 1609 году Томас Харриот.
– Самая высокая гора на Луне имеет высоту 11 500 метров.
– Горы на Марсе достигают высоты 25 000 м.
– Каждый день на Землю из космоса падает около 210 тысяч метеоритов. Правда, все они настолько малы, что сгорают в атмосфере.
– Если протянуть паутину до ближайшей к нам звезды в созвездии Центавра, то она весила бы 500 000 тонн.
– Около 27 тонн космической пыли падает на Землю каждый день. За год более 10 000 тонн пыли приземляется на Землю.
– Площадь солнечной поверхности размером с почтовую марку светит с такой же энергией, как и 1 500 000 свечей.
– Ганимед, самый большой из спутников планеты Юпитер, по своим размерам превосходит планету Меркурий. Диаметр
Ганимеда составляет примерно 5269 километров.
– Диаметр Луны – 3476 километров.
– Назовите самое большое число.
– Назовите самое маленькое число.
– Сколько единиц 1-го класса в самом маленьком числе?
– Сколько единиц 2-го класса в самом маленьком числе?
|
Выполняют задания, отвечают на вопросы, высказывают свое мнение.
Записывают многозначные числа.
– Самое большое число – 4 000 000 000.
– Самое маленькое число – 1 609.
– 609 единиц 1-го класса в самом маленьком числе.
– 1 единица 2-го класса в самом маленьком числе
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей.
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор.
Применять правила делового сотрудничества. Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Осуществлять контроль по результату
|
IV. Самостоятельная работа
|
Организует работу в группах по карточкам.
– Найдите сумму самого большого и самого маленького числа.
|
Работают в группах.
Ответ:
|
Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием
|
|
– Найдите разность 2 чисел: уменьшаемое содержит 11 единиц 2-го класса, а вычитаемое число содержит 5 единиц 2-го класса.
|
Ответ: 11500 – 5269 = 6231
|
|
– Увеличьте число, в котором 4 единицы тысяч, 1 сотня, 4 десятка, 7 единиц в 100 раз.
|
Ответ: 4147 · 100 = 414700.
|
|
– Уменьшите, число, в котором 36 тыс. единиц
(36.000), в 10 раз.
|
Ответ: 36000 : 10 = 3600.
|
|
– Уменьшите число, которое на 1 больше, чем 4149, на 100.
|
Ответ: 4150 – 100 = 4050
|
|
– Увеличьте число, которое составляет половину миллиона (500000) на 1000
|
Ответ: 500000 + 1000 = 501000
|
V. Итог урока. Рефлексия
|
Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися.
Проводит беседу по вопросам:
– Что нового узнали на уроке?
– Какими знаниями, полученными на уроке, вы хотели бы поделиться дома?
– Какое задание понравилось больше всего?
– Что вызвало затруднение?
– Понравилась ли вам работа на уроке? Оцените себя
|
Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию
|
Способность
к самооценке на основе критерия успешности учебной деятельности
|
Урок 135. Педагогическая диагностика № 3
Тип урока: решение учебной задачи, контроль знаний
|
Педагогические задачи: создать условия для проверки знаний по математике за курс начальной школы
|
Планируемые результаты
|
Предметные:
научатся применять полученные знания при выполнении заданий
|
Метапредметные:
Познавательные: овладевают умением подводить под понятия, выводить следствия; устанавливают причинно-следственные связи; строят логическую цепь рассуждений; используют доказательство.
Регулятивные: умеют работать по предложенному учителем плану
|
Личностные: расширяют познавательные интересы и учебные мотивы; умеют устанавливать, с какими учебными задачами могут справиться самостоятельно
|
Организационная структура урока
Этап урока
|
Содержание деятельности учителя
|
Содержание деятельности
обучающегося
(осуществляемые действия)
|
Формируемые
способы
деятельности
обучающегося
|
I. Диагностическая работа.
Вариант 1
|
Знакомит с содержанием диагностической работы, комментирует задания.
1. Как записать цифрами число двести тысяч сорок восемь?
1) 20 048; 2) 2 000 048; 3) 200 048; 4) 2 048.
2. Найди значение суммы чисел 3589 и 10645.
3. Найди значение разности чисел 4092 и 2368.
4. Найди значение частного чисел 8276 и 4.
1) 269; 2) 2069; 3) 2079; 4) 20069.
5. На мосту расположен знак, указывающий, что по мосту можно провезти груз весом не более 2 т 300 кг. Выбери вес груза, который можно провезти по этому мосту:
1) 2220 кг; 2) 3200 кг; 3) 2 т 301 кг; 4) 3 т.
6. Найди значение выражения:
720 : 90 + 13 ∙ 4 + 219.
1) 247; 2) 191; 3) 415; 4) 279.
7. В комнату с площадью пола 20 м2 постелили квадратный коврик со стороной 2 метра. Какая площадь комнаты осталась не занятой ковром?
1) 16 м; 2) 44 м2; 3) 16 м2; 4) 72 дм2.
8. На молочном комбинате «Кубанская Бурёнка» изготовили 4700 л молочной продукции. Молока изготовили 2700 л, кефира – в три раза меньше, чем молока, остальная продукция – ряженка. Какой молочной продукции изготовили больше – ряженки или кефира и на сколько?
9. В таблице изображены четыре фигуры. Укажи, в какой клетке неверная фигура:
|
Есть прямой угол
|
Нет прямого угла
|
Треугольник
|
1 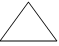
|
2 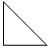
|
Четырёхугольник
|
3 
|
4 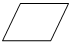
|
Ответ: ___________.
|
Задают вопросы по содержанию диагностической работы. Самостоятельно выполняют задания работы по вариантам.
Ответы:
1. 3) 200 048.
2. 14243.
3. 1724.
4. 2) 2069.
5. 1) 2220 кг.
6. 4) 279.
7. Решение:
1) 2 · 2 = 4 (м2) – площадь коврика.
2) 20 – 4 = 16 (м2) – остальная площадь комнаты.
Ответ: 3) 16 м2.
8. 1) 2700 : 3 = 900 (л) – кефира.
2) 2700 + 900 = 3600 (л) – молока и кефира.
3) 4700 – 3600 = 1100 (л) – ряженка.
4) 1100 – 900 = 200 (л) – больше ряженки.
9. 2 – 1
|
Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей.
Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор.
Выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий. Осуществлять контроль по результату
|
Вариант 2
|
1. Как записать цифрами число триста восемь тысяч три?
1) 380 003; 2) 308 003; 3) 308 030; 4) 3 008 003.
2. Найди значение суммы чисел 4583 и 30759.
3. Найди значение разности чисел 5028 и 3899.
4. Найди значение частного чисел 35075 и 5.
1) 7510; 2) 7015; 3) 7115; 4) 5751.
5. Знак на весах указывает, что на них можно взвешивать груз не более 2 т 500 кг. Укажи вес груза, который можно взвесить на этих весах:
1) 2490 кг; 2) 3 т; 3) 3 т 230 кг; 4) 2590 кг.
6. Найди значение выражения
(98 : 14 + 70 : 2) ∙ 60.
1) 2025; 2) 1078; 3) 2520; 4) 987.
7. В комнату, длина которой 8 м, а ширина 6 м, постелили ковёр площадью 12 м2. Какая площадь комнаты осталась не занятой ковром?
1) 48 м2; 2) 36 м; 3) 20 м2; 4) 36 м2.
8. В компьютерной игре надо набрать 500 очков. Саша на первом этапе набрал в 2 раза меньше очков, чем на третьем этапе, на втором этапе набрал 130 очков. Выиграл ли Саша, если на третьем этапе он набрал 250 очков?
9. В таблице изображены четыре фигуры. Укажи, в какой клетке неверная фигура:
|
Есть прямой угол
|
Нет прямого угла
|
Треугольник
|
1 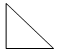
|
2 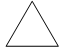
|
Четырёх-угольник
|
3 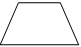
|
4 
|
|
Ответы:
| |
|
|
 Скачать 0.67 Mb.
Скачать 0.67 Mb.