Маркетинговые показатели. 1 Что такое система показателей
 Скачать 19.01 Mb.
|
|
Таблица 7.2 Показатели эластичности в точке, рассчитанной по величине наклона функции ПРИМЕР. Хави занимается маркетингом одной марки зубной пасты. Он знает, что динамика продаж этой марки отображается кривой линейного спроса. При текущей цене в 3 доллара за штуку его компания продает в настоящее время 60 ООО единиц пасты с показателем эластичности -2,5. Было внесено предложение поднять цену до 3,18 доллара за единицу с тем, чтобы стандартизировать показатели маржи брендов. Сколько будет продано единиц товара при цене в 3,18 доллара? Предлагаемое изменение до 3,10 доллара соответствует 6-процентному увеличению нынешней цены в размере 3 долларов. Так. как показатель эластичности составляет —2,5, можно предположить, что такое увеличение приведет к уменьшению объема штучных продаж на 2,5 х 6 или на 15%. Сокращение текущих продаж в объеме 60 ООО товарных единиц на 15% даст в итоге новое количество в размере 0,85 х 60 000, или 51 000 товарных единиц. Постоянная эластичность: кривая спроса с постоянно изменяющимся наклоном Вторая распространенная форма зависимости, которая используется для определения спроса, связана с постоянной эластичностью3. Эта зависимость называется «кривой спроса», так как она действительно имеет изогнутую форму. В отличие от функции линейного спроса условия в данном варианте прямо противоположны: величина эластичности постоянна, тогда как величина наклона изменяется в каждой точке. Основополагающим допущением, лежащим в основе кривой спроса с постоянной эластичностью, является то, что незначительное процентное изменение цены вызывает такое же процентное изменение количества продаж товарных единиц, вне зависимости от величины исходной цены. То есть темп изменения количества в зависимости от изменения цены, выраженный как соотношение процентных показателей, равен постоянной величине по всей кривой. Этой постоянной величиной является эластичность. В математическом выражении на кривой спроса с постоянной эластичностью величина наклона, умноженная на цену, разделенную на количество, равна постоянной величине (эластичности) для всех точек по всей кривой (см. рис. 7.5). Функция постоянной эластичности может быть также выражена уравнением, которое легче рассчитывать в электронных сводных таблицах: Q(P) = AxP*Jiac Кривая постоянной эластичности INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image8.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image8.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image8.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image8.jpeg" \* MERGEFORMAT 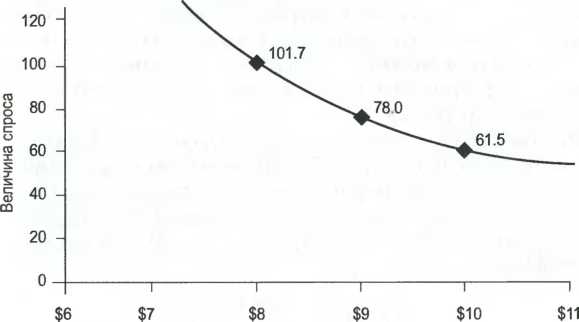 Цена Рис. 7.5. Постоянная эластичность В этом уравнении EЛAC - это ценовая эластичность спроса. Обычно она выражена отрицательной величиной. А - это поправочный коэффициент. Он может рассматриваться как количество, которое было бы продано по цене 1 доллар (при допущении, что 1 доллар - это оптимальная цена на исследуемый продукт). ПРИМЕР. Построим кривую спроса с постоянной эластичностью -2,25 и поправочным коэффициентом 10 943,1. Для каждой точки на этой кривой незначительное процентное повышение цены даст в результате процентное сокращение количества проданных товарных единиц, где последнее будет больше первого в 2,25 раза. Этот коэффициент 2,25 сохраняется, однако, только для очень незначительных процентных изменений цены, так как величина наклона изменяется в каждой точке. Использование коэффициента 2,25 для прогнозирования результатов окончательного процентного повышения цены всегда дает только приблизительную величину. Кривая, построенная в данном примере, должна выглядеть как кривая постоянной эластичности, представленная на рис. 7.5. Более точные цифры спроса при ценах 8, 9 и 10 долларов будут равны соответственно 101 669, 78 ООО и 61 538 товарным единицам. Постоянная эластичность в некотором роде аналогична непрерывным процентным начислениям. На кривой с постоянной эластичностью каждое незначительное процентное повышение цены вызывает такое же процентное сокращение количества продаваемых товарных единиц. Эти процентные сокращения складываются с постоянным коэффициентом, что приводит к тому, что совокупное процентное сокращение не может точно отождествляться с постоянным коэффициентом. П 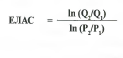 о этой причине, взяв любые две точки на кривой спроса с постоянной эластичностью, мы больше не можем рассчитывать эластичность, используя конечные показатели разницы, как мы могли делать это в случае с линейной кривой спроса. Вместо этого следует использовать более сложную формулу на базе натуральных логарифмов.ПРИМЕР. Взяв любые две точки на предыдущей кривой спроса с постоянной эластичностью, мы можем подтвердить, что показатель эластичности составляет -2,25. При цене в 8 долларов количество проданных единиц товара составляет
При цене в 9 долларов количество проданных единиц товара составляет 78 ООО. Назовем эти показатели Р2 и Qr Вставив эти Цифры в нашу формулу, мы определим, что ЕЛАС = In (7800/101669)/ln (9/8) = -0,265/0,118 = - 2,25 Нели бы мы установили показатель Р2 равным 8 долларам, а показатель р — 9 долларам, то мы бы получили точно такой же показатель эластичности. По сути, вне зависимости от того, какие две точки на этой кривой с постоянной эластичностью мы выбираем, и безотносительно к порядку, в котором они рассматриваются, показатель эластичности всегда будет -2,25. Суммируя все вышесказанное, можно сказать, что эластичность является стандартным показателем чувствительности рынка к изменениям цен. В общем, она представляет собой процентную величину наклона функции (кривой) спроса, полученную путем умножения величины наклона кривой для данной цены на соотношение цены и количества проданных товарных единиц. Р Эластичность (Р) = Величина наклона х Q Эластичность можно также рассматривать, как процентное изменение количества при незначительных изменениях цен. На линейной кривой спроса величина наклона является постоянной, но эластичность изменяется вместе с ценой. В этом случае маркетологи могут использовать эластичность для расчета результатов ценовых изменений в обоих направлениях, но они должны использовать такую эластичность, которая соответствует их исходному ценовому ориентиру. Причина: на линейной кривой спроса значения эластичности варьируется по ценовым точкам, но предполагаемые показатели, основанные на этих значениях, являются точными. На кривой спроса с постоянной величиной эластичности последняя одинакова во всех ценовых точках, но предполагаемые показатели, основанные на этих величинах, будут приблизительными. Предположив, что они определены точно, использование самой кривой спроса с постоянной эластичностью для прогнозирования объема продаж на основе ценовых изменений будет более точным. Источники данных, сложности и предостережения Ценовая эластичность обычно определяется с помощью имеющихся данных. Эти данные могут быть получены на основании фактических продаж и ценовых изменений, наблюдаемых на рынке, совместных исследований намерений клиентов, опросов потребителей об их ценах покупателя, или части покупателей, согласных с ценой, или на основании результатов тестирования пробных рынков. При расчете эластичности зависимости «цена-количество» могут быть схематично построены на бумаге, определены на базе регрессий в виде уравнений с линейной или постоянной эластичностью, или определены с помощью более сложных построений, которые включают в себя другие переменные величины из комплекса маркетинга, например, рекламу или качество товара. Чтобы подтвердить обоснованность и пригодность этих методик, маркетологи должны ясно представлять себе влияние полученных предварительных оценок эластичности на поведение клиентов. Обладая таким пониманием, маркетологи могут определить, имеют ли их предварительные оценки какой-либо смысл, или они требуют дальнейшего подтверждения. Сделав это, можно переходить к следующему этапу для принятия решений в сфере ценообразования.
линейного и постоянного спроса Оптимальная цена - это наиболее прибыльная цена любого продукта. На линейной кривой спроса оптимальная цена располагается посередине между максимальной ценой покупателя и переменными издержками на производство продукта. Изменить: резервированная цена - на цена покупателя, расходы - на издержки Оптимальная цена для = [Максимальная цена покупателя ($) + линейной кривой сиро- Переменные издержки ($)] са ($) 2 Обычно валовая прибыль от реализации определенного продукта по оптимальной цене представляет собой обратную величину его ценовой эластичности со знаком минус. -1 Валовая прибыль при оптимальной цене (%) = —— Эластичность (I) Хотя применение данного соотношения может представлять определенные трудности, оно дает глубокое понимание сути вопроса: на кривой спроса с постоянной эластичностью оптимальная маржа напрямую зависит от эластичности. Это значительно упрощает определение оптимальной цены на продукт с известными переменными издержками на его производство. Цель: определить цену, которая способствует получению наибольшей валовой прибыли Хотя оптимальная цена может быть определена несколькими способами, приемлемой отправной точкой может служить цена, которая способствует получению наибольшей валовой прибыли от реализации данного продукта после вычета переменных издержек - то есть цена продукта, обеспечивающая наибольшую прибыль. Если менеджеры назначают слишком низкую цену, они отказываются от дохода, который могли бы получить за счет клиентов, готовых заплатить больше. Кроме того, низкая цена может стать причиной того, что покупатели будут оценивать продукт ниже в сравнении с оценкой, которую он мог бы получить при иных обстоятельствах. То есть это приведет к уменьшению их цены покупателя. И наоборот, если менеджеры назначают слишком высокую цену, они рискуют потерять прибыль от клиентов, которых вполне могли бы обслужить и получить при этом доход. Конструкция При линейном спросе оптимальная цена находится посередине между максимальной ценой покупателя и переменными издержками на производство продукта. На линейной кривой спроса цена, которая максимально увеличивает совокупную валовую прибыль от продукта, всегда располагается точно посередине между максимальной ценой покупателя (MRP) и переменными затратами на его производство. В математическом смысле, если Р* представляет оптимальную цену продукта, то MRP является отрезком, откладываемым на оси X линейной кривой спроса, a VC - переменными издержками на единицу продукта: Px = (MRP+ VC)/ 2 ПРИМЕР. Компания Джейми продает товары, себестоимость которых составляет 1 доллар за штуку. Спрос носит линейный характер. Джейми считает, что если установить цену на уровне 5 долларов, ему не удастся продать ни одной единицы товара. Он полагает, что при сокращении цены на один Доллар будет продаваться одна дополнительная товарная единица. С учетом того, что переменные издержки составляют 1 доллар, максимальная цена покупателя - 5 долларов, а кривая спроса является линейной, Джейми вправе предположить, что он получит максимальную валовую прибыль при цене, находящейся посередине между VC и MRP. То есть оптимальная цена составит (5 долларов + 1 доллар)/2 или 3 доллара (см. рис. 7.6)4. При использовании линейной кривой спроса менеджерам необязательно знать количественную величину спроса на товар, чтобы определить оптимальную цену. Те, кто хочет проверить цифры валовой прибыли Джейми, могут найти подробные данные в табл. 7.3. Максимальная совокупная валовая прибыль после построения «квадрата» INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image10.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image10.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image10.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image10.jpeg" \* MERGEFORMAT 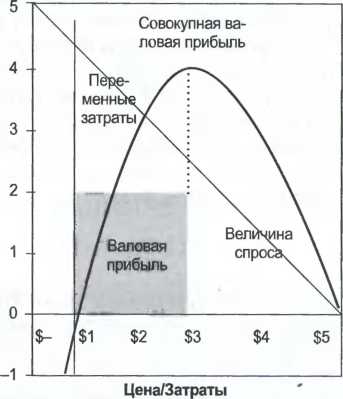 Рис. 7.6. Оптимальная цена лежит посредине между переменными затратами и MRP Таблица 7.3. Оптимальная цена = Уг (MRP + Переменные издержки)
или итоговую валовую прибыль. Чтобы определить оптимальную валовую прибыль, менеджеры могут использовать следующее уравнение: Валовая прибыльх = (MWB/MRP) х (Рх – VC)2 ПРИМЕР. Джейми разрабатывает новый, но схожий с предыдущим, продукт. Спрос на него выражается линейной функцией, где максимальную готовность к покупке (MWB) проявляют 200 человек, а максимальная цена продавца (MRP) составляет 10 долларов. Переменные издержки составляют 1 доллар на единицу продукта. Джейми знает, что его оптимальная цена будет располагаться посередине между MRP и переменными затратами. То есть она должна быть (1 доллар +10 долларов) = 5,50 доллара за единицу продукта. Используя формулу для расчета оптимальной валовой прибыли, Джейми рассчитал совокупную валовую прибыль, извлекаемую при оптимальной цене: Валовая прибыль при оптимальной цене для линейной функции спроса ($) = [MWB (#)/MRP ($)] х [Цена ($) - Переменные затраты ($)] А2 = (200/10) х (5,50 долларов - 1 доллар)А2 = 20 х 4,5 доллараА2 = 405 долларов Джейми составил сводную таблицу, которая подтверждает эти расчеты (см. табл. 7.4). Таблица 7.4. Валовая прибыль, увеличенная до максимума при оптимальной цене
Это соотношение сохраняется по всей линейной кривой спроса, вне зависимости от величины наклона. Следовательно, для такой кривой можно рассчитать оптимальную цену продукта на основании только двух вводных параметров: переменных издержек на единицу продукта и максимальной цены покупателя. ПРИМЕР. Для каждого из брендов А, В и С переменные издержки составляют 2 доллара на единицу продукта, а спрос на них выражается линейной зависимостью, как это показано в табл. 7.5. Таблица 7.5. Формула расчета оптимальной цены применима ко всем линейным зависимостям спроса
На основании этих вводных параметров мы можем определить максимальную цену покупателя - самую низкую цену, при которой спрос равен нулю. Мы знаем, что спрос на бренд С, например, выражается линейной зависимостью, в которой количество продаж сокращается на одну единицу при повышении цены на 1 доллар. Если при цене 12 долларов спрос составляет шесть единиц товара, то самой низкой ценой, при которой никто не купит ни одной единицы, будет 18 долларов. Это и есть максимальная цена покупателя. Мы можем провести аналогичные расчеты для брендов А и В (см. табл. 7.6). Таблица 7.6. При линейной зависимости спроса определение оптимальной цены требует только двух вводных параметров '
Хот факт, что оптимальные цены, определенные таким образом, дадут максимально возможную валовую прибыль, отражен в табл. 7.7. Таблица 7.7. Подтверждение оптимальных цен при линейной зависимости спроса
Поскольку величина наклона не влияет на оптимальную цену, все функции спроса с максимальной ценой покупателя и переменными издержками дадут в итоге одну и ту же оптимальную цену. ПРИМЕР. Изготовитель диванных подушек работает на трех разных рынках - городском, пригородном и сельском. Они сильно отличаются по емкости. В городе спрос гораздо выше, чем в пригороде или в сельской местности. Переменные издержки, однако, на всех рынках одинаковы, и составляют 4 доллара на единицу продукции. Максимальная цена покупателя в размере 20 долларов за штуку также едина для всех трех рынков. Вне зависимости от емкости рынка оптимальная цена составляет, таким образом, 12 долларов на единицу продукции на всех трех рынках (см. рис. 7.7 и табл. 7.8). Оптимальная цена в размере 12 долларов подтверждена расчетами, представленными в табл. 7.9. INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image11.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image11.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image11.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image11.jpeg" \* MERGEFORMAT 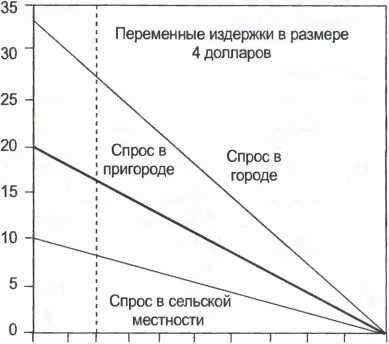 Различные величины наклона линейных зависимостей спроса с одинаковыми показателями MWP и VC о О. Рис. 7.7. Зависимости линейного спроса с одинаковыми значениями MWP и переменными издержками | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||