Маркетинговые показатели. 1 Что такое система показателей
 Скачать 19.01 Mb.
|
|
Таблицу количества единиц товара, которое предполагается продать по каждой из нескольких цен, часто называют таблицей спроса (или кривой спроса). Этот пример показывает, что одним из способов построения кривой спроса является суммирование индивидуальных цен покупателя. Хотя совершенно ясно, что на практике сложно определить индивидуальные цены покупателя, мы просто хотели показать, как можно их использовать в процессе принятия решений. В этом примере оптимальная цена - то есть цена, которая способствует максимальной валовой прибыли - составляет 100 долларов. По такой цене изготовитель надеется продать четыре единицы товара. Маржинальная прибыль от продажи каждой единицы составляет 40 долларов, что дает в итоге общую валовую прибыль в размере 160 долларов. Этот пример также иллюстрирует понятие потребительского излишка. При цене в 100 долларов изготовитель продает три единицы продукции по стандартной цене, которая ниже цен покупателей. Потребитель, для которого цена покупателя составляет 110 долларов, будет иметь излишек в размере 10 долларов. Потребитель, для которого цена покупателя составит 120 долларов, воспользуется излишком в сумме 20 долларов. И, наконец, потребитель, у которого установилась самая высокая цена покупателя - 130 долларов - получит излишек в размере 30 долларов. С точки зрения изготовителя совокупный потребительский излишек - 60 долларов - дает возможность увеличения валовой прибыли, если он сможет найти способ извлечения этих невостребованных средств. • Источники данных, сложности и предостережения Определение цен потребителя - дело не простое. Чтобы лучше разобраться с этим показателем, часто используются следующие две методики:
Такие исследования, однако, сложно организовать, а во многих случаях их невозможно провести. Следовательно, в качестве резервной методики маркетологи могут использовать метод определения части покупателей, согласных с ценой. Вместо того, чтобы пытаться узнать цену покупателя по каждому клиенту, они могут пойти по более легкому пути и исследовать всего несколько выбранных цен, поинтересовавшись у респондентов, считают ли они, что данный продукт стоит этих денег. Линейный спрос Таблица соотношений «цена-количество», составленная из данных о ценах покупателя, может принимать самые разнообразные формы. В случае, если распределение цен покупателя равномерное - когда резервированные цены располагаются на шкале с равными промежутками, - таблица спроса будет линейной (см. рис. 7.1). То есть каждое приращение в цене будет сокращать количество на одинаковую величину. Величина Максимальная готовность к покупке (MWB) INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image4.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image4.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image4.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image4.jpeg" \* MERGEFORMAT 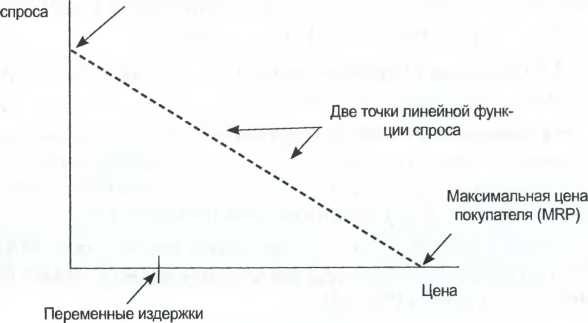 Рис. 7.1. Максимальная готовность купить и максимальная цена покупателя Так как на сегодняшний день линейная функция является, несомненно, самым распространенным методом отображения спроса, мы опишем данную функцию в той мере, в которой она иллюстрирует распределение лежащих в ее основе цен покупателя. Чтобы построить прямую линию, необходимо взять всего две точки. Подобным же образом, чтобы записать уравнение для этой прямой, необходимо всего два параметра. Обычно это уравнение записывается таким образом: Y = тХ + Ь, где т — это наклон линии, а b - отрезок, откладываемый на оси Y. Прямая линия, однако, может также определяться двумя точками в местах пересечения осей. В случае линейного спроса эти точки пересечения (откладываемые отрезки) дают руководству важные сведения. Отрезок, откладываемый на оси «величина спроса», может рассматриваться как отражение максимальной готовности к покупке (MWB). Это общее число потенциальных покупателей данного продукта. Компания может обслужить всех этих покупателей только при нулевой цене. Если допустить, что каждый потенциальный покупатель приобретает одну единицу товара, то MWB - это количество проданных единиц товара при нулевой цене. Отрезок, отсекаемый по оси «цена», может рассматриваться как максимальная цена покупателя (MRP). MRP представляет собой число, немного превышающее наивысшую цену покупателя для всех тех, кто выражает готовность совершить покупку. Если компания устанавливает цены на свой товар на уровне не ниже MRP, то количество совершенных покупок будет нулевым. Максимальная цена покупателя. Наименьшая цена, при которой величина спроса равна нулю. Максимальная готовность к покупке (MWB). Количество единиц товара, которое потребитель готов «купить», когда цена на товар равна нулю. Это искусственное понятие, используемое для привязки линейной функции спроса. На линейной кривой спроса, определенной показателями MWB и MRP, уравнение количества (Q) как функция цены (Р) может быть записано следующим образом: К = (MWB) х [1 - (P/MRP)] ПРИМЕР. Эйрин знает, что спрос на ее прохладительные напитки выражается простой линейной функцией цены. Она может продать 10 товарных единиц по нулевой цене. Когда цена достигает 5 долларов за единицу, спрос падает до нуля. Сколько единиц своей продукции сможет продать Эйрин, если цена будет 3 доллара (см. рис. 7.2)? Линейный спрос: цена и величина спроса INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image5.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image5.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image5.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image5.jpeg" \* MERGEFORMAT 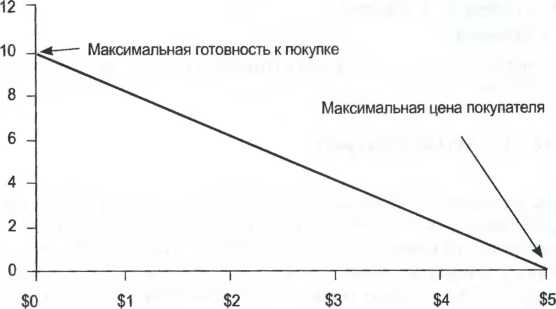 Цена Рис. 7.2. Простая линейная кривая спроса Для прохладительных напитков Эйрин величина MRP (максимальной цены покупателя) составляет 5 долларов, а показатель MWB (максимальной готовности к покупке) - 10 товарных единиц. При цене в 3 доллара Эйрин сможет продать 10х(1-3/5 долларов), или 4 единицы продукции. П 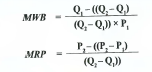 ри линейном спросе для определения величин MWB и MRP могут быть использованы любые две точки по функции спроса «цена-количество». Если Ц и К} являются первыми точками «цена- количество», ъ. Ц2w К2 — вторыми, тогда для расчета значений MWB и MRP могут быть использованы следующие два уравнения:—ш ПРИМЕР. В начале этой главы мы уже рассматривали пример компании, которая продает 5 товарных единиц по цене 90 долларов за штуку и три единицы по цене 110 долларов. Какими будут значения MWB и MRP при линейном спросе? MWB = 5 - (-2/20 долларов) х 90 долларов = 5 + 9 = 14 MRP = 90 долларов - (20 долларов/-2) х 5 = 90 долларов + 50 долларов = 140 долларов Уравнение для количества как функции цены будет выглядеть, соответственно, так: К = 14 х (1 - (Р/140 долларов)) Рынок в данном примере, как вы помните, состоит из 11 потенциальных покупателей, цены покупателя для которых составляют 30, 40 ... 120 и 130 долларов. При цене в 130 долларов компания продает одну товарную единицу. Если мы подставим цену, равную 130 долларам, в предыдущее уравнение, то в результате расчета количество будет действительно равно единице. Чтобы сохранить это условие, величина MRP должна быть немного больше 130 долларов. Линейная функция спроса часто дает корректное приближение фактической величины спроса только в ограниченном диапазоне цен. Например, на нашем рынке, состоящем из 11 человек, спрос является линейным только для цен в диапазоне от 30 до 130 долларов. Однако чтобы записать уравнение линейной функции, которая описывает спрос в диапазоне от 30 до 130 долларов, мы должны использовать показатель MWB в количестве 14, a MRP - в размере 140 долларов. При использовании данного линейного уравнения мы должны помнить, что оно отражает фактический спрос только для цен в диапазоне от 30 до 130 долларов, как это показано на рис. 7.3. 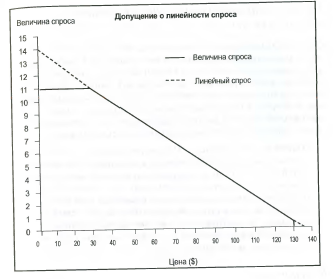 Рис. 7.3. Пример линейной кривой спроса
Ценовая эластичность оценивает чувствительность величины спроса к небольшим колебаниям цены. Изменение количества (%) Ценовая эластичность (I) = — Изменение цены (%) Ценовая эластичность может быть ценным инструментом, позволяющим маркетологам устанавливать оптимальные цены. Цель: понять чувствительность рынка к изменениям цен Ценовая эластичность является широко распространенным показателем чувствительности рынка к изменениям цен. Многие маркетологи, однако, используют этот термин без четкого понимания того, что он из себя представляет. Данный раздел поможет прояснить некоторые потенциальные опасности, связанные с оценкой ценовой эластичности. Это сложный материал, но он стоит потраченных на его изучение усилий. Грамотное управление эластичностью цен поможет маркетологам устанавливать оптимальные цены. Ценовая эластичность. Чувствительность спроса к незначительным изменениям цен, выраженная в процентном соотношении. Если приблизительно рассчитанная ценовая эластичность составляет, например, —1,5, тогда мы вправе предположить, что процентное изменение количества будет приблизительно в полтора раза больше, чем процентное изменение цены. Тот факт, что это число отрицательное, указывает на то, что при росте цены величина спроса будет падать, и наоборот. Конструкция Если мы поднимет цену на продукт, должны ли мы ожидать, что спрос сохранится на прежнем уровне, или же он резко упадет? Мы называем спрос неэластичным на рынках, которые нечувствительны к изменениям цен. Если незначительные ценовые изменения сильно сказываются на спросе, мы говорим, что спрос эластичный. Большинству из нас не представляет сложности понять эластичность на качественном уровне. Трудности появляются тогда, когда мы пытаемся определить это важнейшее понятие в количественных показателях. Сложность №1: вопросы полярности знака Первая сложность, связанной с эластичностью, заключается в согласовании полярности ее знака. Эластичность представляет собой соотношение процентного изменения величины спроса и процентного изменения цены, когда данное ценовое изменение незначительно. Если повышение цены влечет за собой увеличение количества, то этот коэффициент будет отрицательным. Следовательно, эластичность всегда будет отрицательной величиной. Многие, однако, придерживаются такого мнения, что количество продаж всегда идет вниз по мере увеличения цен и сразу же переходят к вопросу «Насколько?». Ответом на этот вопрос служит ценовая эластичность, которая является в таком случае положительной величиной. По их мнению, если эластичность выражена коэффициентом 2, то некоторое процентное повышение цены приведет к вдвое большему сокращению количества продаж. В данной книге, при таком развитии событий, мы бы сказали, что коэффициент ценовой эластичности составляет -2. Сложность №2: при линейном спросе эластичность ИЗМЕНЯЕТСЯ ВМЕСТЕ С ИЗМЕНЕНИЕМ ЦЕНЫ Для линейной функции спроса величина наклона будет постоянной, а эластичность - нет. Причина: эластичность и величина наклона - это не одно и то же. Величина наклона представляет собой изменение количества при незначительном изменении цен. Эластичность же, наоборот, является процентным изменением количества при небольших процентных изменениях цен. ПРИМЕР. Рассмотрим три точки на линейной кривой спроса: (8 долларов, 100 единиц), (9 долларов, 80 единиц) и (10 долларов, 60 единиц); см. рис. 7.4. Изменение цены на один доллар приводит к изменению количества на 20 товарных единиц. Величина наклона этой кривой является постоянной -20 товарных единиц на доллар. При росте цены с 8 до 9 долларов (рост 12,5%) количество сокращается со 100 до 80 товарных единиц (20-процентное сокращение). Соотношение этих процентных показателей будет таким: 20%/12,5%, или-1,6. Таким же образом, при росте цены с 8 до 10 долларов (25-процентное повышение) количество сократится со 100 до 60 товарных единиц (40-процентное сокращение). Соотношение 40%/25% опять таки будет -1,6. По-видимому, соотношение процентного изменения количества и процентного изменения цены составляет -1,6 вне зависимости от масштаба изменений цены в 8 долларов. Рассмотрим, что происходит, когда цена повышается с 9 до 10 долларов (рост 11,11%). Количество товарных единиц сокращается с 80 до 60 (25- процентное сокращение). Таким образом, соотношение этих цифр, 25%/
Ю Маркетинговые показатели INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image7.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image7.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\HP\\Desktop\\media\\image7.jpeg" \* MERGEFORMATINET INCLUDEPICTURE "media/image7.jpeg" \* MERGEFORMAT 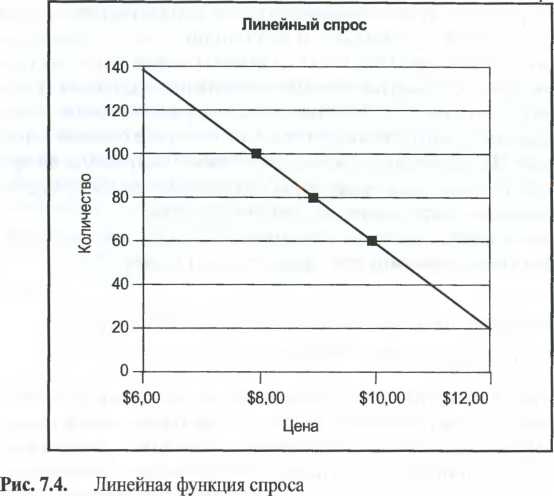 ние составит-2,25 при цене в 9 долларов вне зависимости от направления любого ценового изменения. Пример расчета. Подтвердим, что соотношение процентного изменения количеств и процентного ценового изменения при цене 10 долларов составляет -3,33 для любого возможного изменения цены. На линейной кривой спроса эластичность изменяется вместе с изменением цены. По мере роста цены увеличивается величина эластичности. Таким образом, для линейной кривой спроса соотношение абсолютного изменения количества на товарную единицу и абсолютного изменения цены на денежную единицу (наклон кривой) будет постоянным, тогда как соотношение процентного изменение количества и процентного изменения цены (эластичность) таковым не будет. Спрос становится более эластичным - то есть отрицательная направленность величины эластичности увеличивается во все большей степени - по мере роста цены. Для линейной кривой спроса эластичность спроса может быть рассчитана, по меньшей мере, тремя способами:  Чтобы акцентировать ваше внимание на том, что эластичность изменяется с изменение цены на линейной кривой спроса, мы пишем «Эластичность (Р)», отражая тем самым тот факт, что эластичность является функцией цены. Мы также используем термин «точечная эластичность», чтобы подкрепить мысль о том, что данная эластичность относится только к одной точке на линейной кривой спроса. Таким же образом, потому, что наклон линейной кривой спроса представляет собой изменение количества при заданном изменении цены, ценовая эластичность для линейной кривой спроса будет равна величине наклона, умноженной на цену, разделенной на количество. См. третье из представленных выше уравнений. ПРИМЕР. Возвращаясь к предыдущей функции спроса, мы видим, что наклон кривой отражает падение спроса на 20 товарных единиц при уменьшении цены на один доллар. То есть величина наклона равна -20. Формула наклона кривой эластичности может использоваться для подтверждения наших предыдущих расчетов. Вычислите цену/количество в каждой точке и умножьте эту цифру на величину наклона с тем, чтобы получить ценовую эластичность в данной точке (см. табл. 7.2). Например, при цене в 8 долларов количество проданного товара составляет 100 единиц. Следовательно: Эластичность (8 долларов) = -20 х (8/100)
= -1,6 | |||||||||||||||||||||||||