1. Общественное здоровье и здравоохранение как наука и предмет её изучения. Общественное здоровье и здравоохранение
 Скачать 2.89 Mb. Скачать 2.89 Mb.
|
|
n / 2; если нечетное: (n + 1) / 2. ПРИМЕР: Распределение обследованных рабочих по частоте пульса.
Виды вариационных рядов: 1. Ранжированный (упорядоченный) ряд – такой, в котором числовые значения вариант располагаются последовательно, по убыванию или по возрастанию (5, 7, 8, 12, 25 и т.д.); 2. Неранжированный ряд – такой, в котором вариант располагаются беспорядочно (34, 6, 12, 45 и т.д.); 3. Прерывный (дискретный) ряд – такой, в котором варианты выражены только целым числом и не могут иметь промежуточных значений (число детей в семье, число лейкоцитов в крови, частота пульса, число посещений и пр.); 4. Непрерывный ряд – такой, в котором варианты могут принимать любые значения, в том числе и дробные (рост, масса тела, время, затраченное на прием одного больного, содержание в крови или воздухе различных веществ и т.д.); 5. Простой (развернутый) ряд – такой, в котором каждая варианта и соответствующая ей частота обозначены отдельно. Ряд, в котором каждая варианта встречается с частотой, равной единице, называется простым невзвешенным, а если с разной частотой – простым взвешенным. 6. Сгруппированный (интревальный) ряд – такой, в котором варианты соединены в группы, объединяющие их по величине в пределах определенного интервала. Составление сгруппированного вариационного ряда. Простой, несгруппированный ряд, особенно при большом объеме совокупности, является громоздким и неудобным для вычисления средних величин, поэтому он обычно составляется при небольшом числе наблюдений (n < 30). При большом числе наблюдений (n > 30) строят сгруппированный ряд на основе интервала (i), показывающего число вариант, объединенных в одну группу. Группировку рядов проводят следующим образом: 1. Определяют размах ряда (амплитуду) вычитанием минимальной варианты из максимальной; 2. Полученное число делят на желаемое количество групп – так определяется интервал; 3. Начиная с минимальной варианты, строят вариационный ряд. Границы интервалов должны быть четкими, исключающими попадание одной и той же варианты в разные группы. Правильно составленный сгруппированный (интервальный) ряд должен отвечать следующим требованиям: 1. Все варианты распределения должны войти в группы; 2. Общее число выделенных групп должно быть не менее 7 (иначе вычисленная средняя арифметическая будет неточной) и не более 15 (иначе ряд будет большим и громоздким); 3. Каждая новая последующая группа должна начинаться с новой последующей варианты, т.е. одна и та же варианта не должна встречаться в двух смежных группах. 4. Интервал должен быть одинаковым в каждой группе, т.е. в каждую группу должно входить одинаковое число вариант. Размер интервала определяют, исходя из характера изучаемого признака, из числа выбранных групп, количества вариант и числа наблюдений. Величина интервала выбирается также с учетом целей и задач исследования. 5. Каждая группа в сгруппированном ряду должна иметь начальную и конечную варианты, т.е. не должно быть так называемых открытых групп (например, до 5 лет, старше 60 лет и т.п.). 6. Каждой группе присваивается частота, равная сумме частот всех вариант, вошедших в группу. Упрощение сгруппированного ряда заключается в предварительном определении середины интервала (центральной варианты). В прерывных сгруппированных вариационных рядах центральная варианта определяется как полусумма начальной и конечной вариант в группе и ей присваивается суммарная частота всех вариант, вошедших в данную группу. В непрерывных сгруппированных вариационных рядах центральная варианта определяется как полусумма начальных вариант соседних групп. Средняя арифметическая (М) – производная вариационного ряда, которая одним числом характеризует весь ряд и выражает его основную закономерность. 1. Вычисление простой и взвешенной средней арифметической. Средняя арифметическая простая вычисляется для простого невзвешенного вариационного ряда, в котором варианты встречаются с частотой, равной единице (Р = 1), и определяется как сумма всех вариант (ЕV), деленная на число наблюдений (n): M = ∑V / n, где M – средняя арифметическая, V – варианты, ∑ – знак суммирования, n – число наблюдений. ПРИМЕР: Содержание сахара в крови (в мг %).
M = ∑V / n = 1000 / 10 = 100 мг % Средняя арифметическая взвешенная вычисляется в тех случаях, когда в вариационном ряду отдельные значения вариант повторяются (P > 1). M = ∑VP / n, где М – средняя арифметическая, V – варианты, Р – частоты, ∑ – знак суммирования, n – число наблюдений. ПРИМЕР: Результаты измерения массы тела юношей 18 лет.
M = ∑VP / n = 1540 / 25 = 61.6 кг 2. Вычисление средней арифметической по способу моментов (условных отклонений). При больших числовых значениях признака в значительных по объема совокупностях средняя арифметическая вычисляется упрощенным способом, который называется «способ моментов» или «способ условных отклонений». Вычисление средней арифметической по способу моментов основано на следующих ее свойствах: 1. Каждая варианта отклоняется от средней в большую или в меньшую сторону. Это отклонение (d) может быть выражено положительным или отрицательным числом. 2. Сумма отклонений с положительным знаком всегда равна сумме отклонений с отрицательным знаком, следовательно, алгебраическая сумма отклонений всех вариант от средней равна нулю (это свойство средней лежит в основе данного способа вычисления). 3. Средняя арифметическая равна любой произвольно взятой величине плюс среднее отклонение от нее всех членов ряда, которое имеет выражение ∑Pd / n и называется моментом первой степени (обозначается буквой А). Средняя арифметическая вычисляется по формуле: M = M1 + ∑dP / n, где М – средняя арифметическая, М1 – «условная» средняя арифметическая, d – отклонение условной средней от вариант, Р – частота, n – число наблюдений, ∑ - знак суммирования. Вычисление ведется от «условной» средней (М1). За среднюю условно принимается любая варианта, чаще мода (как наиболее часто встречающаяся варианта). Если эта величина действительно средняя арифметическая, то сумма отклонений всех вариант от нее будет равна нулю. Если сумма отклонений будет равняться какой-то величине, то это означает, что «условная» средняя не соответствует действительной и к ней требуется поправка (момент первой степени – А): Если А = ∑Pd / n, тогда М = М1 + А. ПРИМЕР: Средняя дневная нагрузка врача-терапевта в поликлинике.
Последовательность вычислений: 1. Выбираем «условную» среднюю М1 = 18 больных; 2. Определяем отклонение (d) каждой варианты от «условной средней»: d = V – M1; 3. Найденные отклонения умножаем на частоты: P x (V – M1) = Pd; 4. Вычисляем алгебраическую сумму всех отклонений ∑Pd = - 4; 5. По формуле определяем среднюю арифметическую: M = M1 + ∑Pd / n; M = 18 + (- 4) / 22 = 18 + (- 0,18) = 17,82. 11. Меры изменчивости вариант (амплитуда, среднеквадратичное отклонение, коэффициент вариации). Методика вычисления, сущность, оценка, применение. Средние величины являются важными характеристиками совокупности, однако они полностью не раскрывают индивидуальные значения признака, которые отличаются от средних и различаются между собой. Средние величины скрывают изменчивость, колеблемость признака, его рассеянность. При обработке вариационного ряда недостаточно только лишь вычислить среднюю арифметическую, нужно еще оценить, насколько она типична и достоверна для данной совокупности. Для этого в статистике существуют специальные параметры средней - мера типичности и мера достоверности. Оценка типичности средней арифметической. Чем вариационный ряд более компактен, менее рассеян, тем лучше средняя арифметическая характеризует данную совокупность. Если вариационный ряд растянут, отдельные значения вариант сильно отклоняются от средней (т.е. имеется большая вариабельность, колеблемость признака), то средняя хуже характеризует ряд в целом и является менее типичной для данной совокупности Таким образом, кроме средней необходима еще одна характеристика ряда: его колеблемость. Простейшей мерой колеблемости ряда является амплитуда (вариационный размах), т.е. резкость крайних вариант. Например, при подсчете частоты пульса у одной группы обследованных средняя составляла 68, минимальное число было 60, а максимальное - 70. У второй группы средняя частота пульса составляла также 68, но наименьшее число было 55, а наибольшее - 80. Амплитуда в первой группе значительно меньше и, следовательно, все значения группируются вокруг средней. Вторая совокупность более разнообразна, ее рассеянность велика и колебания отдельных значений от средней больше; следовательно, средняя в этой группе менее типична, чем в первой группе. Мерой колеблемости, изменчивости признака и мерой типичности средней арифметической является среднее квадратическое отклонение (сигма - σ), которое определяется по формуле (по способу моментов): 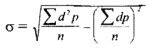 Чем больше среднее квадратическое отклонение, тем выше колеблемость данного вариационного ряда. Для оценки типичности средней арифметической с помощью среднего квадратического отклонения в статистике применяется так называемое «правило трех сигм». Это правило основано на законе нормального распределения и отражает теоретическую закономерность распределения вероятностей случайных событий в условиях бесконечно большого количества наблюдений. Согласно теории вероятности, в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической (М), средним квадратическим отклонеиием (σ) и отдельными значениями вариант существует строгая зависимость: в интервале M+ 1σ находится 68.3% всех вариант ряда, в интервале M+ 2σ – 95.5%, а в интервале M+ 3σ – 99,7%, т.е. практически весь вариационный ряд укладывается в этот предел. Таким образом, среднее квадратическое отклонение является стандартным отклонением, позволяющим предвидеть вероятность появления такого значения изучаемого признака, которое находится в пределах заданных границ. M+ 1σ → 68.3%, M+ 2σ → 95.5%, M+ 3σ → 99,7%. Для того, чтобы проверить, насколько средняя арифметическая типична для той совокупности, из которой она вычислена, нужно к ней прибавить и отнять утроенную сигму (M+ 3σ). Если в полученный интервал данный вариационный ряд укладывается, то средняя типична; если не укладывается – средняя нетипична, совокупность неоднородна и число наблюдений недостаточно. Графическим изображением "правила трех сигм" является кривая нормального распределения (биноминальная кривая Ньютона, кривая Гаусса). Форма этой кривой отражает степень вариабельности результатов наблюдений: при большой разбросанности данных она будет пологой, при малой разбрoсанности – крутой. В силу симметричности кривом перпендикуляр, опушенный из ее максимума на ось абсцисс, пересекает ее в точке, соответствующей среднему значению данных, отложенных по этой оси (М, Мо, Ме). Практическое значение среднего квадратического отклонения: - Сигма характеризует однородность вариационного ряда; - Зная среднюю величину и сигму, можно определить крайние значения вариант и, при необходимости, построит вариационный ряд. Например: среднее артериальное давление у мужчин 30-39 лет было 120 мм рт. ст. при σ = 10 мм. Тогда: Vmin = M – 3σ = 120 – 30 = 90 мм; Vmax = M + 3σ = 120 + 30 = 150 мм. 12. Средняя ошибка средней арифметической и относительной величин: методика вычисления, сущность, оценка. Полученные в результате статистического исследования средние и относительные величины должны отражать закономерности, характерные для всей совокупности. Результаты исследования обычно тем достовернее, чем больше сделано наблюдений, и наиболее точными они являются при сплошном исследовании (т.е. при изучении генеральной совокупности). Однако должны быть достаточно надежные и данные, полученные путем выборочных исследований, т.е. на относительно небольшом числе наблюдений. Различие результатов выборочного исследования и результатов, которые могут быть получены на генеральной совокупности, представляет собой ошибку выборочного исследования, которую можно точно определить математическим путем. Метод ее оценки основан на закономерностях случайных вариаций, установленных теорией вероятности. 1. Оценка достоверности средней арифметической. Средняя арифметическая, полученная при обработке результатов научно-практических исследований, под влиянием случайных явлений может отличаться от средних, полученных при проведении повторных исследований. Поэтому, чтобы иметь представление о возможных пределах колебаний средней, о том, с какой вероятностью возможно перенести результаты исследования с выборочной совокупности на всю генеральную совокупность, определяют степень достоверности средней величины. Мерой достоверности средней является средняя ошибка средней арифметической (ошибка репрезентативности – m). Ошибки репрезентативности возникают в связи с тем, что при выборочным наблюдении изучается только часть генеральной совокупности, которая недостаточно точно ее представляет. Фактически ошибка репрезентативности является разностью между средними, полученными при выборочном статистическом наблюдении, и средними, которые были бы получены при сплошном наблюдении (т.е. при изучении всей генеральной совокупности). Средняя ошибка средней арифметической вычисляется по формуле: - при числе наблюдений больше 30 (n > 30): - при небольшом числе наблюдений (n < 30): Ошибка репрезентативности прямо пропорциональна колеблемости ряда (сигме) и обратно пропорциональна числу наблюдений. Следовательно, чем больше число наблюдений (т.е. чем ближе по числу наблюдений выборочная совокупность к генеральной), тем меньше ошибка репрезентативности. Интервал, в котором с заданным уровнем вероятности колеблется истинное значение средней величины или показателя, называется доверительным интервалом, а его границы – доверительными границами. Они используются для определения размеров средней или показателя в генеральной совокупности. Доверительные границы средней арифметической и показателя в генеральной совокупности равны: |
