1. Общественное здоровье и здравоохранение как наука и предмет её изучения. Общественное здоровье и здравоохранение
 Скачать 2.89 Mb. Скачать 2.89 Mb.
|
|
M + tm P + tm, где t – доверительный коэффициент. Доверительный коэффициент (t) – это число, показывающее, во сколько раз надо увеличить ошибку средней величины или показателя, чтобы при данном числе наблюдений с желаемой степенью вероятности утверждать, что они не выйдут за полученные таким образом пределы. С увеличением t степень вероятности возрастает. Т.к. известно, что полученная средняя или показатель при повторных наблюдениях, даже при одинаковых условиях, в силу случайных колебаний будут отличаться от предыдущего результат, теорией статистики установлена степень вероятности, с которой можно ожидать, что колебания эти не выйдут за определенные пределы. Так, колебания средней в интервале M+ 1m гарантируют ее точность с вероятностью 68.3% (такая степень вероятности не удовлетворяет исследователей), в интервале M+ 2m – 95.5% (достаточная степень вероятности) и в интервале M+ 3m – 99,7% (большая степень вероятности). Для медико-биологических исследований принята степень вероятности 95% (t = 2), что соответствует доверительному интервалу M+ 2m. Это означает, что практически с полной достоверностью (в 95%) можно утверждать, что полученный средний результат (М) отклоняется от истинного значения не больше, чем на удвоенную (M + 2m) ошибку. Конечный результат любого медико-статистического исследования выражается средней арифметической и ее параметрами: 2. Оценка достоверности относительных величин (показателей). Средняя ошибка показателя также служит для определения пределов его случайных колебаний, т.е. дает представление, в каких пределах может находиться показатель в различных выборках в зависимости от случайных причин. С увеличением численности выборки ошибка уменьшается. Мерой достоверности показателя является его средняя ошибка (m), которая показывает, на сколько результат, полученный при выборочным исследовании, отличается от результата, который был бы получен при изучении всей генеральной совокупности. Средняя ошибка показателя определяется по формуле: р – показатель, q – величина, обратная показателю (100-p, 1000-р и т.д. в зависимости от того, на какое основание рассчитан показатель); n – число наблюдений. 13. Достоверность разности средних и относительных величин: методика вычисления, оценка. В научных исследованиях и клинической практике с целью сравнения двух средних величин или показателей (например, для выявления преимуществ одного метода лечения перед другим, сопоставления результатов исследования в контрольной и экспериментальной группах, сравнения показателей здоровья двух групп населения и т.п.) возникает необходимость не только определить их разность, но и оценить ее достоверность. Разность между двумя средними или относительными величинами (показателями), каждая из которых имеет свою ошибку, также имеет свою ошибку. Средняя ошибка разности (mразн) вычисляется по формуле: Т.о., ошибка разности равняется корню квадратному из суммы квадратов ошибок сравниваемых величин. Мерой достоверности разности двух величин является критерий достоверности (критерий Стьюдента – t): - для средних величин: - для относительных величин: 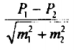 , , где t – критерий достоверности, М1 и М2 - сравниваемые средние, p1 и p2 – сравниваемые показатели, m12 и m22 – их ошибки. Для медико-биологических исследований принято считать, что если критерий достоверности t> 2, то различие двух величин (средних или относительных) следует считать существенным, достоверным, доказанным с вероятностью в 95%. Если t < 2, то различие величин не доказано. 14. Динамические ряды: определение, виды. Цель и способы выравнивания динамических рядов (показать на условном примере). При изучении изменений какого-либо явления во времени составляется динамический ряд. Динамический ряд – это совокупность однородных статистических величин, показывающих изменение какого-либо явления на протяжении определенного промежутка времени. Каждый динамический ряд содержит две составляющие: 1. Периоды времени (годы, месяцы, кварталы, недели) или даты; 2. Величины, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда. Уровни динамического ряда могут быть представлены: - абсолютными величинами; - относительными величинами; - средними величинами. Динамический ряд, уровни которого представлены абсолютными величинами, называется простым динамическим рядом. Динамический ряд, уровни которого представлены относительными или средними величинами, называется сложным или производным. По временной составляющей динамический ряд может быть моментным и интервальным. Моментный динамический ряд состоит из величин, характеризующих явление на какой-то определенный момент – дату (на конец месяца, квартала, года). Например, каждый уровень ряда может характеризовать численность населения, врачей, среднего медицинского персонала на конец какого-либо года. Уровни моментного ряда не могут дробиться. Пример: Моментный динамический ряд (простой, т.е. состоящий из абсолютных величин) Динамика коечного фонда в районе N с 2005 по 2010 гг. (абс. число коек на конец каждого года).
Интервальный динамический ряд состоит из величин, характеризующих явление за какой-то определенный промежуток времени – интервал (неделя, месяц, квартал, год). Например, каждый уровень такого ряда может характеризовать смертность, рождаемость, заболеваемость, среднегодовую занятость койки за какой-то определенный год. Интервальный динамический ряд можно разделить на более дробные периоды или, напротив, укрупить интервалы. Размер интервала исследователь выбирает в зависимости от степени изменчивости явления. Пример: Интервальный динамический ряд (простой, т.е. состоящий из абсолютных величин) Динамика числа родившихся в районе N с 2005 по 2010 гг.
Пример: Интервальный динамический ряд (сложный, т.е. состоящий из относительных величин) Динамика показателей рождаемости в районе N с 2005 по 2010 гг. (интенсивные показатели в %о)
Динамический ряд не всегда состоит из уровней последовательно изменяющихся в сторону снижения или увеличения. Нередко некоторые уровни в динамическом ряду представляют значительные колебания, что затрудняет возможность проследить основную закономерность, свойственную явлению в наблюдаемый период. В этих случаях для выявления общей динамической тенденции рекомендуется произвести выравнивание динамического ряда. Необходимо помнить, что выравнивание уровней динамического ряда нельзя делать механически. Это допустимо только после глубокого и всестороннего анализа причин, обусловивших колебания этих уровней. Механическое выравнивание может искусственно сгладить уровни и завуалировать причинно-следственные связи. Существует несколько методов выравнивания уровней динамического ряда: укрупнение интервала, вычисление групповой средней, вычисление скользящей средней. 1. Укрупнение интервала – производят путем суммирования данных за ряд смежных периодов. Сезонные колебания случаев ОКИ в районе N (по месяцам 2010 г.)
Таким образом, после укрупнения интервалов по кварталам года выявлена определенная тенденция: наибольшее количество заболеваний острыми кишечными инфекциями приходится на летне-осенний период. 2. Групповая средняя – вычисляется как средняя арифметическая уровней, составляющих укрупненный интервал. Пример: Динамика процента расхождения клинических и патологоанатомических диагнозов в больнице города N за 2005-2010 гг.
Уровни динамического ряда, представленные в таблице имеют волнообразные колебания. Выравнивание ряда путем вычисления групповой средней позволило выявить четкую тенденцию к постепенному снижению процента расхождений диагнозов в областной больнице. 3. Скользящая средняя – вычисляется как средняя величина из данного уровня и двух соседних с ним. При этом временной интервал динамического ряда не укрупняется и остается прежним, а значение каждого уровня ряда заменяется на среднюю величину из данного уровня и двух соседних с ним (предыдущего и последующего). Таким образом, данный метод исключает из анализа значения первого и последнего уровней. Пример: Динамика процента расхождений клинического и патологоанатомического диагнозов в больнице города N за 2005-2010 гг.
Ряд, выровненный с помощью скользящей средней, более плавно иллюстрирует общую тенденцию: постепенное уменьшение показателей частоты расхождения диагнозов. 15. Динамические ряды. Показатели динамики изучаемого явления: наименование, методика расчета, сущность (показать на условном примере). Для анализа динамического ряда лучше всего сначала изобразить его графически. Графическое изображение уровней ряда позволяет в наглядной форме обнаружить последовательность изменения изучаемого явления. Динамический ряд можно подвергнуть преобразованиям, целью которых является выявление особенностей изучаемого процесса, а также достижение наглядности в характеристике того или иного явления. Для определения тенденции изучаемого явления рассчитывают следующие показатели динамического ряда: 1. Абсолютный прирост (убыль) – это разность между последующим и предыдущим уровнем (измеряется в тех же единицах, в которых представлены уровни ряда). 2. Темп прироста (убыли) – это отношение абсолютного прироста (убыли) каждого последующего уровня к предыдущему, принятому за 100%. Темп прироста показывает, на сколько процентов увеличился (снизился) последующий уровень по сравнению с предыдущим. Темп прироста = (Абсолютный прирост / Предыдущий уровень) х 100% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
