Лекции Электропривод ГМиММ. 1. Роль электропривода в современных машинных технологиях
 Скачать 3.83 Mb. Скачать 3.83 Mb.
|
|
Тема 2. Лекция 2 2.1. Механические характеристики двигателя и рабочего механизма Назначение электропривода - создавать движение рабочих машин и управлять этим движением. Переменными величинами, характеризующими движение, являются: Таблица 2.1
Изменение величин, характеризующих движение рабочих органов машины, происходит при воздействии на их кинематическую цепь (механическую часть) силF. Для вращательного движения физическим аналогом силы является момент М. Момент создается силой, приложенной к плечу (плечо — кратчайшее расстояние от оси вращения до линии действия силы), например, к радиусу барабана грузоподъемной лебедки (рис.2.1,а); или парой сил, возникающих в электродвигателях вращательного движения (рис.2.1,6) М = FR. 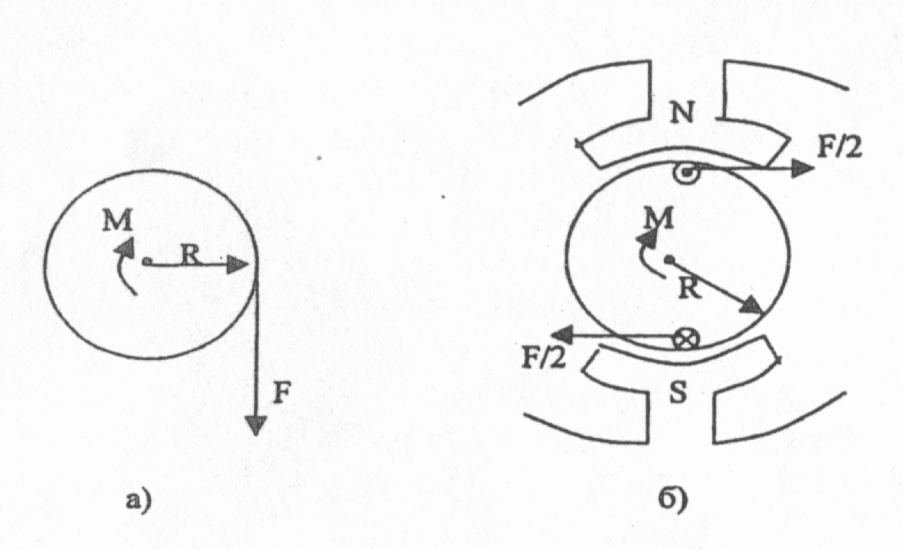 Рис.2.1. Формирование крутящего момента Электрический двигатель вращательного движения является источником момента. Знаки моментов, прикладываемых к механической части электропривода, нужно соотносить со знаком скорости вращения. Одно из направлений вращения вала двигателя (по часовой стрелке «вперед» или против часовой стрелки «назад») условно принимают за положительное направление; противоположное направление — за отрицательное. Соответственно, скорость движения в направлении «вперед» будет иметь знак (+), а скорость движения в направлении «назад» - знак (-). Также поступают при определении знака скорости линейного движения, например линейного двигателя. Момент, развиваемый электродвигателем, может быть положительным, когда двигатель при вращении в положительном направлении работает в двигательном режиме, преобразуя электрическую энергию в механическую, или отрицательным, тормозным (-М), когда двигатель работает в генераторном режиме, преобразуя механическую энергию в электрическую. При изменении направления вращения знаки моментов изменяются на противоположные. Момент двигателя зависит от его скорости. Взаимосвязь момента, развиваемого двигателем, и скорости вращения М = f (ω) определяет механические характеристики электропривода (электродвигателя). Механические характеристики изображаются в поле координат М – ω. Оси координат разделяют поле на четыре квадранта (рис.2.2). В первом квадранте изображаются механические характеристики при работе двигателя в двигательном режиме и положительном направлении скорости его вращения, во втором — при работе в тормозных режимах. В третьем квадранте будут размещаться механические характеристики двигателя при работе в двигательном режиме, но с отрицательным направлением скорости вращения. В четвертом квадранте — механические характеристики двигателя при работе в тормозном режиме и отрицательном направлении скорости вращения. Обычно пользуются представлением механических характеристик в первых двух квадрантах.  Рис.2.2. Поле координат М-о Основным параметром, определяющим вид механической характеристики, является ее жесткость (рис.2.3). 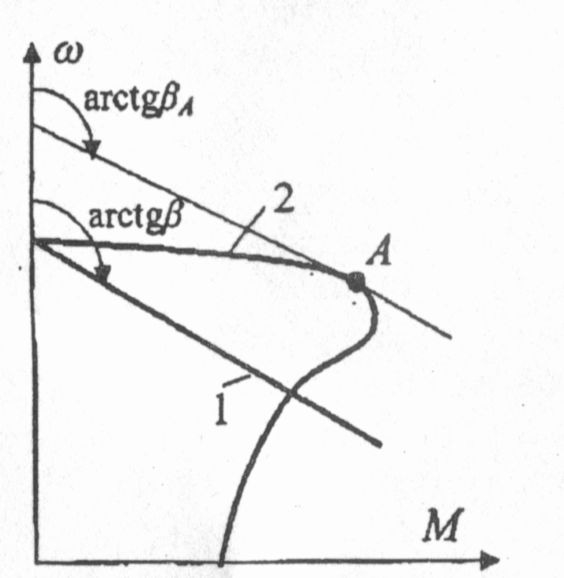 Рис.2.3. К определению жесткости механических характеристик Если механическая характеристика прямолинейна (1), то ее жесткость – величина постоянная и равная тангенсу угла наклона характеристики к оси ординат; если характеристика криволинейна (2), то жесткость определяется тангенсом угла наклона касательной к механической характеристике в данной точке (например, в точке А). Жесткость характеризует способность двигателя воспринимать приложение нагрузки (момента) на его валу. Из (2.1) следует, что Поскольку обычно с увеличением момента нагрузки скорость уменьшается, то жесткость является величиной отрицательной. Если при приложении нагрузки ΔМ скорость Δω уменьшается незначительно, то механическая характеристика считается жесткой. Если при том же значении прикладываемой нагрузки скорость изменяется значительно, то такую характеристику называют мягкой. На рис.2.4 показаны естественные механические характеристики основных видов электродвигателей вращательного движения: 1 — двигателя постоянного тока независимого возбуждения; его механическая характеристика имеет высокую жесткость, постоянную во всех точках; 2 двигателя постоянного тока последовательного возбуждения; жесткость его механической характеристики не постоянна, она мала при малых нагрузках и повышается по мере возрастания момента; З — асинхронного двигателя; его механическая характеристика имеет две явно выраженные части: рабочую - с высокой постоянной отрицательной жесткостью и криволинейную часть с переменной положительной жесткостью; вторая часть характеристики используется только во время пуска двигателя; 4 — синхронного двигателя; он имеет абсолютно жесткую механическую характеристику, параллельную оси абсцисс. 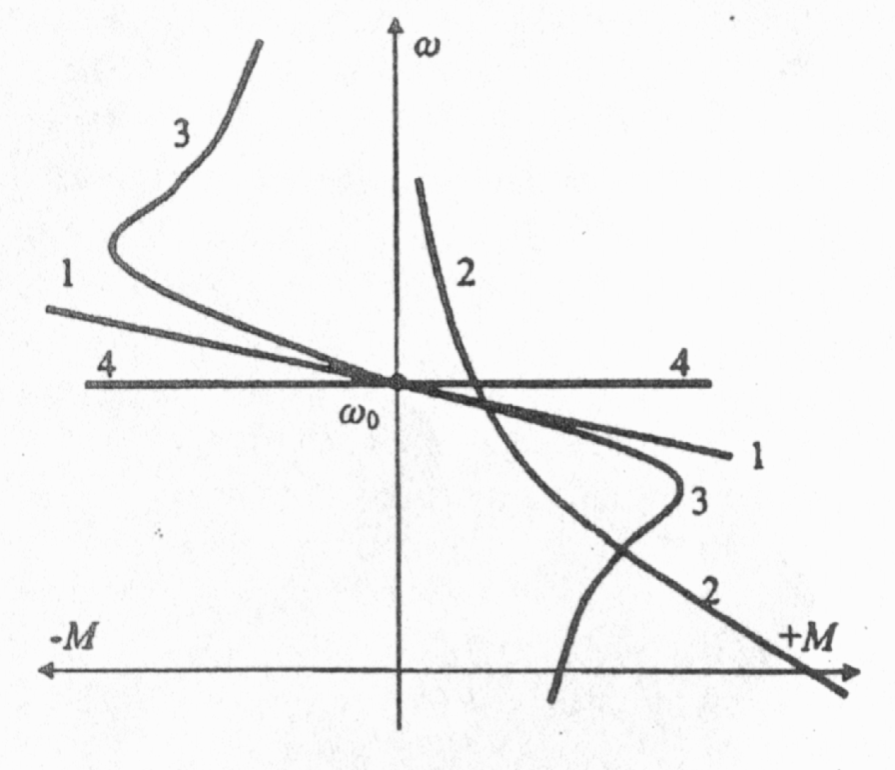 Рис.2.4. Естественные механические характеристики двигателей: 1 - постоянного тока независимого возбуждения; 2 - постоянного тока последовательного возбуждения; З - асинхронного; 4 – синхронного дополнительных элементов. Приведенные на рисунке 2.4. характеристики называют естественными механическ5ими характеристиками. Такие характеристики соответствуют типовой схеме включения, номинальному напряжению и частоте питания и отсутствию в цепях обмоток двигателя дополнительных элементов. Искусственные (или регулировочные) механические характеристики получаются, когда с целью регулирования изменяются параметры питающего напряжения или в цепи обмоток вводятся дополнительные элементы (активные или индуктивные сопротивления, полупроводниковые приборы и др.). Момент сопротивления движению М, создаваемый на рабочем органе машины, также может являться функцией скорости. Зависимость момента сопротивления на валу рабочей машины от скорости М = f (ω) (Мс и ω приведены к валу двигателя) называют механической характеристикой рабочей машины. Ее обычно в I квадранте координатного поля М- ω На рис.2.5 показаны механические характеристики некоторых рабочих машин. Характеристика 1 соответствует машинам с рабочим органом резания; если толщина снимаемого резцом слоя постоянна, то момент сопротивления такой машины не зависит от скорости. Характеристика 2 отвечает условиям работы машин, где момент сопротивления определяется, главным образом, силами трения (транспортеры, конвейеры и др. машины). В этом случае момент сопротивления также не зависит от скорости механизма, однако, при пуске механизма момент, создаваемый силами трения покоя, может существенно превышать момент сил трения при движении. 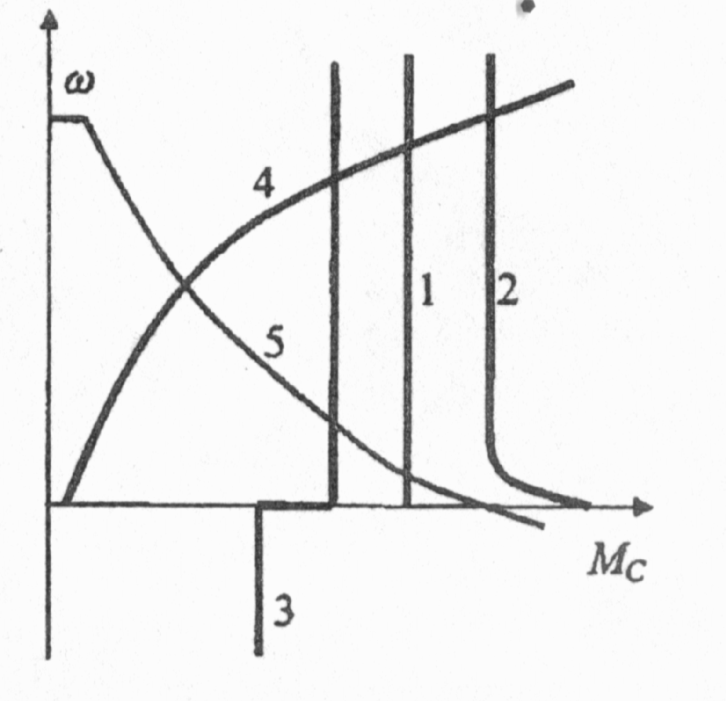 Рис.2.5. Зависимость моментов сопротивления движению от скорости для некоторых рабочих машин Характеристика З относится к грузоподъемным механизмам, где момент сопротивления движению создается, главным образом, силой тяжести. Особенностью данной характеристики является то, что момент при подъеме груза несколько превышает момент сопротивления при спуске груза (характеристика З), что связано с учетом механических потерь в передачах. Для турбомеханизмов (центробежных и осевых насосов, вентиляторов и компрессоров) момент на валу механизма существенно зависит от скорости характеристика 4. Для вентиляторов эта зависимость носит квадратичный характер Мс = Кω2. Характеристикой 5, близкой к гиперболе, обладают намоточные устройства и другие машины, для которых технологически необходима работа с постоянством мощности. Отметим, что моменты на валу рабочей машины, определяемые ее механической характеристикой, не учитывают динамической составляющей момента, которая возникает при изменении скорости двигателя. Вопросы по теме 2.1 1)Что называется коэффициентом жесткости механической характеристики? 2)Двигатели, имеющие абсолютно жесткую механическую характеристику - …; мягкую характеристику - …; жесткую характеристику - … 3)Приведите понятия естественной и искусственной механических характеристик. 2.2. Уравнение движения электропривода К механической системе, совершающий вращательное движение относительно фиксированной оси вращения, прикладываются два момента: момент М, развиваемый двигателем, и момент сопротивления движению М (см. рис.2.7). 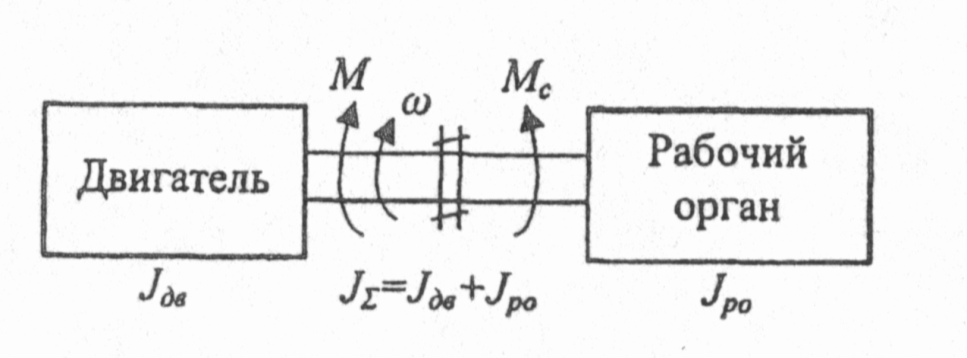 Рис.2.7. Моменты, прикладываемые к механической системе с одной фиксированной осью вращения Если момент, развиваемый электродвигателем, равен моменту сопротивления движению. М = Мс или М – М = 0 (2.1.) то механическая система будет совершать движение с постоянной (установившейся) угловой скоростью или находиться в состоянии покоя (ω=0). Это положение соответствует Первому закону механики Ньютона закону инерции, - который применительно к вращательному движению может быть сформулирован следующим образом: тело, имеющее фиксированную ось вращения, будет находиться в состоянии покоя или равномерного вращения, до тех пор, пока приложенные моменты не выведут его из этого состояния т.е., если алгебраическая сумма моментов, прикладываемых к валу, равна нулю, то механическая система будет вращаться с постоянной скоростью ωуст (или будет в состоянии покоя), т.е. находиться в установившемся режиме. Для поступательного движения условие установившегося режима формулируется как dV / dt = 0, если Момент сопротивления движению обычно называют статическим моментом, т.к. в соответствии с (2.2) он характеризует установившийся режим работы электропривода. 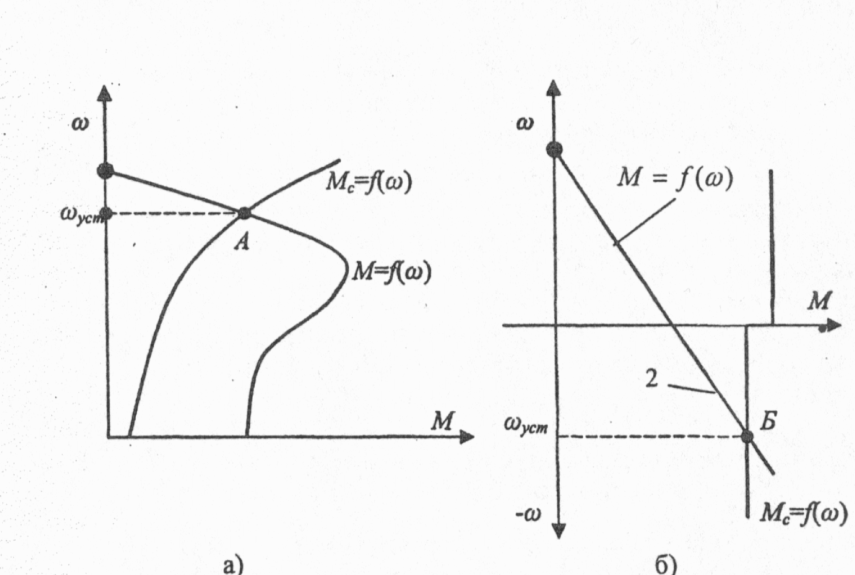  Рис.2.8. Графическое определение скорости установившегося режима движения электропривода Момент двигателя и статический момент зависят от скорости. Найти скорость установившегося режима работы механизма, когда известны механические характеристики двигателя и рабочего механизма, удобно графическим путем. Рис.2.8,а соответствует механической системе, состоящей из вентилятора и асинхронного двигателя. Точка А пересечения механических характеристик двигателя и вентилятора соответствует условию (2.2), т.е. установившемуся режиму работы. На рис.2.8,6 показаны механические характеристики грузоподъемной лебедки, работающей в режиме спуска груза (скорость отрицательна). Для обеспечения постоянной скорости спуска приводный электродвигатель переводится в режим торможения противовключением, которому соответствует механическая характеристика 2. Точка Б пересечения этой характеристики с механической характеристикой лебедки соответствует равенству моментов М=Мс, т.е. установившемуся режиму движения. Статические моменты подразделяют на активные и реактивные. Мса – активный момент сопротивления движению прикладываемый к рабочему органу машины; этот момент создается силами тяжести (например, в грузоподъемных механизмах, лифтах и др.), силами ветра (механизм поворота башенных кранов), и др.; активные моменты могут как препятствовать движению, так и создавать движение, в соответствии с этим знак Мса может быть отрицательным, если его направление противоположно знаку скорости вращения и положительным, если направление момента совпадает с направлением скорости вращения. Мср– реактивный момент сопротивления движению, прикладываемый к рабочему органу машины; этот момент возникает как реакция на движение рабочего органа и всегда препятствует движению (например, момент от сил резания в механизмах главного движения металлорежущих станков, момент от аэродинамических сил вентиляторов и др.); при ω = 0 Мср = 0; к реактивным моментам сопротивления относится также момент от сил трения в подшипниках, передачах и других элементах кинематической цепи рабочей машины; момент трения всегда препятствует движению. Статический момент — полный момент сопротивления движению равен сумме его составляющих Мс = Мса + Мср (2.3.) Знаки всех моментов определяются в отношении знака скорости вращения. Для положительного направления скорости вращения, если момент способствует движению — он положите- лен, если препятствует — отрицателен. Алгебраическая сумма момента двигателя (М) и составляющих статического момента определяет результирующий момент, прикладываемый к валу электродвигателя М∑ = М + Мс (2.4.) М∑ = ± М ± Мса – Мср (2.5.) Для положительного направления движения в формуле (2.5) знак момента М, развиваемого двигателем будет положительным, если он работает в двигательном режиме, и отрицательным, если работает в тормозном режиме. Знак активной составляющей статического момента Мса будет отрицательным, если этот момент препятствует движению (например, подъем груза) и положительным, если этот момент способствует движению (например, спуск груза). С учетом (2.3) М∑ = М – Мс (2.6.) Аналогично для поступательного движения где Если результирующий момент М∑ равен нулю, то механическая система будет находиться в состоянии покоя или равномерного установившегося движения. Если результирующий момент (или результирующая сила) не равен нулю, то происходит изменение скорости механической системы: при положительном значении М∑ (F∑) – ускорение; при отрицательном значении — замедление. Режимы, при которых М∑ ≠ 0, называют переходными или динамическими. Изменение скорости определяется вторым законом Ньютона — законом динамики, согласно которому для поступательного движения — импульс силы равен изменению количества движения Импульс силы — это вектор, равный произведению вектора результирующей силы на время ее действия. Количество движения — это вектор, равный произведению вектора скорости на массу тела. Если масса постоянна, то Этот закон устанавливает, что если результирующая сила не равна нулю, то тело получает ускорение (замедление), величина которого зависит от величины силы и массы. Для вращательного движения относительно фиксированной оси второй закон Ньютона формулируется следующим образом: импульс момента равен изменению количества движения М∑dt = d (Jω) (2.8.) Количество движения — произведение момента инерции вращающихся масс на их угловую скорость. Момент инерции J (кгм2) — параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения J = mR2 Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры. Значения момента инерции для тел вращения приводятся в каталогах и справочниках. Иногда в каталогах дается значение махового момента GD2. Для того, чтобы найти момент инерции нужно GD2 разделить на четыре = GD2/4 Отметим, что механическая инерционность вращающегося тела зависит не только от его массы, но и диаметра. При одной и той же массе тело, имеющее больший диаметр, обладает значительно большим моментом инерции. Поэтому малоинерционные электродвигатели стремятся конструировать с меньшим диаметром ротора большей длины. Напротив, когда в состав кинематической цепи рабочей машины включается маховик, его целесообразно конструировать с большим диаметром. Если момент инерции постоянен, то уравнение второго закона Ньютона можно представить в виде Исходя из того, что М определяет динамику механической системы, то результирующий момент М часто называют динамическим. Учитывая (2.5), получим Это уравнение, отражающее второй закон Ньютона, называют уравнением движения электропривода. Отметим, что в этом уравнении все моменты приложены к валу двигателя, а момент инерции J∑ отражает инерционности всех масс, связанных с валом электродвигателя и совершающих вместе с ним механическое движение. Для поступательного движения уравнение движения электропривода соответственно будет где F – усилие, развиваемое двигателем; Fc – усилие сопротивления движению на штоке этого двигателя; т – массы подвижных элементов, связанные со штоком двигателя; V – линейная скорость штока двигателя. 2.3. Приведенное механическое звено Если рабочий орган машины непосредственно связан с валом электродвигателя, то для анализа движения электромеханической системы: двигатель – рабочий орган, можно пользоваться уравнением (2.1.1). Такая кинематическая схема характерна, например, для вентиляторов, насосов и ряда других машин. Однако во многих случаях рабочий орган машины связан с валом электродвигателя через систему передач: зубчатых, канатных, тексропных и других. В этом случае непосредственное использование уравнения (2.1.1) невозможно, т.к. моменты М и М приложены к разным валам, а инерционные массы вращаются с разными скоростями. Для возможности использования уравнения движения возникает задача приведения всех моментов сопротивления и моментов инерции отдельных кинематических звеньев к одному валу, обычно к валу электродвигателя. Такое приведение является только расчетной операцией. Принцип приведения моментов заключается в сохранении равенства мощностей. Приведение моментов инерции производится на основе принципа сохранения кинетической энергии. 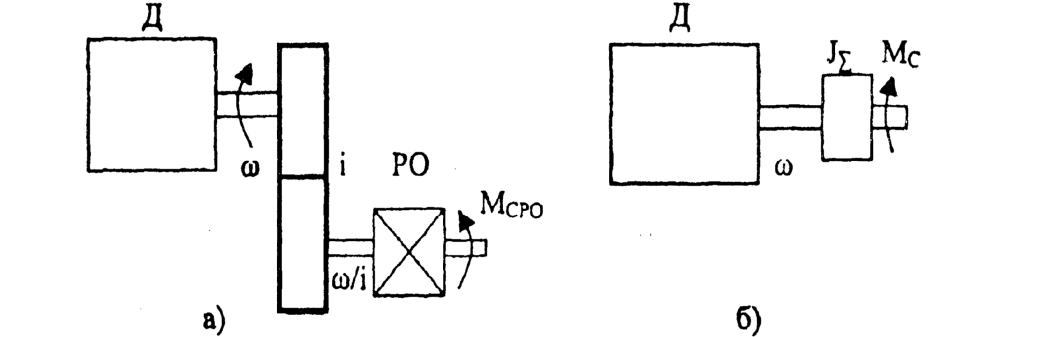 Рис.2.9. Приведение моментов сопротивления и инерции к валу двигателя Если рабочий орган машины (РО) соединяется с валом двигателя (Д) через редуктор с передаточным числом i (см. рис.2.9,а), то для того, чтобы привести момент сопротивления Мс.ро, реально прикладываемый к рабочему органу, к валу двигателя нужно соблюсти условие равенства мощностей Мс.ро · ωро = Мсω (2.13.) Здесь Мс.ро – момент сопротивления движению (далее будем называть его статический момент); ωро – угловая скорость рабочего органа; Мс – момент сопротивления, приведенный к валу электродвигателя; ω – скорость вала двигателя. Если учитывать потери в редукторе, то в уравнение (2.13) вводится кпд передачи ηред. Мс.ро · ωро = Мсωηред Следовательно, если известен статический момент на валу рабочего органа, статический момент, приведенный к валу двигателя, находится по формуле: Общее правило — для того, чтобы привести статический момент к валу двигателя нужно реальный статический момент на валу рабочего органа разделить на передаточное число и кпд передачи. Для приведения момента инерции рабочего органа J к валу двигателя нужно соблюсти равенство кинетических энергий Следовательно, приведенный к валу двигателя момент инерции рабочего органа находится по формуле: Общее правило — для того, чтобы привести момент инерции к валу двигателя нужно реальный момент инерции кинематического звена разделить на квадрат передаточного отношения. В результате приведения статического момента и момента инерции к валу двигателя вместо реальной кинематической схемы получаем расчетную (рис.2.9,6), на основании которой можно пользоваться уравнением движения электропривода. В некоторых кинематических схемах рабочих машин присутствуют звенья с поступательным движением. Рассмотрим такой случай на примере кинематической схемы грузоподъемной лебедки (рис.2.10). Статический момент (активный) создается силой тяжести груза на крюке лебедки G = mгр · g Этот момент прикладывается к валу барабана лебедки и равен Мс (бар) = мгрgRбар Для того чтобы привести статический момент к валу двигателя, для случая подъема груза нужно воспользоваться формулой (2.14): 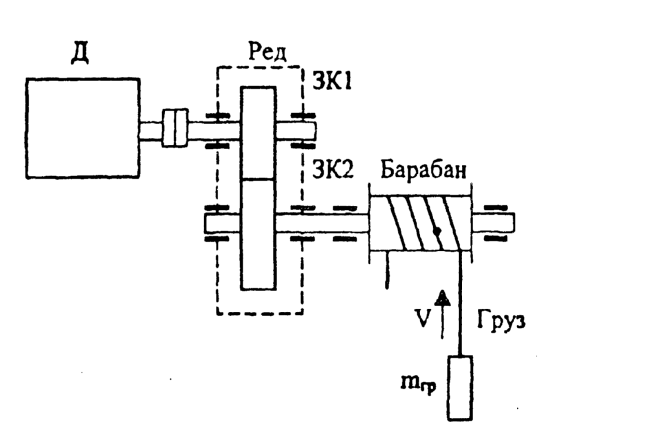 Рис.2.10. Кинематаческая схема грузоподъемной лебедки Особенность данного случая при наличии активного статического момента состоит в том, что приведенный статический момент для режимов подъема и спуска груза будет различным. При подъеме груза двигатель должен преодолевать сопротивление трения (потери мощности) в редукторе и других элементах, поэтому приведенный к валу двигателя статический момент будет несколько больше, что учитывается делением на кпд передачи. При спуске груза, когда движение механической системы совершается под действием активного статического момента, приведенный к валу двигателя момент будет несколько меньше, так как силы трения действуют согласно с тормозным моментом двигателя. Поэтому при спуске груза кпд передачи следует вводить в числитель формулы (2.14): Следует заметить, что эта особенность проявляется только в случае приведения активного статического момента. Для нахождения суммарного момента инерции механической системы воспользуемся формулой (2.15) для приведения вращающихся масс и принципом равенства кинетических энергий для приведения поступательно движущейся массы т. Здесь J – момент инерции массы т, линейно движущейся со скоростью V, приведенный к вращательному движению со скоростью вала двигателя ω. Так как V = ωбарRбар, то Суммарный приведенный к валу двигателя момент инерции рассматриваемой системы (рис.2.9) будет: где Jрот, Jбар, Jзк1, Jзк2 – моменты инерции соответствующих механических звеньев. Уравнение движения электропривода для режима подъема груза будет: 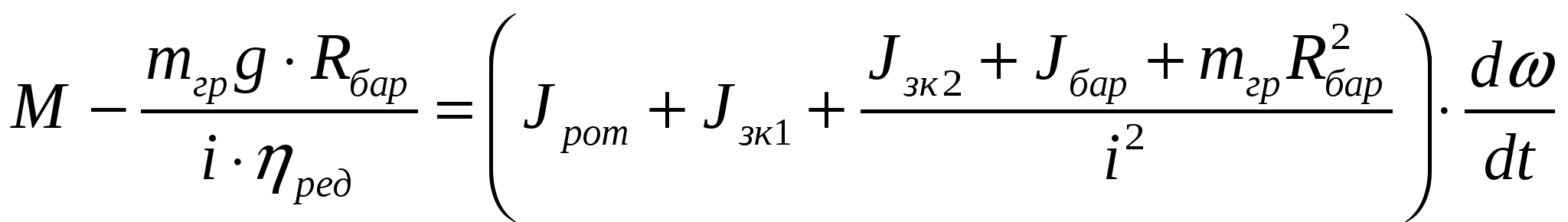 Механическая часть электропривода включает в себя: ротор (якорь) электродвигателя, рабочий орган машины и систему механических передач и трансмиссий. Если все элементы механической части во всех движениях имеют равную или пропорциональную скорость (вращения или линейную), то такая механическая система может рассматриваться как жесткая. В этом случае, пользуясь формулами приведения параметров к валу двигателя, можно рассматривать систему как жесткое механическое звено с суммарным приведенным моментом инерции J∑ и для анализа ее динамических характеристик пользоваться уравнением движения электропривода (2.11). Такую механическую систему называют одномассовой. Во многих случаях кинематическая схема рабочей машины содержит упругие элементы: торсионы, длинные валы, упругие муфты, тексропные, канатные передачи и др. В реальных схемах иногда приходится учитывать люфты и зазоры в зубчатых передачах и соединениях. В этих случаях кинематическую схему рабочей машины нельзя рассматривать как жесткую одномассовую систему. В особенности это касается высокоточных электроприводов и рабочих машин, работающих в интенсивном динамическом режиме. В этом случае математическое описание процессов движения таких систем, называемых многомассовыми, существенно усложняется, И их анализ целесообразно проводить с использованием компьютерного моделирования. Вопросы по лекции 2: 1)В каких режимах в зависимости от направления момента и скорости вращения может работать эл.двигатель? 2)Параметр характеризующий механическую характеристику это - … 3)Момент инерции системы ЭП зависит от … 4) Динамический момент опрделяется … 5)Приведение моментов статического сопротивления к валу двигателя выполняют с учетом … Лекция №3 | ||||||||||||||||||||||||||||||||||||||||||
