Урусова Я.А._Мм-1401. Формирование критического мышления при обучении математике учащихся общеобразовательной школы

• Название: Формирование критического мышления при обучении математике учащихся общеобразовательной школы
• Дата: 08.04.2023
• Размер: 280.63 Kb.
• Имя файла: Урусова Я.А._Мм-1401.docx
• Тип: Документы; #1046199
• страница: 10 из 13

балл - попытка выполнения задания, но имеются ошибки в решении;

балла - задание выполнено с полным развёрнутым решением.

Отметка «5» - 7-8 баллов;

Отметка «4» - 5-6 баллов;

Отметка «3» - 4-3 баллов;

Отметка «2» - меньше 3 баллов.

Ответы к заданиям:

Вариант 1: 1) 10. 2) 0. 3) 22. 4) 128.

Вариант 2: 1) 6. 2) 0,4. 3) 13. 4) 243.


§ 7. Методические материалы на формирование критичности мышления
учащихся при изучении темы «Логарифмическая функция»

Выявив методические особенности формирования критичности мышления учащихся общеобразовательной школы с помощью задач, были разработаны соответствующие методические материалы: самостоятельная работа, математический диктант, тест, кроссворд.

Самостоятельная работа на тему «Логарифмическая функция»

Работа составлена в 2-х вариантах на основе заданий с сайта «Решу ЕГЭ» [52]. Задания направлены на формирование различных умений.

1 вариант:

1. 
   Найдите наименьшее значение функции у = 3х — ln(% + 3)3 на отрезке [- 2,5; 0]. Оцените правильность решения.
   
2. 
   Найдите ошибки в рассуждениях при решении задания:
   

Опишите свойства логарифмической функции у = 1од_ах, при а > 1:


61

D (f)= (0, + a>); не является ни четной, ни нечётной; не ограничена сверху, ограничена снизу; не имеет ни наибольшего, ни наименьшего значений; непрерывна; E(f) = (- ю; + ю); выпукла вверх. Найдите точку максимума функции у = ln(% + 5) — 2х + 9 . Сравните два алгоритма нахождения максимума функции (Табл.8), найдите в них ошибки или пропущенные этапы решения, если они есть. Проведите обобщение данных алгоритмов и составьте свой алгоритм нахождения максимума функции. Таблица 8 Алгоритм 1

Алгоритм 2

1.Найдите производную заданной функции. 2.Определите нули функции. 3. Найдите значения функции.

.Находим область определения функции. .Ищем критические точки. З.Определяем знаки производной в полученных промежутках.

4. 
   Найдите наименьшее значение функции у = log₄(x² + 6х + 25) — 5 . Опровергните предложенное решение:
   

Решение: Квадратный трехчлен у = ах² + Ьх + с с положительным старшим коэффициентом достигает наименьшего значения в точке х = — ^, в нашем случае - в точке - 3. Функция у = log₄(x² + 6х + 25) — 5 в этой точке определена и принимает значение Zog₄((—3)² + 6 * (—3) + 25) — 5 =

Zog₄16 — 5 = 4 — 5 = —1. Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции. Ответ: - 1.

2 вариант:

1. 
   Найдите наименьшее значение функции у = 10% — ln (х + 10)10 на
   

62

отрезке [- 9,5; 0]. Оцените правильность решения. Найдите ошибки в рассуждениях при решении задания: Опишите свойства логарифмической функции у = 1одах, при 0< а < 1: D (f)= (0, + да); является четной; убывает на (0, + да); не ограничена сверху, не ограничена снизу; непрерывна; E(f) = (- да; + да); выпукла вниз. Найдите точку минимума функции у = 2х — ln(% + 3) + 7 . Сравните два алгоритма (Табл.9), найдите в них ошибки или пропущенные этапы решения, если они есть. Проведите обобщение данных алгоритмов и составьте свой алгоритм нахождения максимума функции. Таблица 9 Алгоритм 1

Алгоритм 2

1.Найдите производную заданной функции. 2.Определите нули функции. З.Найдите значения функции.

.Находим область определения функции. .Ищем критические точки. З.Определяем знаки производной в полученных промежутках.

4. 
   Найдите наименьшее значение функции у= 1од5(х² + 4х + 29) — 8. Опровергните предложенное решение:
   

Решение: Квадратный трехчлен у = ах² + Ьх + с с положительным старшим коэффициентом достигает наименьшего значения в точке х = — ^, в нашем случае - в точке -2. Функция у= 1од5(х² + 4х + 29) — 8 в этой точке определена и принимает значение 1од5((—2')² + 4 * (—2) + 29) — 8 =

1од525 — 8 = 5 — 8 = —3. Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции. Ответ: - 3.


63





Данную самостоятельную работу можно использовать после изучения темы «Логарифмическая функция» для проверки остаточных знаний учащихся и подготовки к ЕГЭ, а так же для проверки уровня развития критичности мышления. Ответы и решения данной самостоятельной работы можно увидеть в Приложение 2.

Математический диктант на тему «Логарифмическая функция».

Математический диктант составлен на основе анализа методической литературы [40; 41] с использованием заданий типа «вопрос-ответ». Его можно использовать после ознакомления учащихся с новым материалом. При организации обучения с использованием данного диктанта учитель читает вопросы, учащиеся отвечают письменно на листочках либо «да», либо «нет», комментируя ответ.

Вопросы:

1. 
   Логарифмическая функция у = 1од_ах определена при любом х ?
   
2. 
   Правда, что функция у = 1од_ах определена при a > 0, a / 1, x > 0?
   
3. 
   Областью значений логарифмической функции является множество действительных чисел?
   
4. 
   Верно ли утверждение, что логарифмическая функция не является ни четной, ни нечетной?
   
5. 
   Областью определения логарифмической функции является множество действительных чисел?
   
6. 
   Верно ли, что ось у является вертикальной асимптотой графика логарифмической функции?
   
7. 
   Ответьте, функция у = 1од3х - убывающая?
   
8. 
   Логарифмическая функция у = 1од_ах имеет экстремум в точке (1;0)?
   
9. 
   Скажите, график логарифмической функции у = 1од_ах проходит через точку с координатами (1;0)?
   
10. 
    График логарифмической функции у = 1од_ах находится в 1 и 4 четвертях?
    
11. 
    Скажите, существует логарифм отрицательного числа?
    

64

12. 
    Вся числовая прямая это область определения логарифмической функции, а промежуток (0; + да) является областью значений этой функции?
    
13. 
    Правда ли, что монотонность логарифмической функции зависит от основания логарифма?
    
14. 
    Верно ли, что график логарифмической функции у = log_ax проходит через точку (0;0)?
    

Ответы: 1) нет; 2) да; 3) да; 4) да; 5) нет; 6) да; 7) нет; 8) да; 9) да; 10) да; 11)нет; 12) нет; 13) да; 14) нет.

Тест на тему «Логарифмическая функция».

Тест составлен на основе анализа методической литературы [40; 41]. В нем используются задания на умение эффективно осуществлять отбор полезной информации, содержащейся в самой задаче, в процессе решения и его результатах. Его можно использовать после изучения темы для проверки остаточных знаний у учеников.

Вариант 1:

1. 
   На каком рисунке (рис.6) схематично изображен график функции у =
   

1од5Х?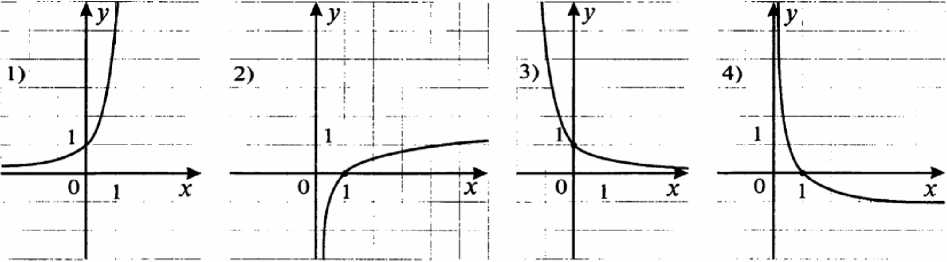





Рис. 6

2. 
   Для функции у = logyx выберите верное утверждение:
   

4

1. 
   Областью значений функции является множество положительных чисел.
   
2. 
   Функция является четной.
   

65

3. 
   Функция убывает.
   
4. 
   Графиком функции является гипербола.
   

3. 
   Областью определения функции у = 1од0,1(3 — 2х) является
   

множество:

1. 
   (- ю; + ю). 2.(- ю; 2). 3. (- ю; 1,5]. 4.(- ю; 1,5).
   

4. 
   Какому промежутку принадлежит корень уравнения log7(2x — 20) = log₇ 4.
   

1. 
   (- ю; 3). 2. ( - ю; 12). 3. ( 11; 14) . 4. [0 ; 2 ].
   

5. 
   Найдите область определения функции lg(x + 7)
   

1. 
   (- 7; 0). 2. [- 7; +ю). 3. (7; +ю). 4. (- 7; +ю).
   

6. 
   Какая функция является убывающей?
   

1. 
   у = log5 х . 2. у = logio х . 3. у = log₁₃x . 4. у = logo,8 х .
   

3

7. 
   Какова область значений функции у = 31од₂х — 4?
   

1. (0;+а>). 2. (-а>; +а>). 3. [-4; 3]. 4. [-4; +х>).

8. 
   График какой функции изображен на Рис.7?
   

9. 
   y = log3 (x + 2).
   
10. 
    y = log3 (x -