Урусова Я.А._Мм-1401. Формирование критического мышления при обучении математике учащихся общеобразовательной школы

• Название: Формирование критического мышления при обучении математике учащихся общеобразовательной школы
• Дата: 08.04.2023
• Размер: 280.63 Kb.
• Имя файла: Урусова Я.А._Мм-1401.docx
• Тип: Документы; #1046199
• страница: 11 из 13

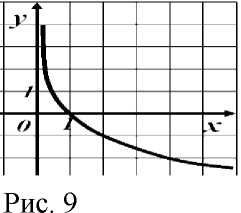
2).

y = log3 (2 - x).

у = 1од2(х + 2).





Рис. 7

9. 
   Какая из представленных функций является убывающей?
   

1. у=2^х . 2. у= log1,15 х. 3. у= log0, 5 х.

Вариант 2:

1. 
   На каком рисунке (рис.8) схематично изображен график функции у = logix ?
   

2


66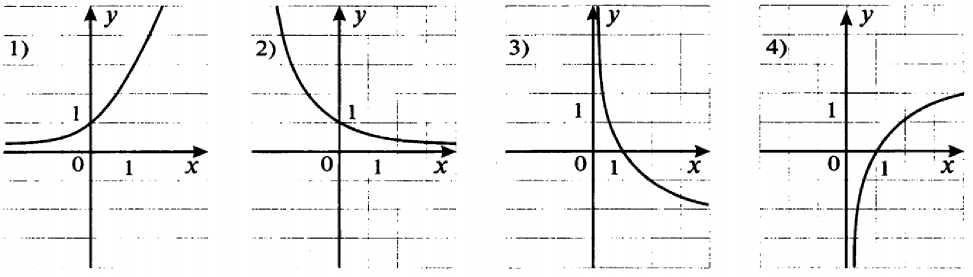








Рис.8

2. 
   Для функции у = 1од5х выберите верное утверждение:
   

1. 
   Областью значений функции является множество всех действительных чисел.
   
2. 
   Функция возрастает на R.
   
3. 
   Функция является нечетной.
   
4. 
   График функции проходит через точку (1;0).
   

3. 
   Областью определения функции у = 1д(1 — 4х) является множество:
   

1. 
   (- /; + /). 2. (0,25; + /). 3. (- /; 0,25). 4. (- /; 0,25].
   

4. 
   Какому промежутку принадлежит корень уравнения log2⁽X — 10) = log2 3.
   

1. 
   (- /; 8). 2. (12; + /). 3. (11; 13). 4. [15; 18].
   

5. 
   Найдите область определения функции lg(x — 4)
   

1. 
   [4; +/). 2. (- 4; +/). 3. (0; 4). 4. (4; +/).
   

6. 
   Какая функция является возрастающей?
   

1. 
   у = logo,5 х . 2. у = log1x. 3. у = log₁₃x . 4. у = log4x.
   

7. 
   Какова область значений функции у = 5 — 21пх?
   

1. 
   (0;5). 2. [5; +да). 3. [-2; 5]. 4. (-да; +да).
   

2. 
   График какой функции изображен на Рис.9?
   

1. У =





67

У = log2 x. У = logo,2 x . У = logi x. 2 Какая из представленных функций является убывающей? y = log1,1 х. у = - log0, 5 х. у = log5 х. 4 y = log0,2x. Ответы: Вариант 1 вопрос	1	2	3	4	5	6	7	8	9
ответ	2	3	4	3	4	4	2	1	3

Вариант 2 вопрос	1	2	3	4	5	6	7	8	9
ответ	3	4	3	2	4	3	4	4	4

Математический кроссворд на темУ «Логарифмическая фУнкция»

Математический кроссворд составлен на основе анализа методической литературы [40; 41]. Кроссворд направлен на формирование таких умений, как: критично подходить к полученной информации. Его можно использовать после изучения темы для проверки остаточных знаний у учеников, которые должны его заполнить (см. Рис.10).

Вопросы по горизонтали:

1. 
   Логарифм с основанием равным числу е?
   
2. 
   Назовите свойство, характерное для логарифмической функции с основанием, а>1?
   
3. 
   Что в логарифмической функции не зависит от основания логарифма?
   

68

Верно, что логарифмическая функция не является ни четной, ни нечетной? Логарифм с основанием 10? Чему равен логарифм 1од2128? Вопросы по вертикали: Действие нахождения логарифма числа (выражения)? Чему равен логарифм единицы? Множество точек, координаты которых удовлетворяют некоторому отношению. Как ведет себя график функции при 0 Графики показательной и логарифмической функций относительно прямой у=х ...? Что есть в каждом уравнении, слове и растении?					1		2
												3
1
									4
														6
								3
		2					5
											6
				4
	5

Рис. 10


69



Ответы по горизонтали: 1. Натуральный. 2. Возрастание. 3. Выпуклость.

4.Да. 5. Десятичный. 6. Семь.

Ответы по вертикали: 1. Логарифмирование. 2. Ноль. 3. График. 4.Убывает. 5. Симметричны. 6. Корень.

Все вышерассмотренные методические материалы способствуют формированию критичности мышления учащихся общеобразовательной школы при обучении математике.

§ 8. Результаты констатирующего эксперимента

В ходе прохождения преддипломной практики мною проводился констатирующий педагогический эксперимент, который включал:

1) анкетирование учителей математики с целью выявления фактического уровня владения ими методикой формирования критического мышления учащихся общеобразовательных школ на уроках;

2) проведение диагностической контрольной работы с целью выявления у учащихся фактического уровня сформированности критического мышления.

Анкетирование учителей математики проводилось на базе МБУ «Школа № 80» и МБУ «Школа № 7» г.о. Тольятти (10 человек) в апреле 2016 года. Текст анкеты представлен в Приложение 3. Анкета включала семь вопросов.

При выборе определения понятия критического мышления 60% учителей математики указали что, критическим мышлением понимают специфическую форму оценочной деятельности учащихся, направленную на выявление степени соответствия (или несоответствия) того или иного продукта принятым эталонам и стандартам.

При ответе на второй вопрос о том, почему современный школьник должен владеть навыками критического мышления, 60% учителей отметили, что критическое мышление помогает оптимизировать учебный процесс и улучшить качество усвоения материала.


70



70% опрошенных учителей математики, при ответе на третий вопрос, какими умениями должен обладать ученик при обучении в общеобразовательной школе, чтобы мыслить критически, выделяют умение эффективно осуществлять отбор полезной информации, содержащейся в самой задаче, процессе решения и его результатах.

На четвертый вопрос о том, какие из приемов развития критического мышления Вы знаете, 80% учителей математики выбирают прием «мозговой штурм».

При ответе на пятый вопрос о том, какие из приемов развития критического мышления Вы используете на уроке, в каком классе, 70% учителей выбрали прием «мозговой штурм», который применяют в основном в 5-6 классах. Так же 50% опрошенных учителей математики выделяют прием «инсерт» и используют его в 10 - 11 классах.

На шестой вопрос о том, по какой причине вы не используете остальные приемы развития критического мышления, 60% учителей считают их неэффективными при обучении математике учащихся.

Все опрошенные учителя математики, при ответе на седьмой вопрос, указали все формы реализации технологии развития критического мышления учащихся на уроках, такие как: дискуссия, 8-9 классы; лекция, 10-11 классы; семинар, 10-11 классы; конференция, 10-11 классы; исследование, 5-6 и 9-11 классы.

Диагностическая контрольная работа проводилась среди учащихся 11 класса МБУ «Школа № 80» г.о. Тольятти в мае 2016 года.

В эксперименте приняло участие 20 учеников 11 класса, им была дана самостоятельная работа на тему «Логарифмическая функция», время для ее выполнения - один урок, текст работы изложен в §7, результаты показаны в Таблице 10.

Эксперимент показал, что большинство учащихся справились с подобранными заданиями, значит критичность мышления у них развита.


71

Таблица 10 Анализ результатов самостоятельной работы Кол-во учеников: 20	Номер задания
Тема: Логарифмическая функция	1	2	3	4
Правильно и полностью выполнили задание	17	15	13	15
Неправильно выполнили задание	3	5	7	5
% от общего числа учащихся, выполнивших задание	85%	75%	65%	75%

Таким образом, в результате анкетирования учителей математики установлено, что учителя понимают, что критическое мышление помогает оптимизировать учебный процесс и улучшить качество усвоения материала учащимися; 70% из них используют в основном в 5-6 классах прием мозгового штурма; 50% учителей в 10 - 11 классах выделяют прием

«инсерт», другие приемы формирования критического мышления они считают неэффективными при обучении математике учащихся. Технология развития критического мышления еще недостаточно распространена и мало используется в практической деятельности учителей.


72



ВЫВОДЫ ПО ВТОРОЙ ГЛАВЕ

1. 
   Выполнен анализ школьных учебников и программы по алгебре и началам анализа для общеобразовательных школ (профильный уровень). Установлено, что по теме «Логарифмические уравнения» в учебнике Н.Я Виленкина отводится 1 задание на развитие критичности мышления учащихся, в учебнике А.Г. Мордковича - 14 заданий, в учебнике М.Я. Пратусевича - 6 заданий; по теме «Логарифмическая функция» в учебнике Н.Я. Виленкина - 12 заданий, в учебнике А.Г. Мордковича - 11 заданий, в учебниках М.Я. Пратусевича и Г.К. Муравина - по 3 задания.
   
2. 
   Разработаны задания по темам «Отбор корней при
   

решении логарифмических уравнений» (с применением кейс - технологии), «Логарифмическая функция» на формирование критичности мышления учащихся и соответствующие методические рекомендации по их применению.

3. 
   Проведено анкетирование учителей математики в МБУ «Школа №80» и «Школа №7» г.о. Тольятти с целью выявления фактического уровня владения ими методикой формирования критического мышления учащихся общеобразовательных школ на уроках.
   
4. 
   Проведена диагностическая контрольная работа в 11 классе МБУ «Школа №80» г.о. Тольятти с целью выявления у учащихся фактического уровня сформированности критического мышления. Результаты эксперимента показали, что у учащихся развита критичность мышления, о чем свидетельствует большой процент верных решений задач.
   

73