Методы интерполяции и аппроксимации

• Название: Методы интерполяции и аппроксимации
• Дата: 31.01.2022
• Размер: 93.46 Kb.
• Имя файла: Interp_app.docx
• Тип: Документы; #347959
• страница: 11 из 13

Метод наименьших квадратов

Суть метода наименьших квадратов заключается в нахождении таких значений х_i, при которых сумма квадратов отклонений (ошибок) e_i=y_i– f_i(x) будет стремиться к минимуму

2
n


e
_{ i} 

n

_( y_i
f(x_i
))²  min . (9)

i1

i1 ^x

Т.к. каждое значение x_iв общем случае «сопровождается» соответствующим коэффициентом а_i(i = 0, 1, 2, …, n), то задача сводится к нахождению данных коэффициентов. Введем обозначение функции

n

F(a, a, ...,a)  _( y f(x))².

(10)

0 1 n i ii1

Тогда, на основе обращения в точке минимума функции F в нуль ее производных, для определения вышеупомянутых коэффициентов составляется нормальная система:

_ dF



^da₀

 <sup>dF

</sup>da

 0;
 0;

^ 1

^...



_ dF

^_da_n

 0.

Существенным недостатком метода является громоздкость вычислений, вследствие чего к нему прибегают при достаточно точных экспериментальных данных при необходимости получения очень точных значений функции.

2. Линейная аппроксимация

В ряде экспериментов данные распределяются таким образом, что оказывается возможным описать их изменение линейной зависимостью (линейным уравнением) (рис. 7)

P(x)=ax+b. (11)

Формулы для расчета коэффициентов aи bопределяются по методу наименьших квадратов (9), подставив (11) в (10)

n

F _( y_i

i1

• 
  a x_i
  

 b)²  min . (12)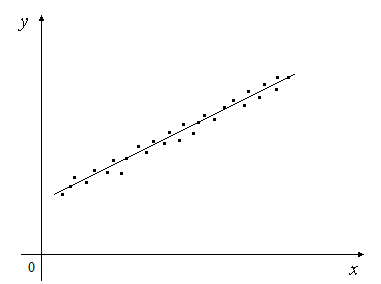

Рис. 7. Линейная аппроксимация

Для решения (12) составляется система из двух уравнений с двумя неизвестными

_ dF

^ da

^ dF

 0;

(13)

^  0.

^ db

Подставляя в (13) формулу (12), получаем

^ dF

n

 2  ( y

• 
  a x
  

 b) 1  0,

^ db



^ i i

i1
(14)

_dF

^_ da

 2 

n

_( y_i

i1

и

• 
  a x_i
  
• 
  b)  x_i
  

 0.

^an x²  bn x

n

 (x
 y)

 ^ i

^ i1

 _n

 _i

i1

n

 _i

i1

i

, (15)


^a_ x_i

• 
  nb _ y_i
  

 i1

i1

Решая полученную систему (15) методом подстановки, получаем формулы для нахождения коэффициентов aи b:

n n n

n _(x_i y_i)  _ x_i _ y<sub>i

a</sub>i1 i1 i1 _{, (16)}

n _ n _²

n _ x²  ^ _ x^

i

i1

i

 i1 

n n

y a x

n n

y x² 

n n

x (x

 y)

 _i _i

 _i _i

^ i ^ i i

_b i1 i1 _ i1 i1 i1 i1 _{. (17)}

ⁿ n _ n _²

n _ x²  ^ _ x^