Методы интерполяции и аппроксимации

• Название: Методы интерполяции и аппроксимации
• Дата: 31.01.2022
• Размер: 93.46 Kb.
• Имя файла: Interp_app.docx
• Тип: Документы; #347959
• страница: 10 из 13

2. Аппроксимация функций

Аппроксимация – замена одних математических объектов другими, в том или ином смысле близкими к исходным.

При интерполировании интерполирующая функция строго проходит через узловые точки таблицы вследствие того, что количество коэффициентов в интерполирующей функции равно количеству табличных значений.

Аппроксимация – метод приближения, при котором для нахождения дополнительных значений, отличных от табличных данных, приближенная функция проходит не через узлы интерполяции, а между ними (рис. 4).

7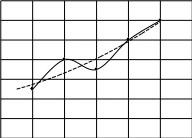
y

6

5

4

3

2

1

0


6
0 1 2 3 4 5 _x

• 
  интерполирующая функция
  
• 
  аппроксимирующая функция
  

Рис. 4. Вид интерполирующей и аппроксимирующей функций

Если аналитическое выражение функции, описывающей закон изменение y_i(i=1, 2,…, n) неизвестно или весьма сложно, то возникает задача найти такую эмпирическую формулу

^{f y(х)},

значения которой при x=x_iмало отличались бы от опытных данных.

Геометрически задача построения функции f(x) по эмпирической формуле состоит в проведении усредненной кривой – кривой, проходящей через середину области значений (табл. 8) (рис. 5).

Таблица 8

Экспериментальные данные

x	1	2	3	4	5
y	2,5	4	3,5	5	5,5

6
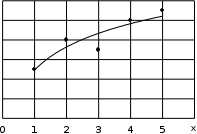y

5

4

3

2

1


6
0
Рис. 5. Пример аппроксимирующей функции

Интерполяцией данные описываются более точно, чем при аппроксимации, но в ряде случаев обосновано применение аппроксимации:

• 
  при значительном количестве табличных данных (интерполирующая функция становится громоздкой);
  
• 
  интерполирующей функцией невозможно описать данные при повторении эксперимента в одних тех же начальных условиях (требуется статистическая обработка;
  
• 
  для сглаживания погрешностей эксперимента. Данные x_iи y_iобычно содержат ошибки, поэтому интерполяционная формула повторяет эти ошибки. Из рисунка (рис. 6) видно, что значения yпостоянно и равномерно увеличивается при росте x, а разброс данных относительно аппроксимирующей функции можно объяснить погрешностью эксперимента.
  

5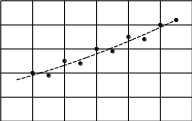
y
4
3
2
1
0


6
0 1 2 3 4 5 _x

Рис. 6. Пример построения аппроксимирующей функции

При построении аппроксимирующей зависимости определяют:

• 
  аналитический характер эмпирической формулы. Предпочтение отдается простым формулам, обладающим хорошей точностью;
  
• 
  наилучшие параметры эмпирической зависимости.
  

Существует несколько методов аппроксимации, рассмотрим некоторые из них.