Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
Комплекснаядиагностическаяработа поалгебреиначаламанализа10класс2021-2022 учебныйгод авторы: Маркель Татьяна Петровна, Северо-Казахстанская область, районМ.Жумабаева,КГУ«Таманскийкомплекс школа-ясли-сад»,педагог-эксперт ЖуменкоСветланаНиколаевна,Алматинскаяобл.,г.Талдыкорган,КГУСШГ16,учительвысшей категории Продолжительность – 45 минут Типы заданий: МВО – задания с множественным выбором ответов; РО – задания, требующие развернутого ответа Характеристиказаданий
Вариант 1 Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. х2 ху 36 1.3. Решите систему уравнений ху у2 45 A) (4;-5); (-4;5) B) (-4;-5); (-4;5) C) (4;5); (-4;5) D) (4;5); (-4;-5) Второй член арифметической прогрессии равен 9, а ее третий член больше первого на 12. Найдите сумму десяти первых членов прогрессии. A) 280 B) 300 C) 320 D) 310 Найдите числовое значение выражения: 2 B) 3,5 C) 2,5 D) 3 3sin 6 2 cos ctg2 6 Найдите наименьший положительный период функции y sin 2x cos2x 2 2 4 На каком из рисунков изображено решение системы неравенств A) 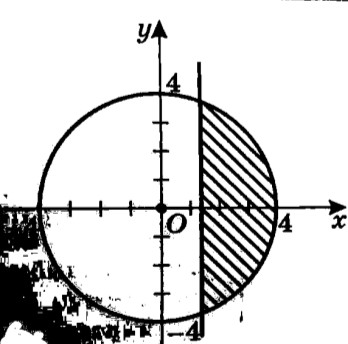 B) B) 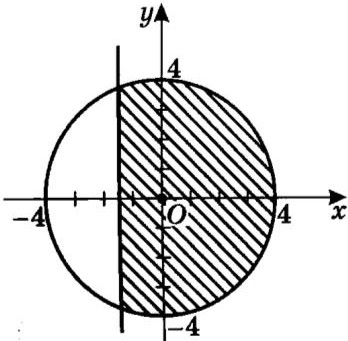 C) 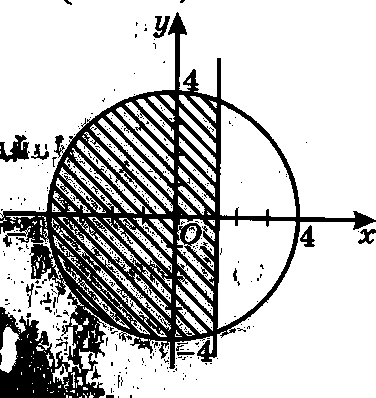 D) D) 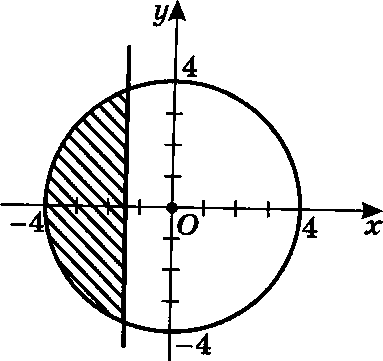 x2 y2 16 x 1,5 Вычислите tg, если sin5 ; . 5 12 13 2 5 12 12 5 D) 12 5 Представьте бесконечную периодическую дробь 1,2(6) в виде обыкновенной дроби. 1 1 15 1 2 15 1 1 5 1 4 15 Упростите выражение 1 cos sin 2 0 cos2 - 1 sin2 Задания уровня В Двое рабочих могут закончить определенную работу за 12 дней. После 8-дневной совместной работы один из ни заболел. Второй рабочий закончил оставшуюся работу за 5 дней. Сколько дней понадобится каждому работнику, чтобы выполнить работу по отдельности? Докажите тождество sin3sin cos3 cos tg2 Определите число членов геометрической прогрессии, если известно, что, если b3 b1 8, b6 b4 216, Sn 121 Вариант 2 Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. х2 ху 6 1.4. Решите систему уравнений ху у2 10 A) (1,5;- 2,5); (-1,5;5,5) B) (- 1,5;2,5); (-1,5;5,5) C) (1,5;2,5); (-1,5;5,5) D) (1,5;2,5); (1,5; - 5,5) Сумма первого и третьего членов арифметической прогрессии равна 12, а ее четвертый член равен 12 . Найдите сумму первых пятнадцати членов прогрессии. A) 350 B) 300 C) 320 D) 360 Найдите числовое значение выражения: 2 B) 3,5 C) 2,5 D) 3 3tg 4 sin 2 3 cos2 6 Найдите наименьший положительный период функции y 2tg x 3 4 2 3 4 На каком из рисунков изображено решение системы неравенств x2 y2 36 x 1,5 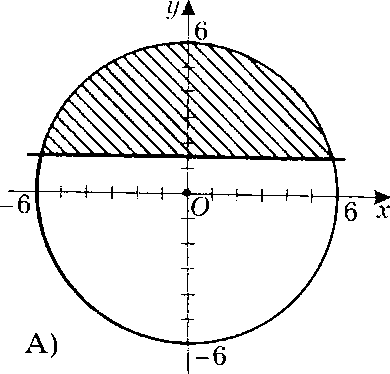 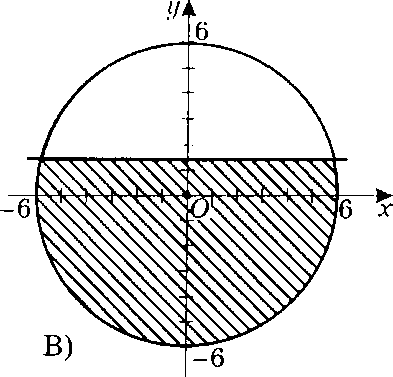 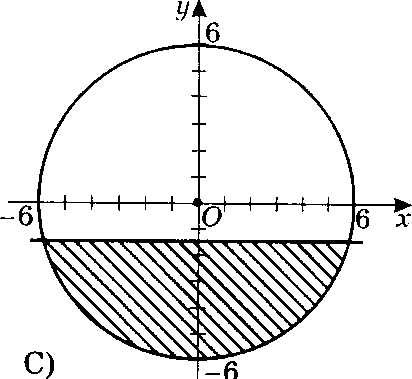 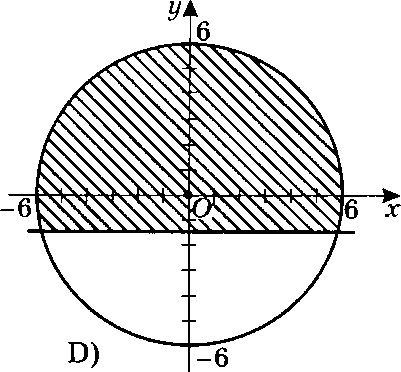 Вычислите tg, если cos 15 ; . 8 15 17 2 8 15 15 8 D) 15 8 Представьте бесконечную периодическую дробь 10,5(3) в виде обыкновенной дроби. A) 10 1 3 B) 10 8 15 C) 10 2 5 D) 10 7 15 costg Упростите выражение 0 tg - 1 tg sin 2 Задания уровня В Двое рабочих, совместно проработав 7 дней, выполнили всей работы. Они 4 закончили работу за 10 дней, хотя второй рабочий не вышел на работу последние 2 дня. За сколько дней закончит работу каждый рабочий в отдельности? Докажите тождество sin 720 sin180 cos720 cos180 1 Определите число членов геометрической прогрессии, если известно, что, если b4 b1 23, b6 b5 368, Sn 23
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
