|
|
Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся
Комплексная диагностическая работа по алгебре 10 класс 2021-2022 учебный год
автор:АрютинаСветланаИосифовна,педагог-эксперт,Северо-Казахстанскаяобласть,КГУ«Заградовскаясредняяшкола»КГУ«ОтделобразованияЕсильскогорайона»КГУ«Управлениеобразованияакимата Северо-Казахстанскойобласти»
Продолжительность – 45 минут
Количество баллов – 10 Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
|
№
задания
|
Тип
задания
|
Проверяемая цель
|
Нелинейные уравнения с двумя переменными и их
системы
|
А1
|
МВО
|
9.2.2.2 решать системы нелинейных уравнений с двумя переменными
|
Арифметическая прогрессия
|
А2
|
МВО
|
9.2.3.5 знать и применять формулы п-го члена, суммы п первых членов и характеристическое свойство
арифметической прогрессии
|
Геометрическая прогрессия
|
А3
|
МВО
|
9.2.3.6 знать и применять формулы п- го члена, суммы п первых членов и характеристическое свойство
геометрической прогрессии
|
Формулы тригонометрии
|
А4
|
МВО
|
9.2.4.4 выводить и применять формулы
приведения
|
Тригонометрические функции и их свойства
|
А5
|
МВО
|
9.2.4.6 объяснять с помощью единичной окружности чётность(нечётность),
периодичность, монотонность и
|
|
|
|
промежутки знакопостоянства
тригонометрических функций
|
Системы нелинейных
неравенств с двумя переменными
|
А6
|
МВО
|
9.2.2.4 решать системы нелинейных неравенств с двумя переменными
|
Тождественные преобразования
тригонометрических выражений
|
В1
|
РО
|
9.2.4.8 выполнять тождественные преобразования тригонометрических выражений
|
Нелинейные уравнения с двумя переменными и их
системы
|
В2
|
РО
|
9.4.2.1 решать текстовые задачи с помощью систем уравнений
|
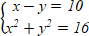 А1. А1. Система имеет:1 вариант Уровень А
одно решение; 2) четыре решения; 3) ни одного?
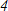 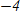 А2. А2. В арифметической прогрессии 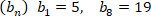 . Разность этой прогрессии равна: 1) ; 2) ; 3) 2. А3. В геометрической прогрессии 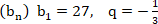 . Сумма первых её пяти членов равна: 3) 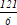 ; 2) 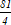 ; 3) 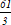 . А4. Чему равно значение 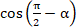  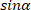 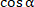  1) ; 2) ; 3) -sin ; 4) –cos А5. Выражение 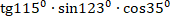 принимает значение:
равное нулю; 2) меньше нуля; 3) больше нуля.
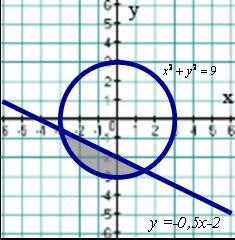
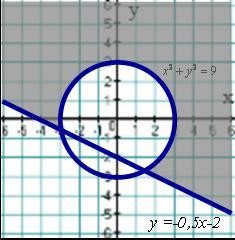
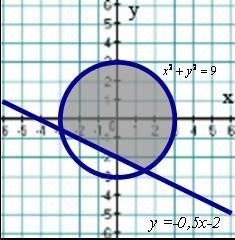
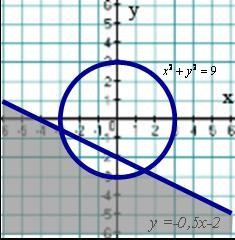
А6. На каком рисунке изображено множество решений системы неравенств х2 у2 9,
2 у х 4 0? Уровень ВВ1. Доказать тождество: 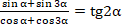 [2 балла] В2. Найдите два натуральных числа, если их среднее арифметическое равно 35, а их среднее геометрическое равно 28. [2 балла]
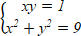 2 вариант Уровень А 2 вариант Уровень А
А1. Система имеет:
одно решение; 2) четыре решения; 3) ни одного?
А2. В арифметической прогрессии 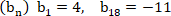 . Разность этой прогрессии равна: . Разность этой прогрессии равна:
2) 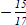 ; 2) ; 2) 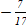 ; 3) 22,5. ; 3) 22,5.
А3. В геометрической прогрессии 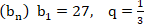 . Сумма первых её пяти членов равна: . Сумма первых её пяти членов равна:
1) 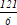 ; 2) ; 2) 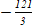 ; 3) ; 3) 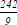 . .
А4. Чему равно значение 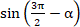
 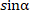 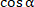  1) ; 2) ; 3) -sin ; 4) –cos 1) ; 2) ; 3) -sin ; 4) –cos
А5. Выражение 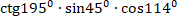 принимает значение: принимает значение:
меньше нуля; 2) больше нуля; 3) равное нулю.
А6. На каком рисунке изображено множество решений системы неравенств
х2 у2 9,
2 у х 4 0?
Уровень В
В1. Доказать тождество: 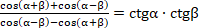 [2 балла] [2 балла]
В2. Найдите два натуральных числа, если их среднее арифметическое равно 61, а их среднее геометрическое равно 60. [2
балла]
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Определяет количество решений системы нелинейных уравнений с двумя переменными
|
А1
|
Умеет определять количество решений систем нелинейных
уравнений с двумя переменными
|
1
|
Вычисляют разность арифметической прогрессии,
используя формулу п-го члена
|
А2
|
Использует формулу вычисления разности
геометрической прогрессии
|
1
|
Определяют сумму первых п членов
|
А3
|
Использует формулу
|
1
|
геометрической прогрессии
|
|
нахождения суммы первых членов геометрической
прогрессии
|
|
Применяют формулу приведения
|
А4
|
Использует формулы
приведения
|
1
|
Используя промежутки
знакопостоянства определяют знак выражения
|
А5
|
Использует промежутки знакопостоянства
|
1
|
Находят решение систем нелинейных неравенств с двумя переменными
|
А6
|
Решает системы нелинейных
неравенств с двумя переменными
|
1
|
Используют тождественные преобразования тригонометрических выражений для доказательства тождеств
|
В1
|
Использует формулы тригонометрии для упрощения
выражения
|
1
|
Выполняет тождественные
преобразования
|
1
|
Решают текстовые задачи с помощью систем уравнений
|
В2
|
Вводит переменные и по
условию задачи составляет систему уравнений
|
1
|
Решает систему уравнений
|
1
|
Итого:
|
|
10
| |
|
|
 Скачать 1.19 Mb.
Скачать 1.19 Mb.