Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся

• Название: Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся
• Дата: 08.09.2022
• Размер: 1.19 Mb.
• Имя файла: 0.docx
• Тип: Методические рекомендации; #668278
• страница: 9 из 16

Комплексная диагностическая работа поалгебре9класс2021-2022учебныйгод

автор: Ткаченко Е.Ю. Костанайская область, г.Рудный, КГУ "Общеобразовательнаяшкола№1отделаобразованиягородаРудного"УправленияобразованияакиматаКостанайскойобласти, педагог-эксперт

Продолжительность – 45 минут

Типы заданий:

МВО – задания с множественным выбором ответов;

РО – задания, требующие развернутого ответа

Характеристика заданий

ТЕМА

№ задания

Тип задания

ПРОВЕРЯЕМАЯ ЦЕЛЬ

Квадратные корни и иррациональные выражения	1.1	МВО	8.1.2.1применять свойства арифметического квадратного корня;
Преобразования выражений, содержащих квадратные корни	1.2	МВО	8.1.2.4 освобождать от иррациональности знаменатель дроби
Решение квадратных уравнений	1.3	МВО	8.2.2.3 решать квадратные уравнения;
Решение квадратных уравнений	1.4	МВО	8.2.2.4 применять теорему Виета;
Квадратный трёхчлен	1.5	МВО	8.2.1.3 раскладывать квадратный трехчлен на множители;
Решение уравнений	1.6	МВО	8.2.2.5 решать уравнения вида |ax2+bx|+c=0; ax2+b|x|+c=0;
Решение уравнений	1.7	МВО	8.2.2.6 решать дробно-рациональные уравнения;
Квадратичная функция и её график	1.8	МВО	8.4.1.3 знать свойства и строить график квадратичной функции вида ;
Решение систем неравенств	2.1	РО	8.2.2.10 решать системы из двух неравенств, одно из которых линейное, а второе – квадратное;
Решение уравнений	2.2	РО	8.2.2.7 решать уравнения, приводимые к квадратным уравнениям;
Решение текстовых задач	2.3	РО	8.4.2.2 решать текстовые задачи с помощью дробно-рациональных уравнений;

1 вариант

Задания уровня А

Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.

1. 
   Какие свойства необходимо применить, чтобы преобразовать данное выражение:
   

1)

2)

3)

4)

5)

A) 1,2,3

^B) 1,2,4

^C) 1,2,5

D) 2,3,4

^E) 1,2,3,4,5

2. 
   Освободитесь от иррациональности в знаменателе дроби. А)
   

В)

С)

4. 
   х – 3 Е) х + 3
   

3. 
   Найдите корни уравнения: 5х² – 9х – 2 = 0 А) 2
   

В) -0,2

С) 2 и –0,2

D) – 2 и 0,2

4. 
   нет решения
   

4. 
   Если х₁ и х₂ - корни уравнения х² - 3х – 3 = 0, то найдите значение выражения
   

А) - 27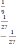

В) 27 С)

D)

E)

5. 
   Разложите квадратный трехчлен на множители: -х²+ 13х – 42 = 0 А) (х-6)(х-7)
   

В) (х+6)(х-7)

С) (х-6)(х+7)

D)(x+6)(x+7)

E)(6-x)(x-7)

6. 
   Найдите корни уравнения: x²+|x|-6=0 ^А)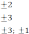
   

В)

С)

D)

^E)

7. 
   Найдите корни уравнения:
   

А) 1,5 и 2

В) 1,5

С) 2

4. 
   - 2
   
5. 
   0
   

8. 
   Определите координаты вершины параболы, используя формулы: 2х² +8х +9 = 0
   

А) (-2;1)

В) (2;33)

С) (-2;-1)

D) (2;-33)

Е) (2;-1)

Задания уровня В

1. 
   Решите систему неравенств: [4]
   
2. 
   Решите биквадратное уравнение: 9x⁴+5x²-4=0 [3]
   

2.3 Решите задачу с помощью дробно-рационального уравнения: [5]

Турист проплыл на лодке 3 км по течению реки и 2 км против течения реки за 30 минут. Найти скорость лодки в стоячей воде, если скорость течения реки 2км/ч.

2 вариант

Задания уровня А

Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.

1. 
   Какие свойства необходимо применить, чтобы преобразовать данное выражение:
   

1)

2)

3)

4)

5)

A) 1,2,3

^B) 1,2,4

^C) 1,2,5

D) 2,3,4

^E) 1,2,3,4,5

2. 
   Освободитесь от иррациональности в знаменателе дроби.
   

А)

В)

С)

D)

Е)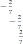

3. 
   Найдите корни уравнения: 7х² – 5х – 2 = 0 А) 1
   

В)

С) 1 и

4. 
   – 1 и
   
5. 
   нет решения
   

4. 
   Если х₁ и х₂ - корни уравнения х² - 2х – 2 = 0, то найдите значение выражения
   

А) - 4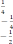

В) 4

С)

D)

E)

5. 
   Разложите квадратный трехчлен на множители: -х²+ 12х – 35 = 0 А) (х-5)(х-7)
   

В) (х+5)(х-7)

С) (х-5)(х+7)

D)(5-х)(x+7)

E)(x+5)(x-7)

6. 
   Найдите корни уравнения: x²-8|x|+12=0 ^А)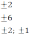
   

В)

С)

D)

^E)

7. 
   Найдите корни уравнения:
   

А) 8,5 и - 5

В) 8,5

С) 5

D) - 5

E) – 8,5

8. 
   Определите координаты вершины параболы, используя формулы: х²+4х – 21 = 0
   

А) (-2;25)

В) (2;9)

С) (-2;9)

D) (-2;-25)

Е) (2;-25)
Задания уровня В

1. 
   Решите систему неравенств: [4]
   
2. 
   Решите биквадратное уравнение: 4x⁴+3x²-1=0 [3]
   

2.3 Решите задачу с помощью дробно-рационального уравнения: [5]

Пароход прошёл 60 км по течению реки и затем обратно, затратив на весь путь 8 часов. Требуется определить собственную скорость парохода, если скорость реки течения реки 4 км/ ч.

Критерий оценивания	№ задания	Дескриптор	Балл
Применяет свойства	1.1	Выбирает свойства для	1

арифметического квадратного корня		преобразования выражения
Преобразовывает выражение, содержащее арифметический корень	1.2	Освобождается от иррациональности знаменатель дроби	1
Решает квадратные уравнения	1.3	Использует формулы корней квадратного уравнения и находит корни	1
Применяет теорему Виета	1.4	Использует теорему Виета для нахождения значения выражения	1
Раскладывает квадратный трехчлен на множители	1.5	Находит корни уравнения и раскладывает на множители	1
Решает уравнение вида | ax2+b|x|+c=0;	1.6	Находит корни уравнения	1
Решает дробно-рациональные уравнения	1.7	Использует алгоритм решения дробно рационального уравнения, находит корни	1
Знает свойства квадратичной функции вида ;	1.8	Использует формулы для нахождения вершины параболы	1
Решение систем неравенств	2.1	Решает линейное неравенство	1
		Решает квадратное неравенство	1
		Показывает решение обоих неравенств на числовых прямых	1
		Находит общее решение системы	1
Решает уравнения, приводимые к квадратным уравнениям;	2.2	Вводит замену переменной	1
		Решает квадратное уравнение	1
		Возвращается к замене и находит корни	1
решает текстовые задачи с помощью дробно-рациональных уравнений	2.3	вводит обозначение и связывает его с другими величинами	1
		составляет уравнение по условию задачи	1
		решает полученное уравнение	1
		исключает лишние корни;	1
		записывает ответ на вопрос задачи.	1
Итого			20