Комплекснаядиагностическаяработа
погеометрии10класс2021-2022учебный год
Авторы: Романович Юлия Ивановна, Костанайская область, Коммунальноегосударственноеучреждение"ГимназияотделаобразованияЖитикаринскогорайона"Управления образования акимата Костанайской области, педагог-исследовательБритвакЛюдмилаИвановнаСКО.Тайыншинскийрайон.КГУ''КраснополянскаяСШ''педагог-эксперт
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа
Характеристиказаданий
ТЕМА
|
№
задания
|
Тип
задания
|
ПРОВЕРЯЕМАЯ ЦЕЛЬ
|
Координаты вектора.
|
1.1
|
МВО
|
9.1.3.1 находить координаты вектора;
|
Угол между векторами.
Скалярное произаедение векторов
|
1.2
|
МВО
|
9.1.4.6 находить скалярное произведение векторов;
|
Сложение векторов
|
1.3
|
МВО
|
9.1.4.2 знать и применять правила сложения
векторов ;
|
Координаты вектора
|
1.4
|
МВО
|
9.1.3.2 находить длину вектора;
|
Осевая симметрия
|
1.5
|
МВО
|
9.1.4.9 строить образы фигур при симметриях,
параллельном переносе, повороте;
|
Признаки подобия
треугольников.
|
1.6
|
МВО
|
9.1.4.15 знать и применять подобие
прямоугольных треугольников
|
Углы, вписанные в
окружность
|
1.7
|
МВО
|
9.1.1.3 знать определение вписанного угла и его
свойства;
|
Площадь круга и его
частей
|
1.8
|
МВО
|
9.1.1.2 выводить и применять формулу
площади сектора, сегмента;
|
Теорема синусов и косинусов
|
2.1
|
РО
|
9.1.3.10 применять теоремы синусов и косинусов для решения треугольников и
прикладных задач;
|
Подобие фигур. Гомотетия.
|
2.2
|
РО
|
9.1.4.17 знать формулу зависимости между
площадями подобных фигур и коэффициентом подобия;
|
Правильные многоугольники и окружность
|
2.3
|
РО
|
9.1.2.5 знать и применять формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусы
вписанной и описанной окружностей правильного многоугольника;
|
I вариант
Задания уровня А
Вам предложены тестовые задания. Каждое здание оценивается в 1 балл.
Определите координаты вектора 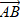 : если А(2;-1) и В(-4;2) A) : если А(2;-1) и В(-4;2) A) 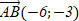
B) 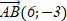
C) 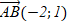
D) 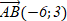
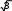 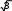 E) E) 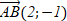
Найти скалярное произведение векторов: а (0;
5
3
6 D) 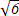
E) 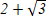 ) и в (2; ) и в (2; )
D) 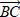
E) 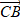
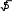 Найти длину вектора Найти длину вектора 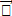 (7; ) (7; )
54
74 C) 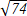 D) D) 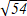
E) 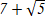
Сколько осей симметрии имеет правильный шестиугольник
5
3
6
4
2
В прямоугольном треугольники АВС ( С=900). Найдите высоту СН, если АН =3 см, ВН=6 см
A) 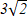
B) 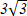
C) 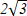
D) 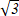
E) 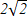
Найдите вписанный угол, опирающийся на дугу, которая составит 2/5 окружности. A) 540
B) 660
C) 600
D) 720
E) 1440
Найти площадь сектора круга радиусом 2, если соответствующий этому сектору центральный угол равен 600
23
3
6
34
15
Задания уровня В
В треугольнике АВС АС=12см, А=750, С=600. Найдите АВ и площадь треугольника
[6]
Найдите коэффициент подобия двух квадратов, если периметр первого равна 24см, а сторона второго квадрата 18см.
Квадрат со стороной 6
[2] 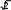 вписан в окружность. Найдите сторону правильного треугольника описанного около этой окружности. II вариантЗадания уровня АВам предложены тестовые задания. Каждое здание оценивается в 1 балл.1.1 Определите координаты вектора 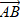 : если А(-1;3) и В(4;2) A) 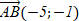 B) 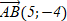 C) 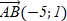 D) D) 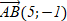 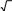 E) E) 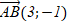
Найти скалярное произведение векторов:
5
|
а (5;
|
5 ) и в (2;0)
|
10
25
D) 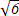
|
|
|
E) 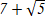
1.3
|
|
Упростите выражение:
| 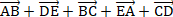 A) A) 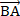 B) 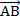 C) 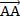 D) D)  E) E) 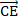
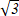 Найти длину вектора а (-6; ) Найти длину вектора а (-6; )
39
47 C) 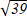 D) D) 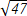
E) 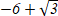
Сколько осей симметрии имеет ромб
0
3
[3]
1
4
2
В прямоугольном треугольники АВС ( С=900). Найдите высоту СН, если АН =3 см, ВН=9 см
A) 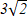
B) 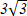
C) 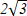
D) 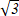
E) 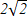
Найдите вписанный угол, опирающийся на дугу, которая составит 7/12 окружности. A) 1540
B) 1000
C) 1600
D) 2100
E) 1050
Найти площадь сектора круга радиусом 2, если соответствующий этому сектору центральный угол равен 600
3
6
2
15
Задания уровня В
В треугольнике АВС АС=10см, А=750, С=450. Найдите АВ и площадь треугольника
[6]
Найдите коэффициент подобия двух квадратов, если периметр первого равна 36см, а сторона второго квадрата 18см.
Квадрат со стороной 4
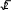 вписан в окружность. Найдите сторону правильного [2]
треугольника описанного около этой окружности.
[3]
Вариант 1
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Находит координаты вектора
|
1.1
|
D
|
1
|
Находит скалярное произведение векторов
|
1.2
|
B
|
1
|
Выполняет преобразование, применяет
правила сложения векторов
|
1.3
|
B
|
1
|
Находит длину вектора
|
1.4
|
D
|
1
|
Строит образы фигур при симметриях,
параллельном переносе, повороте
|
1.5
|
С
|
1
|
Применяет подобие прямоугольных
треугольников при решении задач
|
1.6
|
А
|
1
|
Находит вписанный угол, опирающийся на дугу, применяет определение вписанного
угла и его свойства
|
1.7
|
D
|
1
|
Применяет формулу площади сектора,
сегмента при решении задач
|
1.8
|
А
|
1
|
Применяет теоремы синусов и косинусов для решения треугольников и прикладных задач
|
2.1
|
использует свойство суммы углов
треугольника
|
1
|
находит угол В
|
1
|
использует теорему синусов
|
1
|
вычисляет сторону АВ
|
1
|
использует формулу площади
треугольника
|
1
|
вычисляет площадь треугольника
|
1
|
Знает и применяет формулу зависимости между площадями подобных фигур и коэффициентом подобия
|
2.2
|
применяет формулу зависимости между площадями подобных
фигур и коэффициентом подобия
|
1
|
вычисляет коэффициент подобия
|
1
|
Знает и применяет формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусы вписанной и описанной окружностей правильного многоугольника
|
2.3
|
использует формулу a4=
|
1
|
вычисляет радиус описанной
окружности
|
1
|
использует формулу 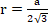 и вычисляет сторону треугольника и вычисляет сторону треугольника
|
1
|
Итого
|
19
|
Вариант 2
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Находит координаты вектора
|
1.1
|
D
|
1
|
Находит скалярное произведение векторов
|
1.2
|
B
|
1
|
Выполняет преобразование, применяет
правила сложения векторов
|
1.3
|
C
|
1
|
Находит длину вектора
|
1.4
|
C
|
1
|
Строит образы фигур при симметриях,
параллельном переносе, повороте
|
1.5
|
E
|
1
|
Применяет подобие прямоугольных
треугольников при решении задач
|
1.6
|
B
|
1
|
Находит вписанный угол, опирающийся на
дугу, применяет определение вписанного угла и его свойства
|
1.7
|
E
|
1
|
Применяет формулу площади сектора,
сегмента при решении задач
|
1.8
|
А
|
1
|
Применяет теоремы синусов и косинусов для решения треугольников и прикладных задач
|
2.1
|
использует свойство суммы углов
треугольника
|
1
|
находит угол В
|
1
|
использует теорему синусов
|
1
|
вычисляет сторону АВ
|
1
|
использует формулу площади
треугольника
|
1
|
вычисляет площадь треугольника
|
1
|
Знает и применяет формулу зависимости между площадями подобных фигур и коэффициентом подобия
|
2.2
|
применяет формулу зависимости
между площадями подобных фигур и коэффициентом подобия
|
1
|
вычисляет коэффициент подобия
|
1
|
Знает и применяет формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусы вписанной и описанной окружностей правильного многоугольника
|
2.3
|
использует формулу a4=
|
1
|
вычисляет радиус описанной
окружности
|
1
|
использует формулу 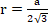 и вычисляет сторону треугольника и вычисляет сторону треугольника
|
1
|
Итого
|
19
| |
 Скачать 1.19 Mb.
Скачать 1.19 Mb.
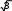 E)
E) 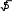 Найти длину вектора
Найти длину вектора 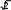 вписан в окружность. Найдите сторону правильного
вписан в окружность. Найдите сторону правильного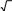 E)
E) 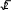 вписан в окружность. Найдите сторону правильного
вписан в окружность. Найдите сторону правильного