Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
Диагностическая контрольная работа по геометрии 10 класс 2021-2022 учебный год автор:АрютинаСветланаИосифовна,педагог-эксперт,Северо-Казахстанскаяобласть,КГУ«Заградовскаясредняяшкола»КГУ«ОтделобразованияЕсильскогорайона»КГУ«Управлениеобразованияакимата Северо-Казахстанскойобласти» Продолжительность – 45 минут Количество баллов – 10 Типы заданий: МВО – задания с множественным выбором ответов; РО – задания, требующие развернутого ответа. Характеристика заданий
1 вариант Уровень А А1. По координатам точек А (10; 5), В (– 9; 9) и С(-17; 11) определите каковы эти векторы коллинеарны; 2) равные; 3) сонаправленные; 4) равной длины. А3. Найдите длину вектора p(-4;5) 1) -36; 2) -6; 3) 6; 4) 36 А4. Если скалярное произведение векторов равно нулю, то угол между векторами: 1) тупой; 2) развернутый; 3) острый; 4) прямой. А5. Сколько осей симметрии имеет равносторонний треугольник? Одну 2) Две 3) Три 4) Не имеет осей симметрии А6. Периметр одного из 2х подобных треугольников равен 48 см, а коэффициент подобия этих треугольников равен 2. Чему может быть равен периметр второго треугольника? 1) 96 см; 2) 24 см; 3) 50 см; 4) 46 см. Уровень В В1. Две стороны треугольника равны 6 см и 16 см, а угол между ними - периметр и площадь треугольника. [2 балла] В2. Площадь круга, описанного около квадрата АВСД, равна 8π (пи) см2 (в квадрате). Найдите сторону и площадь треугольника ДАВ. [2 балла] 2 вариант Уровень А А1. По координатам точек А (12; 1), В (13; 0), С(1; 8) и Д(2;7) определите каковы эти векторы коллинеарны; 2) равные; 3) сонаправленные; 4) равной длины. А3. Найдите длину вектора p(3;-4) 1) 25; 2) 5; 3) -5; 4) -25 А4. Чему равен угол между противоположно направленными векторами: 1) нулю; 2) 90 градусов; 3) 180 градусов; 4) любому положительному числу А5. Сколько осей симметрии имеет разносторонний треугольник? Одну 2) Две 3) Три 4) Не имеет осей симметрии А6. Периметр одного из 2х подобных треугольников равен 26 см, а коэффициент подобия этих треугольников равен 2. Чему может быть равен периметр второго треугольника? 2) 52 см; 2) 13 см; 3) 28 см; 4) 24 см. Уровень В В1. Две стороны треугольника равны 6 см и 10 см, а угол между ними - балла] В2. Площадь круга, описанного около квадрата АВСД, равна 12π (пи) см2 (в квадрате). Найдите сторону и площадь треугольника ДАВ. [2 балла]
Комплекснаядиагностическаяработа поалгебреиначаламанализа11класс2021-2022учебныйгод  Авторы: Середкин В.П. учитель математики, педагог-мастер, Павлодарская область,Павлодарскийрайон, КГУ ЧернорецкаяСОШ №1., Авторы: Середкин В.П. учитель математики, педагог-мастер, Павлодарская область,Павлодарскийрайон, КГУ ЧернорецкаяСОШ №1.,Подгорнова О.В. учитель математики, педагог-исследователь, ВКО, Шемонаихинскийрайон,КГУ«Убинскаяобщеобразовательнаясредняяшкола»отделаобразованияпоШемонаихинскомурайонууправленияобразованияВКО Продолжительность – 45 минут Типы заданий: МВО – задания с множественным выбором ответов; РО – задания, требующие развернутого ответа Характеристиказаданий
1 вариант Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. Даны функции f(x) 2x 3 и g(x) x2 5 . Найдите g( f(x)) A) 4x2 12x14 B) 4x2 12x 5 C) 4x2 12x 4 + D) 4x2 12x 4 E) 4x2 12x 5 График, какой функции изображен на рисунке? 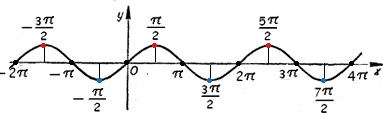 y sin 2x y sin x+ y sin 1 x 2 y 2sin x y 1 sin x 2 Вычислите: arctg 7 12 arcctg(1) arctg( 3 ) 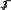 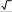 3 35 12 C) 5 12 D) 7 12 E) 9 12 Решите уравнение 2 cos x 8 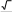 2 2A) 1n 4 n, n Z 4 n, n Z 4 n, n Z 2 4 4 2n, n Z 2n, n Z В корзине 6 яблок и 5 апельсинов. Наугад выбирают три фрукта. Какова вероятность, что все три фрукта – яблоки. 4 33 6 33 5 33 11 33 1 33 x2 5x 6 Вычислите lim x3 3x2 9x 4 27 1 27 5 27 11 27 6 27 Укажите уравнение касательной к графику функции, f(x) 2x2 1 проходящую через точку x0 1 y 4x y 4x 3 y 4x 3 y 4x E) y 4x 3 Найти математическое ожидание дискретной случайной величины X, заданной законом распределения
1 B) 7,22 C) 7,2 D) 72,2 E) 6,22 Задания уровня В Исследуйте функцию y x3 5 x2 2x 3 и постройте ее график [5] 2 2  Решите неравенство cos3x 1 2 Решите неравенство cos3x 1 22 [3] 2.3 Решите уравнение x3 x2 4x 2 0 [3] 2 вариант Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. Даны функции f(x) 3x 2 и g(x) x2 1. Найдите g( f(x)) A) 9x2 12x 3 B) 9x2 12x 5 C) 9x2 12x 6 D) 9x2 12x 3 E) 9x2 12x 5 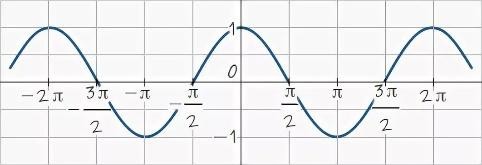 График, какой функции изображен на рисунке? График, какой функции изображен на рисунке?y cos2x y cos x y cos 1 x 2 y 2cos x y 1 cos x 2 Вычислите: arcctg A) 21 12 arcctg(1) arcctg( 3 )   3 35 12 12 4 E) 17 12 Решите уравнение 2sin x 12 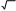 2 2A) 1n 3 B) 1n 6 C) 1n 3 D) 1n 6 E) 1n 4 n, n Z n, n Z 2n, n Z 2n, n Z n, n Z В ящике 6 яблок и 9 груш. Наудачу извлекают три фрукта. Какова вероятность того, что все три фрукта – яблоки. 4 91 6 91 5 91 11 91 1 91 x2 3x 2 Вычислите lim x 2 2x2 4x 3 4 1 4 5 4 1 2 7 4 Укажите уравнение касательной к графику функции f(x) 3x2 2 проходящую через точку x0 1 y 6x y 6x 5 y 6x 7 y 6x E) y 6x 5 Найти математическое ожидание дискретной случайной величины X, заданной законом распределения
1 B) 6,96 C) 9,6 D) 96,9 E) 9,69 3 Исследуйте функцию f(x)= х 3 х2 2 Задания уровня В 2х 3 и постройте ее график [5] 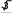 Решите неравенство sin 2x Решите неравенство sin 2x 4 2 [3] 2.3 Решите уравнение x3 x2 4x 6 0 [3]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
