|
|
Методические рекомендации для учителя математики Организация работы по восполнению пробелов в званиях учащихся
Комплекснаядиагностическаяработа погеометрии8класс2021-2022учебныйгод
Авторы:КуатбековаАлмагульСаламатовна,КарагандинскаяобластьБухар-ЖыраускийрайонКГУ«ОбщеобразовательнаяшколаимениТалгатаБигелдинова»отдела образования Бухар-Жырауского района управления образования Карагандинскойобласти,педагог-эксперт
СтуроваОльгаАнатольевна,ЖамбылскаяобластьТаласскийрайонг.КаратауКГУ
«ШКОЛА ЛИЦЕЙ №1 отдела образования Таласского района управления образованияакиматаЖамбылскойобласти»,категория высшая
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристиказаданий
ТЕМА
|
№
задания
|
Тип
задания
|
ПРОВЕРЯЕМАЯ ЦЕЛЬ
|
Аксиомы и теоремы
|
1.1
|
МВО
|
7.1.2.1 знать и применять аксиомы
расположения точек на прямой и на плоскости (аксиома порядка);
|
Свойства смежных и вертикальных углов
|
1.2
|
МВО
|
7.1.1.10 доказывать и применять свойства вертикальных и смежных
углов;
|
Медианы, биссектрисы, высоты треугольника
|
1.3
|
МВО
|
7.1.1.12 знать определение медианы, биссектрисы, высоты,
треугольника и изображать их;
|
Признаки равенства треугольников
|
1.4
|
МВО
|
7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на
доказательство;
|
Признаки параллельности прямых
|
1.5
|
МВО
|
7.1.2.5 применять признаки параллельности прямых при решении
задач;
|
Сумма углов треугольника.
|
1.6
|
МВО
|
7.1.1.17 применять теорему о сумме
|
|
|
|
внутренних углов треугольника и
следствия из неё при решении задач;
|
Неравенство треугольника
|
1.7
|
МВО
|
7.1.1.20 знать соотношение между
сторонами и углами треугольника и применять его при решении задач;
|
Окружности, описанная около треугольника и вписанная в треугольник
|
1.8
|
МВО
|
7.1.2.14 знать определения окружностей, вписанной в
треугольник и описанной около треугольника;
|
Свойства параллельности прямых
|
2.1
|
РО
|
7.1.2.7 применять свойства параллельных прямых при решении
задач
|
Свойства прямоугольного
треугольника
|
2.2
|
РО
|
7.1.1.27 применять свойства
прямоугольного треугольника
|
Внешний угол треугольника
|
2.3
|
РО
|
7.1.1.19 применять теорему о внешнем угле треугольника
|
1 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое задание оценивается в 1 балл.
Точка С лежит на отрезке АВ. Сравните длины отрезков А) АС > АВ
В) CB=AB С) АВ <СВ
АВ =АС
СВ < АВ
Чему равен угол между биссектрисами смежных углов? A) 600
B) 900
C) 1000
D) 450 E)1800
В треугольнике АВС АК - медиана, ВК= 4,6 см. Чему равна длина отрезка КС?
6,9 cм В) 2,3 см
9,2 см
4,6 см
4 см
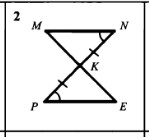 Выберите признак равенства треугольников на рисунке. Выберите признак равенства треугольников на рисунке.
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
по трем сторонам
по стороне и двум углам
по трем углам
Две прямые пересечены секущей. Чему равна сумма внутренних односторонних углов, если внутренние накрест лежащие углы равны?
A) 1800
B) 900
C) 00
D) 600
E) 300
1.6. Найдите 1, 2, 3.
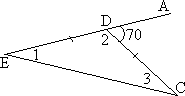
А) 60◦, 60◦, 60 B) 35◦, 110◦,35◦
C) 20◦, 80◦, 80◦
D) 30◦, 30◦, 120◦
E) 500; 650; 650
Найдите самый маленький угол в треугольнике АВС, если АВ < АС < ВС. А) С
В
А
все углы равны
невозможно определить
Окружность называется вписанной в треугольник, если она…
пересекает его стороны;
проходит через его вершины;
касается одной стороны;
проходит через одну из вершин;
касается всех его сторон.
Задания уровня В
  2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=48 , ∠2=57 . [4] 2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=48 , ∠2=57 . [4]
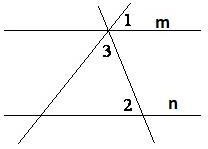
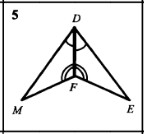
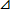  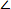 В AMD : , МС – биссектриса , DCM = 63°. В AMD : , МС – биссектриса , DCM = 63°.
 Найдите: DAM [3] Найдите: DAM [3]
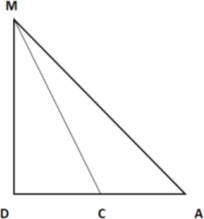
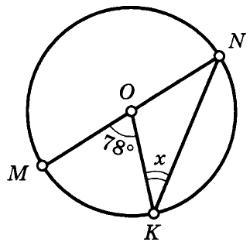 Найдите х [3] Найдите х [3]
2 вариант
Задания уровня А
Вам предложены тестовые задания. Каждое задание оценивается в 1 балл.
Точка В лежит на отрезке АС. Сравните длины отрезков:
А) АС > АВ
СВ < АC
АВ < СВ
АВ = АС
BC = AC
Найдите угол между биссектрисами вертикальных углов? A) 450
B) 900
C) 1800
D) 600
E) 1200
В треугольнике КМС КР- биссектриса, угол МКС = 780. Чему равна градусная мера угла МКР?
A) 900
B) 780
C) 360
D) 1560
E) 390
 По какому признаку равны треугольники на рисунке? По какому признаку равны треугольники на рисунке?
по двум сторонам и углу между ними
по стороне и двум прилежащим к ней углам
по трем сторонам
по стороне и двум углам
по трем углам
Сумма внутренних накрест лежащих углов при параллельных прямых и секущей равна 2200. Чему равны эти углы?
A) 1800
B) 900
C) 1100
D) 2200
E) 1000
1.6. Найдите 1, 2, 3.
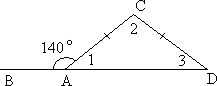
А) 40◦,100◦, 40◦ B) 420◦, 20◦, 140◦
C) 60◦,40◦, 80◦
D) 30◦,30◦, 120◦
E) 20◦, 80◦, 80◦
Найдите самый больший угол в треугольнике АВС, если АВ < АС < ВС. А) С
В
А
все углы равны
невозможно определить
Окружность называется описанной около треугольника, если она…
пересекает его стороны;
проходит через его вершины;
касается его сторон;
проходит через одну из вершин;
проходит через две вершины.
Задания уровня В
  2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=36 , ∠2=75 . [4] 2.1. Прямые m и n параллельны. Найдите ∠3, если ∠1=36 , ∠2=75 . [4]

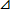 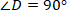 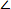 В AMD : , МС – биссектриса , DCM = 72°. В AMD : , МС – биссектриса , DCM = 72°.
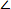 Найдите: DAM [3] Найдите: DAM [3]

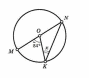 Найдите х [3] Найдите х [3]
84
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Сравнивает длины отрезков
|
1.1
|
Применяет аксиомы расположения точек на прямой и сравнивает длины
отрезков
|
1
|
Определяет угол между биссектрисами
|
1.2
|
Применяет свойства вертикальных и
смежных углов и находит угол между биссектрисами
|
1
|
Находит длину отрезка
(находит градусную меру угла)
|
1.3
|
Использует определения медианы и
биссектрисы треугольника и находит длину отрезка и величину угла
|
1
|
Выбирает признак равенства треугольников
|
1.4
|
Знает признаки равенства
треугольников и может по рисунку дать правильный ответ
|
1
|
Вычисляет сумму углов при
параллельных прямых и секущей
|
1.5
|
Применяет признаки параллельности
прямых при решении задач и вычисляет сумму углов
|
1
|
Находит углы треугольника
|
1.6
|
Применяя теорему о сумме внутренних углов треугольника и следствия из нее и свойства равнобедренного треугольника, находит углы
треугольника
|
1
|
Определяет меньший (больший) угол в
треугольнике
|
1.7
|
Знает соотношение между сторонами и углами треугольника и применяет его
при решении задачи
|
1
|
Знает определения окружностей, вписанной в треугольник и описанной
около треугольника;
|
1.8
|
Использует определения окружностей, вписанной в треугольник и описанной около треугольника и делает
правильный выбор
|
1
|
Находит неизвестный угол, используя свойства параллельных прямых
|
2.1
|
Находит градусную меру вертикального
угла
|
1
|
Находит градусную меру накрест
лежащего угла
|
1
|
Определяет развернутый угол и его
градусную меру
|
1
|
Находит неизвестный угол
|
1
|
Использует свойства прямоугольного треугольника для нахождения неизвестных
углов
|
2.2
|
Находит неизвестный угол MCD
|
1
|
Использует определение биссектрисы угла и находит М
|
1
|
Находит искомый угол треугольника
|
1
|
Использует теорему о внешнем угле треугольника
|
2.3
|
Определяет вид KON
|
1
|
Применяет теорему о внешнем угле
треугольника, находит сумму углов
|
1
|
Находит значение х
|
1
|
Итого
|
18
|
Комплексная диагностическая работа по алгебре 8 класс 2021-2022 учебный год
автор: Черненко Наталья Дмитриевна, педагог-исследователь, Северо-Казахстанскаяобласть, КГУ «Воскресеновская средняя школа» КГУ «Отдел образования Мамлютскогорайона»КГУ«Управлениеобразованияакимата Северо-Казахстанскойобласти»
Продолжительность – 45 минут
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Характеристика заданий
Тема
|
№
задания
|
Тип
задания
|
Проверяемая цель
|
Степень с целым
показателем
|
А1
|
МВО
|
7.1.2.15 применять свойства степени с
натуральным показателем
|
Формулы сокращённого умножения
|
А2
|
МВО
|
7.2.1.10 знать и применять формулы сокращённого умножения
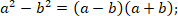
|
Многочлены.
|
А3
|
МВО
|
7.2.1.6 приводить многочлен к стандартному виду;
7.2.1.11 знать и применять формулы сокращённого умножения
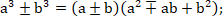
|
Линейная функция и её график
|
А4
|
МВО
|
7.4.1.5 знать определение линейной функции 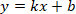
|
Одночлены и действия
над ними
|
А5
|
МВО
|
7.2.1.3 записывать одночлен в стандартном
виде;
|
Вариационные ряды
|
А6
|
МВО
|
7.3.3.1 усвоить понятия генеральной
совокупности, случайной выборки, вариационного ряда, варианты;
|
Преобразования выражений с помощью
формул сокращённого умножения
|
В1
|
РО
|
7.2.1.15 выполнять тождественные преобразования алгебраических выражений
с помощью формул сокращённого умножения;
|
Тождественные
преобразования
|
В2
|
РО
|
7.2.1.21 выполнять преобразования
алгебраических выражений;
|
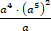 вариант вариант
А1. Упростите выражение:
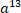 1) 2) a14 3) a 40 4) a39 5) a41 1) 2) a14 3) a 40 4) a39 5) a41
А2. Разложить на множители: 49-81d2
1) (7 – 81d)(7 + 81d) 2) (49 – 81d)(49 + 81d) 3) (7 -9d)(7 + 9d) 4)(49 – 9d)(49 + 9d) 5) 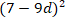
А3. Преобразуйте в многочлен стандартного вида: (4b2 + 6ab + 9b2)(2a – 3b) 2) (2a-3b)2 2) 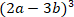 3) (2a+3b)2 4)(2a)3-(3b)3 5) 3) (2a+3b)2 4)(2a)3-(3b)3 5) 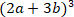
А4. Какие из точек А(0;4), В(1;8), С(2;-2,8), Д(10, -11,6), Е(-5;6,4) принадлежат графику линейной функции: y= -1,2х + 0,4
1) А 2) В 3) С 4) Д 5) Е
 А5. Упростите выражение: 100x6y3÷25x4y, и найдите его значение при x=3, y= - А5. Упростите выражение: 100x6y3÷25x4y, и найдите его значение при x=3, y= -
1) 4х²у², 9 2) 4х10у4 , 4380 3) х²у²,  4)75ху, - 4)75ху, - 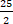 5) 4х²у², - 9 5) 4х²у², - 9
А6. Чему равна разность между наибольшим и наименьшим значением варианты ряда: 3º;7º; 1º; 4º; 0º; 5º; 1º; 3º; 6º; 4º; 9º; 2º
1) 8 2) 9 3) 7 4)1 5) 5
Уровень В В1. Решить уравнение: 5(х-4)² -(х+5)²=4х²+5
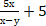 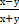 В2. Упростить выражение: ( )(1 - ) В2. Упростить выражение: ( )(1 - )
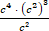 вариант вариант
А1. Упростите выражение:
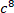 1) 2) c4 3) c 7 4) c12 5) c22 1) 2) c4 3) c 7 4) c12 5) c22
А2. Разложить на множители: 100a²-36b2
1)(100a –6b)(100a + 6b) 2) (10a –36b)(10a + 36b) 3) (10a -6b)(10a + 6b) 4)(100a – 36d)(100a + 36d)
5) 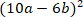
А3. Преобразуйте в многочлен стандартного вида: (4b2-6ab+9b2)(2a+3b)
2) (2a-3b)2 2) 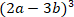 3) (2a+3b)2 4)(2a)3 + (3b)3 5) 3) (2a+3b)2 4)(2a)3 + (3b)3 5) 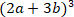
А4. Какие из точек А(0; 4), В(1; 8), С(2;-2,8), Д(10, -12,4), Е(-5;6,4) принадлежат графику линейной функции: y= -1,2х-0,4
1) А 2) В 3) С 4) Д 5) Е
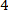 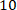 А5. Упростите выражение: 75x6y3÷15x4y, и найдите его значение при x=10, y= - А5. Упростите выражение: 75x6y3÷15x4y, и найдите его значение при x=10, y= - 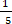 2) 5х²у², 20 2) 5х10у4 , 4380 3) х²у², 4) 5ху, - 5) 5х²у², - 20 2) 5х²у², 20 2) 5х10у4 , 4380 3) х²у², 4) 5ху, - 5) 5х²у², - 20
А6. Чему равна разность между наибольшим и наименьшим значением варианты ряда: 3º;7º; 1º; 4º;4 ; 5º; 1º; 3º; 6º; 4º; 9º; 2º;8º
3) 9 2) 8 3) 7 4)1 5) 5
Уровень В В1. Решить уравнение: 4(х+3)² -(х+2)²=3х² -8
В2. Упростить выражение: (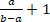 )( )( 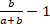 ) )
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Применяет свойства степени с натуральным показателем для упрощения выражения
|
А1
|
упрощает выражение, используя свойства степени с натуральным показателем: возведение степень в степень, умножение и
деление степеней с одинаковым основанием
|
1
|
Применяет формулу сокращенного умножения для разложения выражения
на множители
|
А2
|
представляет в виде произведения, используя формулу разности квадратов
|
1
|
Преобразует выражение в
многочлен стандартного вида
|
А3
|
Представляет выражение в виде
многочлена стандартного вида, используя формулу разности кубов
|
1
|
Определяет, какие из точек
принадлежат графику линейной функции
|
А4
|
Определяет, какие из точек принадлежат графику линейной функции
|
1
|
Выполняет деление одночленов, находит значение одночлена при
заданных значениях переменных
|
А5
|
Упрощает выражения, используя правило деления одночленов, свойства степени с натуральным показателем, и вычисляет
значение одночлена при заданных значениях переменных
|
1
|
Вычисляет разность между
наибольшим и наименьшим значением варианты ряда
|
А6
|
Находит наибольшую и наименьшую варианту, и вычисляет их разность.
|
1
|
Решает уравнение
|
В1
|
Применяет формулу квадрата суммы(разности) двух выражений, раскрывает скобки
|
1
|
Упрощает выражение и находит корень
уравнения
|
1
|
Выполняет упрощение алгебраических дробей
|
В2
|
Выполняет сложение и вычитание
алгебраических дробей
|
1
|
Выполняет умножение алгебраических
дробей
|
1
| |
|
|
 Скачать 1.19 Mb.
Скачать 1.19 Mb. Выберите признак равенства треугольников на рисунке.
Выберите признак равенства треугольников на рисунке.


 Найдите х [3]
Найдите х [3] По какому признаку равны треугольники на рисунке?
По какому признаку равны треугольники на рисунке?


 Найдите х [3]
Найдите х [3]