|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Тема:
|
Прикладные задачи на исследование квадратичных функций.
|
Цель обучения:
|
8.4.2.3 использовать квадратичную функцию для решения прикладных задач
|
Условие задачи:
|
Струя воды фонтана достигает наибольшей высоты 1,2 м на расстоянии 1 м от точки О выхода струи. Найти высоту струи на расстоянии 0,6 м от точки О.

|
Решение:
|
Введем систему координат. Пусть точка О – начало отсчета. Тогда вершина параболы имеет координаты (1; 1,2), а уравнение параболы имеет вид  . Поскольку точка О(0; 0) принадлежит параболе, то а = - 1,2. Найдем значение функции в точке х = 0,6: . Поскольку точка О(0; 0) принадлежит параболе, то а = - 1,2. Найдем значение функции в точке х = 0,6:
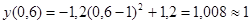
|
Ответ:
|
1 м.
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана для групповой работы, на этапе закрепления материала.
|
Тема:
|
Методы построения графиков функций. Использование цифровых ресурсов.
|
Цель обучения:
|
8.4.1.3 знать свойства и строить график квадратичной функции вида 
|
Условие задачи:
|
Построить график квадратичной функции заданной уравнением y=x^2+4*x-1
|
Решение:
|
1. Рисуем координатные оси, подписываем их и отмечаем единичный отрезок.
2. Значения коэффициентов а=1, b=4, c= -1. Так как а=1, что больше нуля ветви параболы направлены вверх.
3. Определяем координату Х вершины параболы Х вершины = -b/2*a = -4/2*1 = -2.
4. Определяем координату У вершины параболы
Увершины = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) – 1 = -5.
5. Отмечаем вершину и проводим ось симметрии.
6. Находим точки пересечения графика квадратичной функции с осью Ох. Решаем квадратное уравнение x^2+4*x-1=0.
х1=-2-√3 х2 = -2+√3. Отмечаем полученные значения на графике.
7. Находим точки пересечения графика с осью Оу.
х=0; у=-1
8. Выбираем произвольную точку B. Пусть она имеет координату х=1.
Тогда у=(1)^2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.
В результате получится такой график.

|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Задача используется для наработки навыков построения графиков по алгоритму. Можно использовать при объяснении материала. После построения графика в тетрадях, можно построить с помощью GeoGebra и оценить результаты.
|
Тема:
|
Методы построения графиков функций. Использование цифровых ресурсов.
|
Цель обучения:
|
8.4.1.3 знать свойства и строить график квадратичной функции вида 
|
Условие задачи:
|
Решите графически уравнение: х2 + 2х – 3 = 0
|
Решение:
|
Построим графики функций у=х2 и у=3-2х
Графиком функции у=х2 является парабола с вершиной в начале координат
График функции у=3-2х – прямая, построим её по таблице.
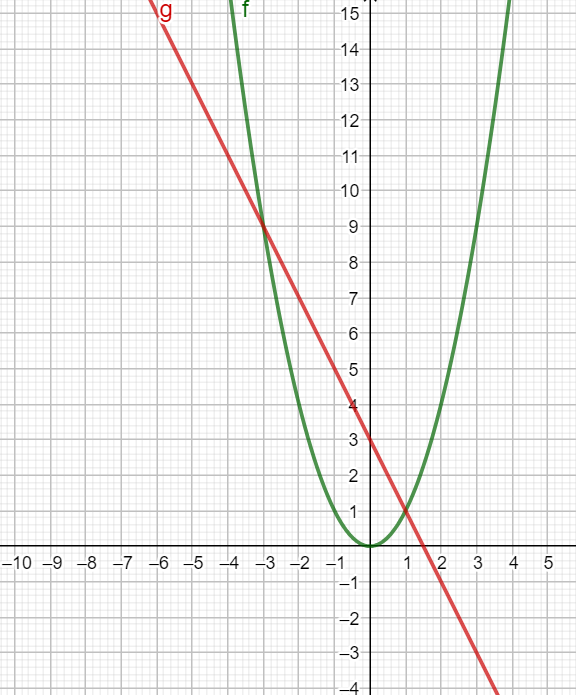
Построив графики обеих функций, найдем их точки пересечения: (-3;9), (1;1). Значит решением данного уравнения будут х=-3, х=1
Ответ:
|
Ответ:
|
х=-3, х=1
|
Методические рекомендации по использованию на уроке:
|
Задачу можно дать для решения в группах. После получения результата, можно построить график в GeoGebra и сравнить полученные результаты
|
Тема:
|
Методы построения графиков функций. Использование цифровых ресурсов
|
Цель обучения:
|
8.4.1.2 знать свойства и строить графики квадратичных функций вида y=a(x-m)2 , y=ax2 +n, y=a(x-m)2 +n, a≠0
|
Условие задачи:
|
Для каждого вида квадратичной функции найдите соответствующий график

     
2
3
4
6
5
1
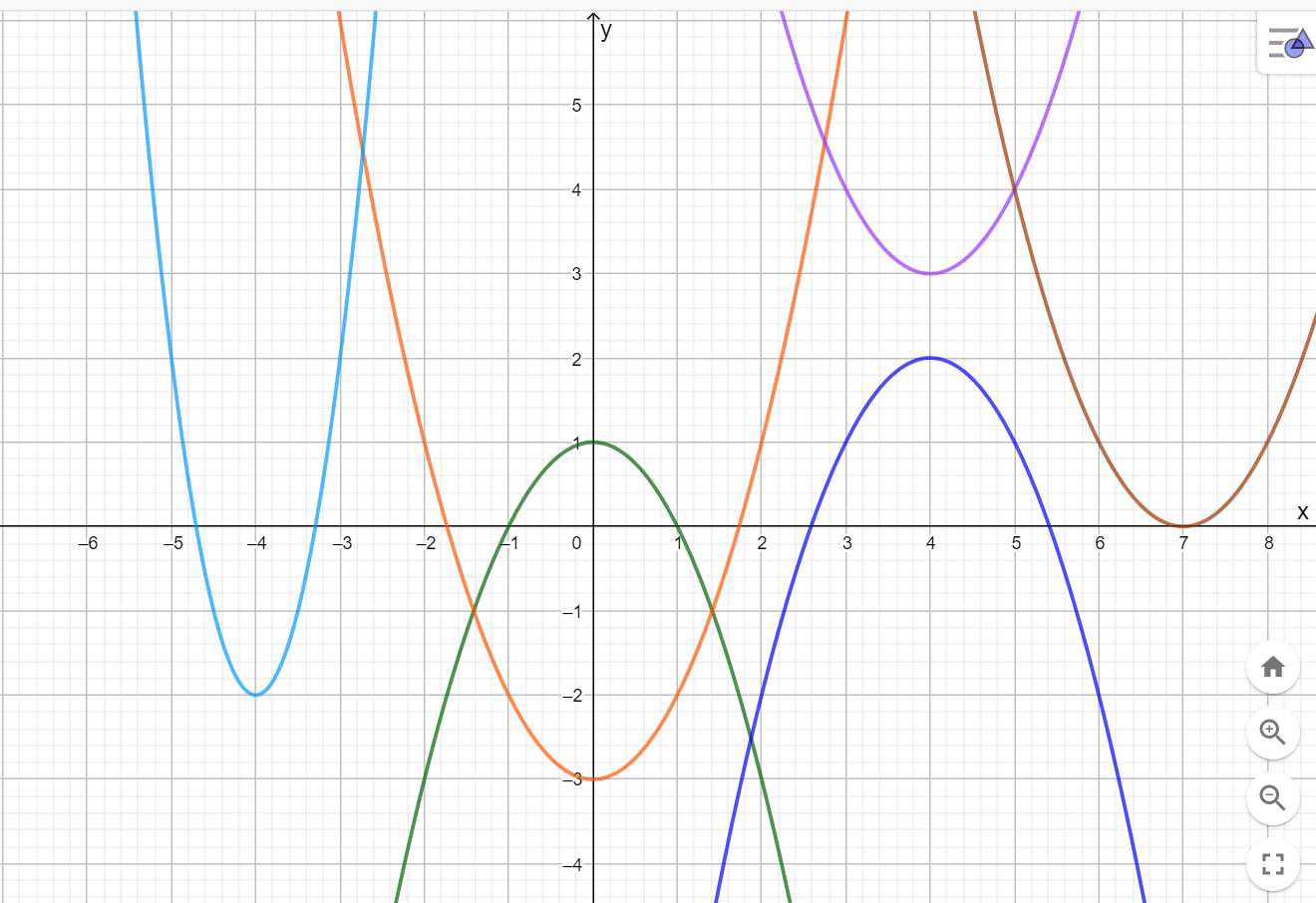
|
Ответ :
|
  5 5
 2 2
 3 3
 1 1
 6 6
 4 4
|
Методические рекомендации по использованию на уроке:
|
Задание можно применять как тренажер на уроках закрепления материала. Или же на этапе актуализации знаний. Рекомендовано для всех учащихся.
|
Тема:
|
Текстовые задачи на прогрессии.
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
При делении девятого члена арифметичекой прогрессии на ее второй член получается 5, а при делении 13-го члена этой прогрессии на ее шестой член, получается 2 и в остатке 5. Найти первый член прогрессии и ее знаменатель.
|
Решение:
|
По условию задачи составим систему:
 а9==5а2 а9==5а2
а13=2а6+5
 тогда, выразим все члены прогрессии через а1 и d тогда, выразим все члены прогрессии через а1 и d
a1+8d=5(a1+d)
a1+12d=2(a1=5d)+5
раскроем скобки и приведем подобные:
  4a1-3d =0 4a1-3d =0 4a1-3d =0 4a1-3d =0
a1-2d=-5 a1 =2d-5
решив систему способом подстановки найдем решения:
a1=3, d=4
|
Ответ:
|
a1=3, d=4
|
Методические рекомендации по использованию на уроке:
|
Данное задание можно дать для работы в группе, на этапе закрепления материала. Рассчитана на ученика уровня В. Для актуализации знаний повторить способы решения систем уравнений.
|
Тема:
|
Текстовые задачи на прогрессии
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями;
|
Условие задачи:
|
Человек заболевший гриппом может заразить 4 человек. Через сколько дней заболеет все население поселка в котором проживает 341 человек?
|
Решение:
|
1 день - 1 чел болен
2 день - 1 + 1*4 = 1 ( 1 + 4) = 5 чел болеют
3 день - 5 + 5*4 = 5 ( 1 + 4) = 25 чел болеют
4 день - 25 + 25*4 = 25 ( 1 + 4) = 125 чел болеют
5 день - 125 + 125*4 = 125 ( 1 + 4) = 625 чел болеют ≥ 341 ,
т.е всё население заболеет на 5-ый день
Т.о. мы получили числовую последовательность, первый член которой равен 1 , а каждый член начиная со второго можно выразить формулой:
Т.е. эта последовательность является геометрической прогрессией со знаменателем q=5.
|
Ответ:
|
через 5 дней.
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана для групповой работы;
Можно использовать в СОРе;
|
Тема:
|
Текстовые задачи на прогрессии.
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
В арифметической прогрессии  = 5, а сумма первых восьми членов равна 120. Найдите первый член и разность прогрессии. = 5, а сумма первых восьми членов равна 120. Найдите первый член и разность прогрессии.
|
Решение:
|
 = 5 = 5
S8 = 120
а1, d - ?
an = a1+ d(n-1)
Sn = 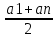 n S8 = n S8 =  *8 *8
a2 = a1 + d, a7 = а1+ 6d
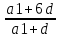 = 5 (1) = 5 (1)
120 =  *8 (2) *8 (2)
Решим (2) уравнение
120 = 4(a1 + а8)
30 = 2 а1 + 7d
Выразим а1
а1 = 15 - 3,5 d
подставим это выражение в первое уравнение
 = 5 = 5
15 + 2,5 d = 5 (15 - 2,5 d )
2,5 d + 12,5 d = 60
15d = 60
d = 4
a1 = 15 – 3.5 * 4 = 15 – 14 = 1
|
Ответ:
|
d = 4
a1 = 1
|
Методические рекомендации по использованию на уроке:
|
Задача очень подходит для групповой работы на уроке-обощения арифметической прогрессии в целом.
|
Тема:
|
Решение прикладных задач на оптимизацию. Графический способ решения систем неравенств.
|
Цель обучения:
|
9.2.2.4 решать системы нелинейных неравенств с двумя переменными
|
Условие задачи:
|
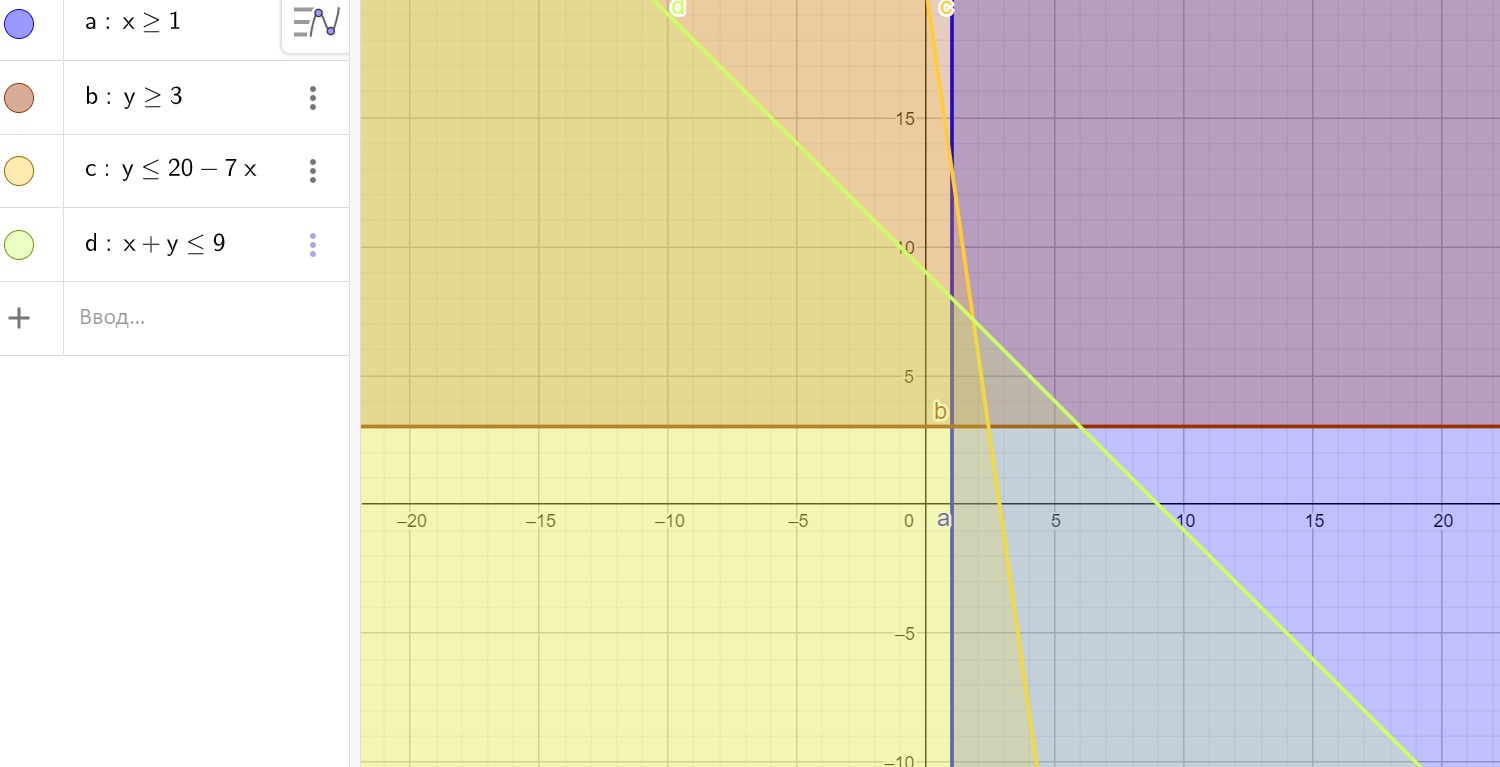
Кайрат купил х ручек и у карандашей. Цена 1 ручки- 35тг, карандаша 5 тг. Причем денег у Кайрата 100тг.
а) Выразите эту информацию в виде неравенства, содержащего x и y.
Известно, что количество купленных товаров удовлетворяет следующим неравенствам: 𝑥 ≥ 2, 𝑦 ≥ 5.
б) Кроме того, известно, что общее количество купленных товаров не превышает 15. Выразите эту информацию в виде неравенства, содержащего x и y.
с) На координатной плоскости изобразите область, удовлетворяющую системе четырех неравенств.
|
Решение:
|
а) 35х+5у≤100,
𝑥 ≥ 1, 𝑦 ≥ 3.
б) х+у≤9
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Задание можно использовать на этапе объяснения материала. Так же можно использовать для работы в группах или при первичном закреплении материала. Рассчитана на всех учащихся.
|
Тема:
|
Решение прикладных задач на оптимизацию. Графический способ решения систем неравенств.
|
Цель обучения:
|
9.2.2.4 решать системы нелинейных неравенств с двумя переменными
|
Условие задачи:
|
Стоимость (за один час перевозки) содержания баржи состоит из двух частей: стоимости топлива, пропорциональной кубу скорости баржи, и стоимости амортизации баржи ( зарплата команды, стоимость оборудования и т. д.). Общая стоимость содержания баржи за час выражается формулой:
S = av³ + b, где v- скорость судна в км/ч, a и b – коэффициенты, заданные для каждого судна (для нашего а=0,005, b=40).
Ясно, что расходы на топливо будут тем больше, чем быстрее движется корабль, остальные расходы от скорости не зависят.
Казалось бы, чем медленнее движется корабль, тем дешевле его эксплуатация. Так ли это?
|
Решение:
|
Решим данную задачу с помощью производной:
S/v = 0,005v² + 40/v,
Y′ = 0,005·2v – 40/v²,
Y′ = 0 ;
0,01v – 40/v² = 0
0,01v = 40/v²,
0,01v³ = 40,
v³ = 4000,
v ≈ 16 км/ч

|
Ответ:
|
Оптимальная скорость катера для минимальных затрат равна 16 км/ч
|
Методические рекомендации по использованию на уроке:
|
Лучше всего задачу решать на уроке решения задач в парах, осуществляя взаимопроверку по завершении решения большинством пар.
| |
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.