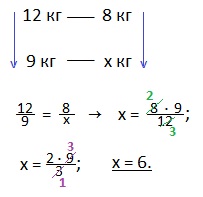|
стр
|
Методы решения текстовых задач
|
5
|
Решение текстовых задач с помощью пропорции. Задачи на нахождение масштаба, длины окружности, площади круга
|
5
|
Решение текстовых задач с помощью уравнений и неравенств.
|
8
|
Методы решения задач по статистике и теории вероятностей в основной школе
|
12
|
Элементы комбинаторики. Решение задач с использованием формул комбинаторики. Бином Ньютона и его свойства
|
12
|
Методы решения задач на событие и вероятность. Применение геометрической вероятности при решении задач
|
14
|
Элементы математической статистики. Вариационные ряды. Анализ информации по статистической таблице, полигону и гистограмме частот
|
16
|
Прикладные задачи на математическое моделирование и анализ
|
20
|
Прикладные задачи на исследование квадратичных функций.
|
20
|
Методы построения графиков функций. Использование цифровых ресурсов.
|
22
|
Текстовые задачи на прогрессии
|
26
|
Решение прикладных задач на оптимизацию. Графический способ решения систем неравенств
|
28
|
Решение задач планиметрии
|
31
|
Решение треугольников. Практические задачи геометрии
|
31
|
Векторы на плоскости. Применение векторов в решении геометрических задач
|
33
|
Преобразования плоскости. Методы решения задач с применением преобразований плоскости
|
36
|
Решение задач стереометрии
|
39
|
Способы решения задач на нахождение площади боковой и полной поверхности пространственных фигур. Использование графических редакторов при решении задач на сечение многогранника плоскостью
|
39
|
Методы решения задач на нахождение элементов тел вращения и объемов пространственных фигур
|
42
|
Комплексные числа. Основная теорема алгебры
|
48
|
Комплексные числа. Арифметические действия над комплексными числами
|
48
|
Комплексная плоскость. Модуль комплексного числа
|
50
|
Решение квадратных уравнений на множестве комплексных чисел. Основная теорема алгебры
|
51
|
Методы решения уравнений и неравенств в старшей школе
|
56
|
Решение уравнений высших степеней различными методами. Применение обобщенной теоремы Виета к многочленам третьего порядка
|
56
|
Методы решения иррациональных уравнений и неравенств
|
57
|
Методы решения тригонометрических уравнений и неравенств
|
60
|
Решение систем логарифмических, показательных уравнений и неравенств
|
60
|
Статистика и теория вероятностей в старших классах
|
63
|
Вероятность события и ее свойства. Правила сложения и умножения вероятностей
|
63
|
Задачи на нахождение вероятностей с применением формулы комбинаторики. Применение бинома Ньютона для приближённых вычислений
|
65
|
Формула полной вероятности. Применение формулы Байеса при решении задач. Формула Бернулли и ее следствия
|
67
|
Прикладные задачи на математическое моделирование и анализ в старших классах
|
71
|
Прикладные задачи на применение физического и геометрического смысла производной
|
71
|
Прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
72
|
Применение определенного интеграла для решения физических задач на вычисление работы и расстояния
|
74
|
Решение прикладных задач с использованием дифференциальных уравнений
|
77
|
Использованная литература
|
78
|
|
|
Тема:
|
Решение текстовых задач с помощью пропорции.
|
Цель обучения:
|
6.5.1.2 решать задачи на проценты с помощью пропорции;
|
Условие задачи:
|
В Коргалжынском государственном заповеднике обитает 363 вида птиц. Из них 42 вида занесены в Красную книгу Казахстана и 27 видов птиц в МСОП (Международный союз охраны природы). Определите сколько процентов составляют виды птиц, внесённых в Красную книгу Казахстана и сколько в МОСП? (Ответы запишите в десятичных дробях и округлите до десятых).
|
Решение:
|
Пусть х % - процент птиц в Красной книге
363 вида - 100%
42 вида – х %
х= = =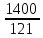 =11,6% =11,6%
Пусть х % - процент птиц в МОСП
363 вида - 100%
27 видов – х %
х=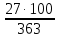 = = =7,4% =7,4%
|
Ответ:
|
в Красную книгу- 11,6%, в МОСП -7,4%
|
Методические рекомендации по использованию на уроке:
|
Содержание задачи основано на местном материале и можно использовать на интегрированных уроках математики и географии. Решать можно на первых уроках по теме «Пропорция», для наработки навыков применения пропорции. Для решения нужно повторить темы: «Округление чисел» и «Десятичные дроби».
Или же взяв один вопрос задачи можно включить в СОР (2 балла):
Дескриптор:
Составляет пропорцию -1 балл
Округляет десятичную дробь до разряда десятых -1 балл
|
Тема:
|
Решение текстовых задач с помощью пропорции.
Решение задач на отношения.
|
Цель обучения:
|
6.1.2.6 делить величины в заданном отношении;
|
Условие задачи:
|
Выберите из заданных чисел 9, 15, 18, 32, 49, 61 числа, которые можно разделить нацело в заданных отношениях.
И запишите результаты деления.
|
Решение:
|
Подсчитаем вначале сумму частей первого столбца 1+4=5 (частей)
Теперь нужно выбрать из заданных чисел, число кратное 5: 15
Чтобы найти числа, выполним деление 15:5=3. Получается в одной части – 3. Следовательно 1*3=3, 4*3=12
Значит, если число 15 разделить в отношении 1:4 получим 3 и 12
Аналогично с другими отношениями.
|
Ответ:
|
1:4
|
1:3
|
2:5
|
15
|
32
|
49
|
3 и 12
|
8 и 24
|
14 и 35
|
|
Методические рекомендации по использованию на уроке:
|
Данную задачу можно давать для закрепления алгоритма решения задач на деление величины в заданном отношении. Можно применять как тренажер для закрепления материала, так же при устном счете.
|
Тема:
|
Решение текстовых задач с помощью пропорции.
|
Цель обучения:
|
6.1.1.2 понимать, какие величины являются прямопропорциональными, приводить примеры, решать задачи;
|
Условие задачи:
|
Для малинового варенья взяли 12 кг малины и 8 кг сахара. Сколько сахара потребуется, если взяли 9 кг малины?
|
Решение:
|
Рассуждаем так:
Пусть потребуется х кг сахара на 9 кг малины. Масса малины и масса сахара — прямо пропорциональные величины: во сколько раз меньше малины, во столько же раз нужно меньше сахара. Следовательно, отношение взятой (по массе) малины (12:9) будет равно отношению взятого сахара (8:х). Получаем пропорцию:
12:9=8:х;
х=9·8:12;
х=6. Ответ: на 9 кг малины нужно взять 6 кг сахара.
Решение задачи можно было оформить и так:
Пусть на 9 кг малины нужно взять х кг сахара.
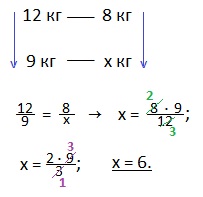
(Стрелки на рисунке направлены в одну сторону, а вверх или вниз — не имеет значения. Смысл: во сколько раз число 12 больше числа 9, во столько же раз число 8 больше числа х, т. е. здесь прямая зависимость).
|
Ответ:
|
на 9 кг малины надо взять 6 кг сахара.
|
Методические рекомендации по использованию на уроке:
|
Задача для групповой работы;
Для большинства учащихся;
|
Тема:
|
Решение текстовых задач с помощью линейных уравнений
|
Цель обучения:
|
8.4.2.1решать текстовые задачи с помощью квадратных уравнений;
|
Условие задачи:
|
Одну сторону смотровой площадки полигона (квадратной формы) увеличили на 2 м, а другую – на 1 м и получили участок прямоугольной формы площадью 12 м2. Найдите длину стороны первоначальной площадки.
|
Решение:
|
Пусть х м – первоначальная сторона, тогда (х + 2)м и (х + 1) м – стороны полученной площадки.
Зная, что площадь полученной
площадки равна 12 м2, составим
уравнение:
(х + 2) (х + 1) = 12;
х2 + х + 2х + 2 – 12 = 0;
х2 + 3х – 10 = 0;
D = 32 – 4 • 1 • (–10) = 9 + 40 = 49;
D > 0; 2 корня.
x1 = 2; x2 = –5.
Так как длина стороны выражается
положительным числом, то х2 = –5 – не удовлетворяет условию задачи.
|
Ответ:
|
2 см
|
Методические рекомендации по использованию на уроке:
|
Задача для большинства;
Использовать для закрепления данной темы;
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.
 =
=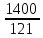 =11,6%
=11,6%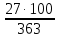 =
= =7,4%
=7,4%