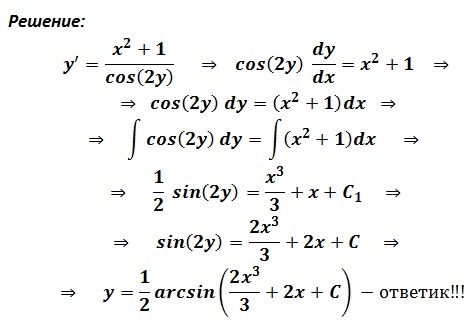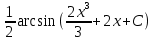|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Тема:
|
Применение определённого интеграла для решения физических задач на вычисление работы и расстояния
|
Цель обучения:
|
11.4.2.1 - применять определённый интеграл для решения физических задач на вычисление работы и расстояния
|
Условие задачи:
|
Скорость прямолинейного движения тела выражается формулой υ=2t+3t2 (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
|
Решение:
|
Физический смысл производной: если тело движется по закону S = S(t), то скорость тела в момент времени t0 равна значению производной функции S(t) в этой точке, т. е.
υ = Sꞌ(t0).
Тогда обратное утверждение: если скорость движения тела задана уравнением υ = υ (t), то путь, пройденный телом от момента времени t = a до момента времени t = b равен 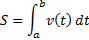 . Подставим уравнение скорости в формулу и рассчитаем путь. . Подставим уравнение скорости в формулу и рассчитаем путь.
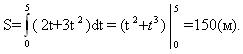
|
Ответ:
|
150м
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать как пример решения подобных задач на первом уроке. Или же при проблемном обучении можно дать в группах для самостоятельного поиска путей решения.
|
Тема:
|
Применение определённого интеграла для решения задач
|
Цель обучения:
|
11.4.1.9 - знать и применять формулу вычисления объема тела вращения с помощью определенного интеграла
|
Условие задачи:
|
Вычислить площадь фигуры, ограниченной линиями 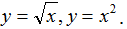
Решение: Построим на координатной плоскости графики функций 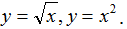 . Выделим площадь фигуры, которую надо найти. . Выделим площадь фигуры, которую надо найти.
|
Решение:
|
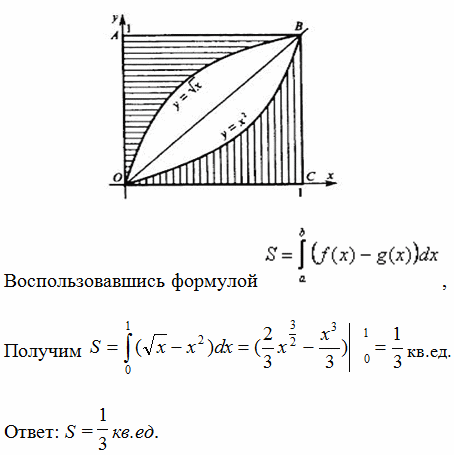
|
Ответ:
|
S=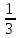 кв.ед кв.ед
|
Методические рекомендации по использованию на уроке:
|
Задача для закрепления данной темы;
Рассчитана для большинства;
|
Тема:
|
Применение определенного интеграла для решения физических задач
|
Цель обучения:
|
11.4.2.1 - применять определённый интеграл для решения физических задач
|
Условие задачи:
|
Сила упругости F пружины, растянутой на l1 = 0,05 м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 12 =0,1 м?
|
Решение:
|
Подставив данные в формулу закона Гука, получим: 3=k*0.05, т.е. k=60, следовательно, сила упругости выражается соотношением F=60x. Найдем работу переменной силы по формуле (2), полагая, что а=0; b=0,1:
A=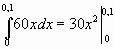 = 0,3Дж = 0,3Дж
|
Ответ:
|
0,3Дж
|
Методические рекомендации по использованию на уроке:
|
Чтобы решить данную задачу необходимо сначала повторить формулу силы упругости или закон Гука. Вычислить коэффициент упругости k пружины. И применить определенный интеграл для вычисления работы.
|
Тема:
|
Решение прикладных задач с использованием дифференциальных уравнений.
|
Цель обучения:
|
11.4.1.22 - знать основные понятия о дифференциальных уравнениях;
|
Условие задачи:
|
Известно 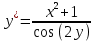 . Найдите у. . Найдите у.
|
Решение:
|
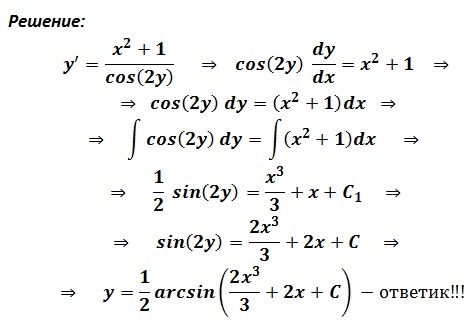
|
Ответ:
|
y=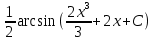
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана на среднего ученика. Можно использовать для работы в группе.
|
Список литературы
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2010
«Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования.
Курбанов К.О. Некоторые прикладные задачи по высшей математике (методическое пособие). – Махачкала: Махачкалинский филиал МАДГТУ, 2011 г. – 24стр.
Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
Геометрия 11 класс, А.В. Погорелов. – М.: Просвещение, 2002.
В.А. Кирзимов, Е.М. Белоногова "Преобразование плоскости", Москва -2000;
А.Е.Абылкасымова, Т.П.Кучер, В.Е.Корчевский, З.А. Жумагулова – Алгебра 9 класс
https://shkolkovo.net/catalog/slozhnye_zadachi_prikladnogo_haraktera/naibolshego_naimenshego_znacheniya_velichiny
https://shkolkovo.net/catalog/geometriya_v_prostranstve_stereometriya/ploshhad_i_obem_figur
Сборник задач по теории вероятностей (с решениями) | Материал для подготовки к ЕГЭ (ГИА) по алгебре (9, 11 класс): | Образовательная социальная сеть (nsportal.ru)
GeoGebra classic
И.П. Рустюмова, С.Т. Рустюмова. Тренажер по подготовке к ЕНТ по математике. 2009г. Алматы
|
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.
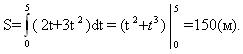

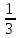 кв.ед
кв.ед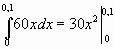 = 0,3Дж
= 0,3Дж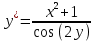 . Найдите у.
. Найдите у.