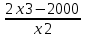Тема:
|
Формула полной вероятности. Применение формулы Байеса при решении задач. Формула Бернулли и ее следствия
|
Цель обучения:
|
10.3.2.8 - использовать формулу Бернулли и ее следствия при решении задач
|
Условие задачи:
|
Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.
|
Решение:
|
Искомая вероятность равна сумме вероятностей трех событий, состоящих в том, что герб не выпадет ни разу, либо один раз, либо два раза:
Р(А) = Р6(0) + Р6(1) + Р6(2) = 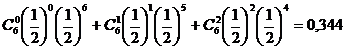
|
Ответ:
|
0,344
|
Методические рекомендации по использованию на уроке:
|
Задачу можно решать на уроке сразу после объяснения материала, для закрепления и наработки навыков применения формулы Бернулли. Рассчитана на всех учащихся.
|
Тема:
|
Формула полной вероятности. Применение формулы Байеса при решении задач. Формула Бернулли и ее следствия.
|
Цель обучения:
|
10.3.2.6 - знать формулу Байеса и применять ее при решении задач;
|
Условие задачи:
|
Группа из 12 стрелков включает в себя трёх мастеров спорта, четырёх кандидатов в мастера и пятерых перворазрядников. Мастер спорта может попасть в мишень с вероятностью 0,9, кандидат в мастера - с вероятностью 0,85, перворазрядник - с вероятностью 0,75. Наудачу выбранный стрелок сделал выстрел, мишень была поражена (событие А). Какова вероятность того, что этот стрелок является мастером спорта?
|
Решение:
|
Неизвестно, какой стрелок сделал выстрел. Имеются гипотезы: H1 - стрелял мастер спорта, H2 - стрелял кандидат в мастера, Нз - стрелял перворазрядник.
По условию, Р(H1)= 3/12, Р(H2)= 4/12, Р(Нз) = 5/12.
Кроме того, даны вероятности попадания для стрелков каждой группы: Р(А⁄ H1)= 0,9, Р(А ⁄ H2 )= 0,85, Р(А ⁄Нз) = 0,75. Вероятность того, что мишень была поражена наудачу выбранным стрелком - Р(А), по формуле полной вероятности будет: Р(А) = Р(H1) Р(А ⁄ H1) + Р(H2) Р(А ⁄ H2 )+ Р(Н3) Р(А ⁄ Н3) = (3∙0,9 + 4∙0,85 + 5∙0,75)/12≈ 0,821.
Тогда, вероятность того, что мишень была поражена мастером спорта, получится по формуле Байеса: Р(H1 ⁄А ) = Р(𝐻1)Р(𝐴⁄𝐻1) Р(А) = 3∙0,9 12∙0,821 ≈ 0,274
|
Ответ:
|
≈ 0,274
|
Методические рекомендации по использованию на уроке:
|
Задача для групповой работы;
|
Тема:
|
Формула полной вероятности. Применение формулы Байеса при решении задач. Формула Бернулли и ее следствия.
|
Цель обучения:
|
10.3.2.6. знать формулу Байеса и применять ее при решении задач
|
Условие задачи:
|
Имеются три урны; в первой 3 белых шара и 1 чёрный, во второй - 2 белых шара и 3 чёрных, в третьей - три белых шара. Некто подходит наугад к одной из урн и вынимает из неё один шар. Этот шар оказался белым. Найти послеопытные (апостериорные) вероятности того, что этот шар вынут из первой, второй, третьей урны. (из интернет ресурса)
|
Решение:
|
Гипотезы:
- выбрана первая урна;
- выбрана вторая урна;
- выбрана третья урна.
Так как урна выбирается наугад, то априорные вероятности гипотез раны:
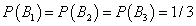 . .
В результате опыта появилось событие A - из выбранной урны вынут белый шар.
Условные вероятности события A относительно каждой из гипотез:
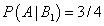 , , 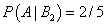 , . , .
Применяя формулу Байеса, находим апостериорные вероятности гипотез:
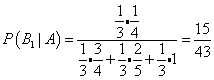 ; ;
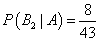 ; ; 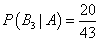 . .
|
Ответ:
|
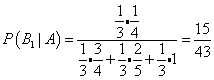 ; ;
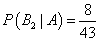 ; ;
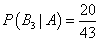 . .
|
Методические рекомендации по использованию на уроке:
|
Эту задачу можно предложить для фронтальной проверки знаний на этапе повторения пройденного материала.
|
Тема:
|
Формула Бернулли.
|
Цель обучения:
|
10.3.2.8. использовать формулу Бернули и ее следствия при решении задач.
|
Условие задачи:
|
Монета брошена 5 раз. Какова вероятность того, что герб выпадет ровно 3 раза? Сколько раз вероятнее всего выпадет герб?
|
Решение:
|
P-вероятность выпадения 3 раза герба при 5 бросках
p-вероятность выпадения герба при одном броске, она равна 1/2
n-общее количество бросков, n=5
k-количество выпадений герба, k=3
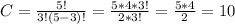
количество удачных комбинаций равно 10.
Формула Бернулли
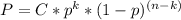
P=C*(1/2)3*(1/2)2=10*(1/2)5=10*(1/32)=10/32=0.21
|
Ответ:
|
0,21
|
Методические рекомендации по использованию на уроке:
|
Задачу можно предложить как для групповой деятельности, так и в парах на этапе закрепления формулы Бернулли.
|
9. Прикладные задачи на математическое моделирование и анализ в старших классах
Тема:
|
Прикладные задачи на применение физического и геометрического смысла производной
|
Цель обучения:
|
10.4.3.1 - решать прикладные задачи, опираясь на физический смысл производной;
|
Условие задачи:
|
Количество электричества, протекающее через проводник, начиная с момента t=0, задается формулой q=3t2+t+2 Найдите силу тока в момент времени t=3
|
Решение:
|
Сила тока есть производная q
I(t)=qꞌ(t)
I(t)= (3t2+t+2)ꞌ=6t+1
I(3)= 6*3+1=19 (A)
|
Ответ:
|
19 А
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать на алгебре (1 урок) или же на интегрированном уроке алгебры и физики. Задача предназначена для решения всеми учащимися.
|
Тема:
|
Прикладные задачи на применение физического и геометрического смысла производной.
|
Цель обучения:
|
10.4.3.1 - решать прикладные задачи, опираясь на физический смысл производной;
|
Условие задачи:
|
При извержении вулкана камни горной породы выбрасываются перпендикулярно вверх с начальной скоростью 120 м/ с. Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь?
|
Решение:
|
Вещество выбрасывается перпендикулярно вверх. Высота камня h, функция времени
h(t) = Vо t -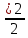 . .
Откуда следует:
h(t)= v(t)= vо–gt.
Следовательно,
0= 120-9,8t и t≈13 сек.
Тогда
h=745м, т.е. камни горной породы достигают уровня 720 м от края вулкана.
|
Ответ:
|
720 м.
|
Методические рекомендации по использованию на уроке:
|
Задачу можно предложить учащимся интересующимся физикой , повторив формулу равнозамедленного движения вверх, на уроке обощения знаний по теме «Физический и геометрический смысл производной»
|
Тема:
|
Прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Цель обучения:
|
10.4.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Условие задачи:
|
Компания изготавливает и продает изделия. Если одно изделие стоит 2000 тенге, то реализуется 1000 штук изделий. При снижении средней цены одного изделия на 50 тенге объемы реализации возрастают на 50 штук. При какой цене фирма получит максимальный доход и каково его значение?
|
Решение:
|
Пусть цена изделия снижалась k раз.
Тогда цена изделия равна 2000−50k тенге, а количество изготовленных изделий равно 1000+50k.
Тогда доход фирмы равен D(k)=(1000+50k)(2000−50k)=502(20+k)(40−k)=2500(-k2 +20k-800)
Нужно найти наибольшее значение функции D(k).
1 способ
Заметим, что графиком функции является парабола, ветви которой направлены вниз. Следовательно, наибольшее значение она принимает в вершине: k0=10.
Следовательно, максимальный доход равен
Dmax=502(20+10)(40−10)=2250000,
а цена изделия равна 2000−50⋅10=1500тг
2 способ
D(k)ꞌ=0
(-2500k2 +50 000k-2 000 000)ꞌ=-5000k+50 000 =0
K0=0
Далее аналогично
|
Ответ:
|
При цене-1500 тенге доход= 2 250 000 тенге
|
Методические рекомендации по использованию на уроке:
|
Задачу можно дать при работе в группах. Одна группа может решать через вершину параболы, другая через производную.
Задача расчитана на всех учащихся.
|
Тема:
|
Прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции.
|
Цель обучения:
|
10.4.3.3. решать прикладные задачи, связанные с нахождением наибольшего( наименьшего) значения функции.
|
Условие задачи:
|
Бак, имеющий форму прямоугольного параллелепипеда с квадратным основанием, должен вмещать 500 литров воды. При какой стороне основания площадь поверхности бака без крышки будет наименьшей?
|
Решение:
|
Пусть площадь поверхности бака будет S , Х дм – сторона квадрата, служащего основанием бака, х > 0. Бак вмещает 500 литров воды, значит, V=500 л,
V= abc ,
500= х2 h ,
h =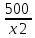 , ,
Sбок= 4хh
S = x2+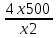
S' =2x - 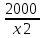 = = 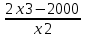
S' = 0
S' = 2x3 - 2000
2x3 – 2000 = 0
2x3 = 2000
x3 = 1000
x = 10
единственная точка экстремума и она - точка минимума.
х min = 10, Smin = S(10)
|
Ответ:
|
10
|
Методические рекомендации по использованию на уроке:
|
Задача может быть предложена на этапе самостоятельной работы в малых группах(3-4 человека) для лучшего понимания и осмысленного применения производной для решения прикладных задач.
| |
 Скачать 1.43 Mb.
Скачать 1.43 Mb.
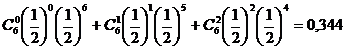
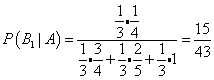 ;
;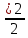 .
.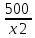 ,
, 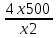
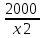 =
=