Тема:
|
Элементы математической статистики. Вариационные ряды. Анализ информации по статистической таблице, полигону и гистограмме частот
|
Цель обучения:
|
7.3.3.2 вычислять абсолютную и относительную частоты варианты;
|
Условие задачи:
|
Администрация города опубликовала данные о числе комнат в квартирах горожан. Результаты показаны в диаграмме.
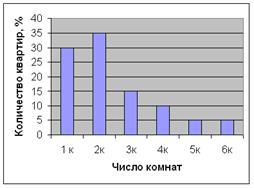
Чтобы проверить эти данные, представители независимой организации ста прохожим на улице задали вопрос: «Сколько комнат в вашей квартире?».
Ниже приведены ответы в порядке поступления:
2, 1, 1, 2, 2, 1, 1, 6, 2, 4, 1, 2, 3, 1, 2, 2, 3, 2, 2, 5, 1, 1, 2, 5, 1, 2, 2, 3, 3, 4, 2, 6, 1, 1, 6, 2, 3, 1, 2, 1, 4, 2, 1, 1, 3, 1, 2, 2, 5, 4, 2, 1, 2, 1, 1, 3, 2, 2, 3, 3, 2, 4, 1, 1, 2, 4, 1, 1, 2, «. 4, 3, 3, 6, 1, 1, 2, 4, 2, 1, 2, 1, 5, 3, 1, 2, 2, 2, 5, 1, 3, 1, 2, 4, 2, 3, 6, 3, 2, 4.
Соответствуют ли данные, полученные по выборке, приведенной диаграмме?
|
Решение:
|
Ранжируем числовые данные в порядке возрастания. В результате ранжирования ряд примет вид:
1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4
5 5 5 5 5
6 6 6 6 6 , всего опрошенных 100 человек.
Составив таблицу относительных частот.
Число комнат
|
1
|
2
|
3
|
4
|
5
|
6
|
Частота
|
30
|
35
|
15
|
10
|
5
|
5
|
Относительная частота, %
|
30
|
35
|
15
|
10
|
5
|
5
|
Построим диаграмму частот. 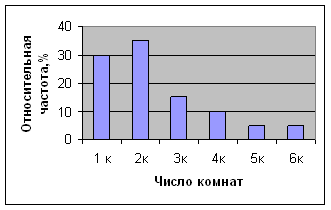
Диаграмма исходная и получившаяся совпадают, данные полученные по выборке соответствуют приведенной диаграмме.
|
Ответ:
|
соответствуют
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана на всех учащихся. Можно использовать на первых уроках по данной теме. По результатам задачи можно задать вопросы:
Реальны ли данные приведены в диаграмме
Почему 2х комнатные квартиры наиболее популярны и т.д.
Можно построить диаграмму по данным вашего класса.
|
Тема:
|
Элементы математической статистики. Вариационные ряды.
Анализ информации по статистической таблице, полигону и гистограмме частот
|
Цель обучения:
|
7.3.3.6 представлять результаты выборки в виде полигона частот;
|
Условие задачи:
|
Имеются данные о количестве студентов в 30 группах физико-математического факультета:
26
|
25
|
25
|
26
|
25
|
23
|
23
|
24
|
19
|
23
|
20
|
19
|
22
|
24
|
24
|
23
|
20
|
23
|
24
|
19
|
21
|
18
|
21
|
18
|
20
|
18
|
18
|
21
|
15
|
15
|
Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.
|
Решение:
|
Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:
|
15
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
|
2
|
4
|
2
|
4
|
3
|
1
|
5
|
4
|
3
|
2
|
Размах варьирования 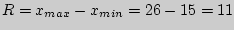 . .
Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками.
|
Ответ:
|
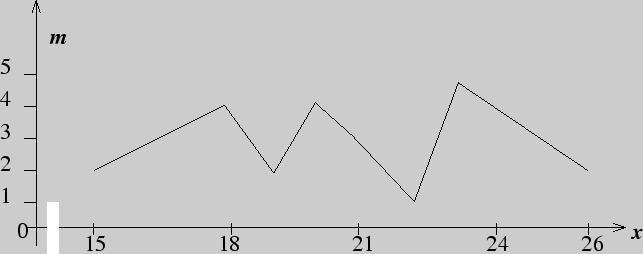
|
Методические рекомендации по использованию на уроке:
|
Задача для групповой работы;
|
Тема:
|
Элементы математической статистики. Вариационные ряды.
Анализ информации по статистической таблице, полигону и гистограмме частот
|
Цель обучения:
|
7.3.3.6 представлять результаты выборки в виде полигона частот;
|
Условие задачи:
|
Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающиеся числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
Кол-во баллов
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Кол-во шк-ов
|
2
|
3
|
2
|
4
|
12
|
10
|
8
|
9
|
Составить статистическое распределение количества школьников по количеству набранных баллов и построить полигон относительных частот.
|
Решение:
|
Пусть Х – количество набранных баллов, хі - относительные частоты.Построим таблицу относительных частот:
Х
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
хі
|
0,04
|
0,06
|
0,04
|
0,08
|
0,24
|
0,2
|
0,16
|
0,18
|
Теперь построим полигон частот, обозначив на оси ординат значения относительных частот, а на оси абсцисс – количества баллов.
Х
0,25

 0,125 0,125
   0,04 . . 0,04 . .

        13 14 15 16 17 18 19 20 хі 13 14 15 16 17 18 19 20 хі
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Можно провести групповую работу на уроке-обощения темы «Анализ информации по статистической таблице, полигону и гистограмме частот». Здесь учащиеся повторяют формулы, применяют и вычисляют объем выборки и относительную частоту.
|
Прикладные задачи на математическое моделирование и анализ
Тема:
|
Прикладные задачи на исследование квадратичных функций
|
Цель обучения:
|
8.4.2.3 использовать квадратичную функцию для решения прикладных задач
|
Условие задачи:
|
Дорога проходит под параболической аркой, как показано на рисунке. Самая высокая часть арки – 5 м. Ширина дороги – 10м, а высота – 4 м. Составьте квадратичную функцию, задающую форму арки.
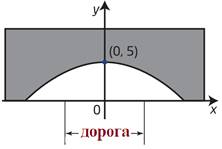
|
Решение:
|
Запишем уравнение параболы в виде 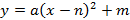 . Координаты вершины параболы (0; 5), тогда . Координаты вершины параболы (0; 5), тогда
у=а(х-0)2+5
у=ах2+5
Ширина дороги – 10м, а высота – 4 м, значит парабола проходит через точку (5;4)
4=25а+5
25а=-1
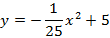
|
Ответ:
|
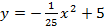 . .
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана на среднего ученика. Можно использовать для работы в группе.
|
Тема:
|
Прикладные задачи на исследование квадратичных функций.
|
Цель обучения:
|
8.4.2.3 использовать квадратичную функцию для решения прикладных задач
|
Условие задачи:
|
Вдоль наклонной доски пустили катиться снизу вверх шарик. На расстоянии 0,5 м от начала пути шарик побывал дважды: через 1 и 4 с после начала движения. Считая движение равнопеременным, определить его начальную скорость и ускорение.
|
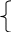 Решение: Решение:
|
Здесь t1=1с и t2=4с есть абсциссы точек пересечения параболы, задаваемой формулой X = x0 + ʋ0t – 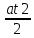 , (где ), с прямой x = l = 0,5. Другими словами, при x = l, t1 и t2 есть корни квадратного уравнения l = ʋ0t – , (где ), с прямой x = l = 0,5. Другими словами, при x = l, t1 и t2 есть корни квадратного уравнения l = ʋ0t – 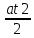 , или t2 - , или t2 - 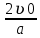 t + t + 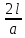 = 0. = 0.
Используя теорему Виета, получаем:
t1 + t2 = 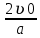 , значит а = , значит а = 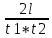 = 0.25 (м/с2) и ʋ0 = = 0.25 (м/с2) и ʋ0 = 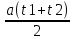 ≈0.63(м/с) ≈0.63(м/с)
t1 * t2 = 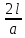
|
Ответ:
|
0.25 (м/с2), 0.63(м/с).
|
Методические рекомендации по использованию на уроке:
|
Место данной задачи на этапе закрепления изученного материала интегрированного с физикой урока.
Демонстрация задачи
Запись формулы равнопеременного движения
Решение привденного квадратнго уравнения по теореме Виета
Запись ответа
| |
 Скачать 1.43 Mb.
Скачать 1.43 Mb.