|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Тема:
|
Комплексные корни квадратного уравнения
|
Цель обучения:
|
11.1.2.4. решать квадратные уравнения на множестве комплексных чисел.
|
Условие задачи:
|
Составить квадратное уравнение, которое имеет корни z1=1−i и z2=4−5i. Решить его.
|
Решение:
|
Известно, что если z1, z2 - корни квадратного уравнения z2+bz+c=0, то указанное уравнение можно записать в виде (z−z1)(z−z2)=0. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:
(z−(1−i))(z−(4−5i))=0
Раскрываем скобки и выполняем операции над комплексными числами:
z2−(4−5i)z−(1−i)z+(1−i)(4−5i)=0
z2+z(−4+5i−1+i)+4−5i−4i+5i2=0
z2+(−5+6i)z−(1+9i)=0 - искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
D=(−5+6i)2−4⋅1⋅(−(1+9i))=−11−60i+4+36i=−7−24i
Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде√ D=a+bi. То есть
√−7−24i=a+bi⇒−7−24i=(a+bi)2⇒−7−24i=a2+2abi−b2
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений a и b:
a2−b2=−7
2ab=−24
решив которую, имеем, что a1=3, b1=−4 или a2=−3, b2=4. Рассматривая любую из полученных пар, например, первую, получаем, что√ D=3−4i, а тогда
z1= 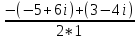 = 4−5i = 4−5i
z2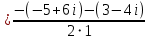 = 1−i = 1−i
Ответ. z2+(-5+6i)z-(1+9i)
|
Ответ:
|
z2+(-5+6i)z-(1+9i)
|
Методические рекомендации по использованию на уроке:
|
Эту работу можно предложить более сильным учащимся на этапе закрепления темы «Комплексные корни квадратного уравнения»
|
Тема:
|
Основная теорема алгебры
|
Цель обучения:
|
11.1.2.5. знать основную теорему алгебры и ее следствия
|
Условие задачи:
|
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и 1+i.
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены  и и 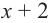 множителями многочлена множителями многочлена 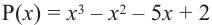 . .
|
Решение:
|
так как число 1+i является корнем многочлена, то сопряженное комплексное число 1 - i также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
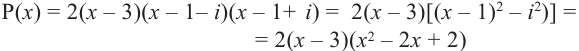
вычислим значение многочлена 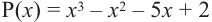 при при 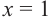 и и 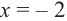 . .
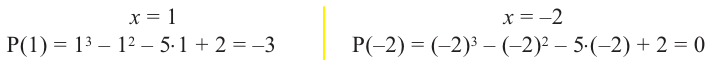
Значит, 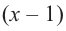 не является множителем, а не является множителем, а 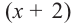 является одним из множителей данного многочлена. является одним из множителей данного многочлена.
|
Ответ:
|
2(х-3)(х2-2х+2);
(х+2).
|
Методические рекомендации по использованию на уроке:
|
Данные примеры можно предложить для парной работы на этапе обощения темы.
|
7. Методы решения уравнений и неравенств в старшей школе
Тема:
|
Решение уравнений высших степеней различными методами. Применение обобщенной теоремы Виета к многочленам третьего порядка
|
Цель обучения:
|
10.2.2.1 - применять метод разложения на множители при решении уравнений высших степеней;
|
Условие задачи:
|
Решите уравнение: 2х3 -3х2+5х-14=0
|
Решение:
|
Делители свободного члена 14: ±1, ±2, ±7
выясняем, что х=2 является корнем данного уравнения Пользуясь следствием из теоремы Безу
Разделим столбиком данное уравнение на (х-2)
2х3 -3х2+5х-14 (х-2)
2х3 –4х2 2х2 +х+7
х2 +5х
х2 -2х
7х-14
7х-14
(2х3 -3х2+5х-14)=(х-2)*(2х2 +х+7)=0
Решаем каждое уравнение отдельно:
х-2=0; х=2
2х2 +х+7=0; D=-55 <0 значит уравнение не имеет действительных корней.
|
Ответ:
|
Х=2
|
Методические рекомендации по использованию на уроке:
|
Уравнение предназначено для наработки навыков решения уравнений высших степеней разложением на множители способом деления столбиком. Задание можно использовать на первых уроках при объяснении материала или же при работе в группах, дав учащимся задание – решить разными способами.
|
Тема:
|
Решение уравнений высших степеней различными методами. Применение обобщенной теоремы Виета к многочленам третьего порядка
|
Цель обучения:
|
10.2.2.1 - применять метод разложение на множители при решении уравнений высших степеней;
|
Условие задачи:
|
x⁴-5x³-16x²+100x-80=0
|
Решение:
|
x⁴-5x³-20x²+4x²+100-80=0
x²(x²-20)-5x(x²-20)+4(x²-20)=0
(x²-5x+4)(x²-20)=0
x²-5x+4=0 или x²-20=0
D=25-16=9 x²=20
x1=(5+3)÷2=4x=±√20
x2=(5-3)÷2=-1
|
Ответ:
|
-√20; -1; 1; √20.
|
Методические рекомендации по использованию на уроке:
|
Рассчитана для парной работы;
Применить для закрепления материала по данной темы;
|
Тема:
|
Методы решения иррациональных уравнений и неравенств
|
Цель обучения:
|
11.2.2.3 - уметь решать иррациональные уравнения методом замены переменной
|
Условие задачи:
|

|
Решение:
|

|
Ответ:
|
Х=59049
|
Методические рекомендации по использованию на уроке:
|
Данное уравнение можно дать учащимся уровня АиВ, на этапе закрепления материала, для самостоятельного решения или в качестве домашнего задания.
|
Тема:
|
Методы решения иррациональных уравнений и неравенств
|
Цель обучения:
|
11.2.2.3 - уметь решать иррациональные уравнения методом замены переменной
|
Условие задачи:
|
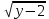 =7-y =7-y
|
Решение:
|
t=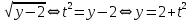
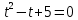 ⇔ ⇔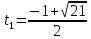 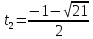
Условию t > 0 удовлетворяет лишь число t1. Поэтому обратная замена:
y=2+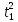 =2+( =2+(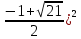 = =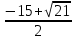
|
Ответ:
|
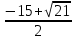
|
Методические рекомендации
|
Задачу можно дать после объяснения материала, для всех учащихся или в качестве домашнего задания.
|
Тема:
|
Методы решения иррациональных уравнений и неравенств
|
Цель обучения:
|
11.2.2.2.уметь решать ирраиональные уравнения методом возведения обеих частей уравнения в n-ю степень.
|
Условие задачи:
|
Решить уравнение = + 2 .
Решить уравнение - = 3.
|
Решение:
|
Нахождение ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе части уравнения в квадрат:
x3 + 4x - 1 - 8 = x3 - 1 + 4  + 4x; + 4x;
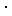 =0; =0;
x1=1; x2=0.
Произведя проверку устанавливаем, что x2=0 лишний корень.
Уединив первый радикал, получаем уравнение
= + 3, равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x2 + 5x + 2 = x2 - 3x + 3 + 6 , равносильное уравнению
4x - 5 = 3 (*). Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x2 - 40x + 25 = 9(x2 - Зх + 3), или
7x2 - 13x - 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2 = - не удовлетворяет.
|
Ответ:
|
x1=1.
x1 = 2
|
Методические рекомендации по использованию на уроке
|
Эти уравнения можно предложить более сильным учащимся на уроке решения иррациональных уравнений различными методами.
|
Тема:
|
Методы решения тригонометрических уравнений и неравенств
|
Цель обучения:
|
10.3.2.1.знать определения и свойства тригонометрических функций.
|
Условие задачи:
|
Решить уравнение cosx+sin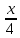 = 2 = 2
|
Решение:
|
Метод применения свойств функций
Так как функции cosx и sin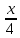 имеют наибольшее значение, равное 1, то их сумма равна 2, если cosx=1 и sin имеют наибольшее значение, равное 1, то их сумма равна 2, если cosx=1 и sin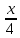 =1, одновременно, то есть =1, одновременно, то есть
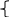 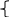
cosx=1; x=2πk, k∈Z;
sin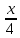 =1.⇔ x=2π+8πm, m∈Z. ⇔x=2π+8πn, n∈Z =1.⇔ x=2π+8πm, m∈Z. ⇔x=2π+8πn, n∈Z
|
Ответ:
|
x=2π+8πn, n∈Z
|
Методические рекомендации по использованию на уроке:
|
Эти уравнения можно предложить учащимся на уроке изучения свойств тригонометрических функций сразу после объяснения темы на этапе закрепления в группах.
| |
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.