5.Решение задач стереометрии
Тема:
|
Способы решения задач на нахождение площади боковой и полной поверхности пространственных фигур
|
Цель обучения:
|
11.3.1 - выводить формулы площади боковой и полной поверхности призмы и применять их при решении задач;
|
Условие задачи:
|
Сколько штук досок размером 100 мм на 2500 мм потребуется на обшивку крыши и потолка сарая, если длина крыши 4 м, ширина 3 м, а высота 2 м? Крыша имеет форму прямой треугольной призмы, в основании которой равнобедренный треугольник.

|
Решение:
|
1) Площадь одной доски = 0,1 м * 2,5 м = 0,25 м2
2) поверхность крыши, необходимая для обшивки есть площадь боковой поверхности призмы:
 Найдем длину боковой стороны основания призмы Найдем длину боковой стороны основания призмы
2
3
По теореме Пифагора l=(1,5)2 +22 =2,5 м
S потолка: 4*3 = 12 м2
S боковой части: 2,5*4=10м2
S боковой поверхности: 12+2*10=32м2
3) 32:0,25=128 (штук)
|
Ответ:
|
128 штук
|
Методические рекомендации по использованию на уроке:
|
Задачу можно решать на первых уроках после объяснения материала или же дать для самостоятельного решения (домашней работы). Прикладной характер может вызвать интерес к изучению заданной темы. Рассчитана на всех учащихся.
|
Тема:
|
Способы решения задач на нахождение площади боковой и полной поверхности пространственных фигур. Использование графических редакторов при решении задач на сечение многогранника плоскостью.
|
Цель обучения:
|
11.3.3 - решать задачи на нахождение элементов многогранников;
|
Условие задачи:
|
Основание пирамиды — прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
|
Решение:
|
 Так как SA = SB = SC = SD, то прямоугольные треугольники ASO, BSO, CSO и DSO равны по гипотенузе и общему катету SO. Так как SA = SB = SC = SD, то прямоугольные треугольники ASO, BSO, CSO и DSO равны по гипотенузе и общему катету SO.
Тогда AO = BO = CO = DO, а значит, точка О является точкой пересечения AC и BD. В ΔABD:

в ΔSOD по теореме Пифагора:
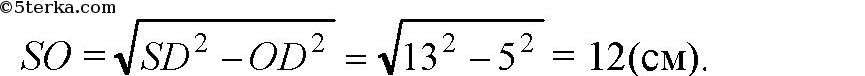
|
Ответ:
|
12см.
|
Методические рекомендации по использованию на уроке:
|
Задача для большинства;
Использовать задачу можно в суммативных работах;
|
Тема:
|
Способы решения задач на нахождение площади боковой и полной поверхности пространственных фигур.
|
Цель обучения:
|
11.3.3 - решать задачи на нахождение элементов многогранников;
|
Условие задачи:
|
В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 600. Найдите боковое ребро пирамиды.
|
Решение:
|

Пирамида правильная, значит в основании квадрат, боковые грани - равные равнобедренные треугольники, высота проецируется в точку пересечения диагоналей квадрата.
Пусть Н - середина CD. Тогда SH - медиана и высота равнобедренного треугольника SCD, ОН - медиана и высота равнобедренного треугольника OCD.
SH⊥CD, OH⊥CD, ⇒∠SHO = 60° - линейный угол двугранного угла между боковой гранью и основанием.
ОН = AD/2 = 6/2 = 3 cм как средняя линия ΔACD.
ΔSOH: ∠SOH = 90°, cos∠SHO = OH/SH
SH = OH / cos∠SHO = 3 / (1/2) = 6 см
ΔSHC: ∠SHC = 90°, SH = 6 см, HС = 3 см, по теореме Пифагора:
SC = √(SH²+ HC²) = √(36 + 9) = √45 = 3√5 см
|
Ответ:
|
SC=3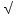 5 5
|
Методические рекомендации по использованию на уроке:
|
Предложить сильным учащимся на этапе закрепления.
|
Тема:
|
Методы решения задач на нахождение элементов тел вращения и объемов пространственных фигур.
|
Цель обучения:
|
11.3.4 - выводить формулы площади боковой и полной поверхности цилиндра и применять их при решении задач;
|
Условие задачи:
|
Сколько жести потребуется для изготовления ведра цилиндрической формы, с радиусом основания - 15см, высотой 50 см. Учесть, что на заклепки уходит 10% материала?
|
Решение:
|
 

Площадь боковой поверхности цилиндра представляет из себя прямоугольник с шириной 50см, а длина прямоугольника – это длина окружности основания.
Значит чтобы найти площадь боковой поверхности нужно ширину умножить на длину окружности - 2πR
S=2πRH S=2π*15*50=1500πcm2
Учитывая, что на заклепки уходит 10% жести, то общее количество:
S=1,1*Sбок=1,1*1500π ≈ 5181(см2).
|
Ответ:
|
5181 см2 = 0,52м2
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать для самостоятельного вывода формулы площади боковой поверхности цилиндра. Прикладной характер может вызвать интерес к изучению заданной темы. Рассчитана на всех учащихся.
|
Тема:
|
Методы решения задач на нахождение элементов тел вращения и объемов пространственных фигур.
|
Цель обучения:
|
1.3.4 - выводить формулы площади боковой и полной поверхности цилиндра и применять их при решении задач;
|
Условие задачи:
|
Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна . Найти радиус основания и высоту.

|
Решение:
|
Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна . Найти радиус основания и высоту.
Решение. По формуле имеем: 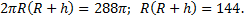
По условию, , имеем:

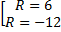 . .
Так как радиус положителен, то 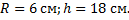
Ответ: . .
|
Ответ:
|
Ответ: . .
|
Методические рекомендации по использованию на уроке:
|
Использовать для большинства;
|
Тема:
|
Методы решения задач на нахождение элементов тел вращения и объемов пространственных фигур
|
Цель обучения:
|
11.3.5 - решать задачи на нахождение элементов тел вращения (цилиндра, конуса, усеченного конуса, шара);
|
Условие задачи:
|
Даны два конуса. Радиус второго конуса в 3 раза больше радиуса первого конуса, а высота второго конуса в 6 раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен 18.
|
Решение:
|
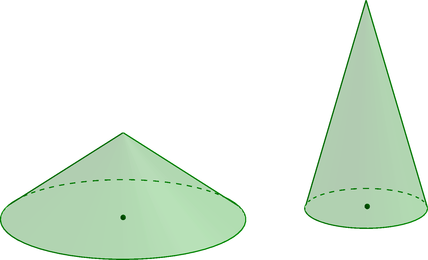
Объем конуса с высотой h и радиусом основания R вычисляется по формуле V=13πR2h. Следовательно, объем первого конуса относится к объему второго конуса как
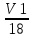 = = = =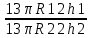 = ( = (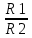 )2⋅ )2⋅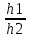
Так как радиус второго в 3 раза больше радиуса первого, то R2=3R1. Так как высота второго в 6 раз меньше высоты первого, то h1=6h2. Следовательно, 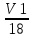 = ( = ( 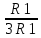 )2 ⋅ )2 ⋅  = = ⋅6 = ⋅6 = ⇒ V1 = ⇒ V1 = ⋅18 = 12. ⋅18 = 12.
|
Ответ:
|
12
|
Методические рекомендации по использованию на уроке:
|
Можно провести групповую работу после изучения темы.
|
Тема:
|
Решение задач на комбинации многогранников и тел вращения.
|
Цель обучения:
|
11.3.18 - решать задачи практического содержания на комбинации геометрических тел
|
Условие задачи:
|
 
Диаметр сферы Нур-Алем равен 80м. Здание Дворца мира и согласия имеет форму правильной пирамиды, сторона основания и высота которой равны 61,8 м. Можно ли поместить пирамиду в сферу?
|
Решение:
|
    

 
Проверим войдет ли основание пирамиды в сферу?

 
d = a√2
d=61,8√2=87,4 это диаметр окружности описанной вокруг основания пирамиды.
80<87,4
Вывод: нельзя поместить данную пирамиду в данную сферу.
|
Ответ:
|
Нельзя
|
Методические рекомендации по использованию на уроке:
|
Данную задачу можно использовать на первом уроке по теме Сечения сферы. Рассчитана на всех учащихся.
После решения можно задать вопрос: А если бы основание помещалось в сферу, что нужно найти следующим этапом?
|
Тема:
|
Решение задач на комбинации многогранников и тел вращения.
|
Цель обучения:
|
11.3.18 - решать задачи практического содержания на комбинации геометрических тел
|
Условие задачи:
|
Вычислить вес сена в стоге, если один кубический метр сена весит 84 кг.
|
Решение:
| 
Vц. =  R2H = R2H =  224 = 16 224 = 16 (П (П 3) 3)
Vк. = 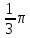 221 = 221 = 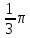 221 = 221 =   = = = = 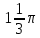
Vс. = Vц.+ Vк. = 16 + + 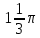 = =
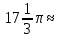 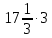 = 51 + 1 = 52 м3 = 51 + 1 = 52 м3
m = 54 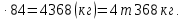
|
Ответ:
|
Ответ: 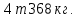
|
Методические рекомендации по использованию на уроке:
|
Использовать задачу в групповой работе;
| |
 Скачать 1.43 Mb.
Скачать 1.43 Mb.