|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
4. Решение задач планиметрии
Тема:
|
Решение треугольников. Практические задачи геометрии
|
Цель обучения:
|
9.1.3.6 знать и применять теорему косинусов;
|
Условие задачи:
|
Одна из сторон треугольника равна 3 см, а две другие стороны относятся как √2 :1 . Найти величину угла между этими двумя сторонами, если периметр треугольника равен 6 3 √2 см.
|
Решение:
|
Поскольку отношение неизвестных сторон равно √2 :1 , обозначим их через x√2 и x.
Тогда, записывая периметр треугольника, получим уравнение: 3 x x√2 6 3√2 . Отсюда x1√2 31√2 , то есть x 3 .
Значит, неизвестные стороны треугольника равны 3 и 3√2 . Если угол между ними обозначить через , то по следствию 1 из теоремы косинусов получим:
cos 
следовательно угол равен 45º
|
Ответ:
|
α=45º
|
Методические рекомендации по использованию на уроке:
|
Данная задача рекомендована для решения учащимся уровня А,В. Можно давать как дифференцированное задание при делении на одноуровневые группы.
|
Тема:
|
Решение треугольников. Практические задачи геометрии.
|
Цель обучения:
|
9.1.3.10 применять теоремы синусов и косинусов для решения треугольников
|
Условие задачи:
|
В Задача № 1.

5 7 Найдите сторону АС
60⁰
A х С
|
Решение:
|
I способ (с использование теоремы косинусов)
Пусть АС = х
По теореме косинусов ВС2 = АС2 + АВ2 – 2 АС ∙ АВ ∙ cos 60⁰
72 = 52 + x2 – 2 ∙ 5 ∙ x ∙ 
x2 – 5x – 24 = 0
x1 = 8; x2 = - 3 (не уд. усл. задачи)
Ответ: АС = 8
II способ (с использование теоремы синусов)
Пусть АС = х
По теореме синусов  ; ; 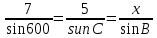 ; ;
Sin C = 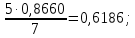 ∠C = 38⁰ 14´ ∠C = 38⁰ 14´
∠B = 180⁰ - 60⁰ - 38⁰ 14´ = 81⁰46´; x =  = = 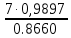 ≈ 8 ≈ 8
Ответ: АС = 8
|
Ответ:
|
АС=8
|
Методические рекомендации по использованию на уроке:
|
Задачу дать на итоговых уроках. Можно дать в группах для решения различными способами. Работа в парах;
|
Тема:
|
Решение треугольников. Практические задачи геометрии.
|
Цель обучения:
|
9.1.3.6 знать и применять теорему косинусов;
|
Условие задачи:
|
Два парохода начинают движение одновременно из одного и того же пункта и двигаются равномерно по прямым пересекающимся под углом 600. Скорость первого 40км/ч, второго – 30км/ч. Вычислите, на каком расстоянии друг от друга будут находиться пароходы через 3 часа?
|
Решение:
|
 V1= 40 км/ч s1 =120 км V1= 40 км/ч s1 =120 км
 V2 = 30км/ч s2=90 км В V2 = 30км/ч s2=90 км В
По теореме косинусов:
 ВС2 = АС2 + АВ2 – 2АС АВ А ВС2 = АС2 + АВ2 – 2АС АВ А
ВС2 =1202 + 902 – 2*120*90
ВС2 =14400 + 8100 – 10800 С
ВС2 =11700; ВС = 
|
Ответ:
|
108 км
|
Методические рекомендации по использованию на уроке:
|
Работа в парах. Применять на этапе закрепления сильным ученикам группы С или на уроке решения практических задач по геометрии дать для самостоятельной работы в парах. Обучающиеся повторяют основную формулу движения и вычисляют пройденный путь при известных скорости и времени. Затем применяют теорему косинусов.
|
Тема:
|
Векторы на плоскости. Применение векторов в решении геометрических задач
|
Цель обучения:
|
9.1.4.19 применять векторы к решению задач
|
Условие задачи:
|
Доказать, что линия, соединяющая середины диагоналей произвольной трапеции параллельна основаниям этой трапеции и равна их полуразности.
|
Решение:
|
 
Рассмотрим вектор MN. Используя правило многоугольника для сложения векторов, с одной стороны, получим
       
MN=MA+AD+DN С другой стороны MN=MC+CB+BN Сложим два последних равенства:
      
2MN=MA+AD+DN+MC+CB+BN Так как MN - отрезок, соединяющий середины диагоналей, то
   
MA+MC=0, DN+BN=0 Тогда получим
     
  2MN=AD+CB=AD−BC. То есть MN=(AD−BC):2 Так как и 2MN=AD+CB=AD−BC. То есть MN=(AD−BC):2 Так как и

   AD и BC сонаправлены, то MN||AD. Из этого получаем, что MN=(AD−BC):2 и MN||AD AD и BC сонаправлены, то MN||AD. Из этого получаем, что MN=(AD−BC):2 и MN||AD
|
Ответ:
|
MN=(AD−BC):2 и MN||AD
|
Методические рекомендации по использованию на уроке:
|
Задача на доказательство расчитана на учащихся уровня А.
Можно дать в качестве домашнего задания или как дифференцированное задание на уроке.
|
Тема:
|
Векторы на плоскости. Применение векторов в решении геометрических задач.
|
Цель обучения:
|
9.1.4.6 находить скалярное произведение векторов;
|
Условие задачи:
|
Найти скалярное произведение векторов a = (4; -3; 1) и b = (5; -2; -3)
|
Решение:
|
Скалярным произведением векторов a(x1;y1;z1) и b(x2;y2;z2), заданных своими координатам, находится по формуле:
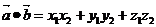
По формуле находим a·b = 4·5 + (-3)·(-2) + 1·(-3) = 23. Поскольку 23≠0, то данные вектора не перпендикулярны
|
Ответ:
|
23
|
Методические рекомендации по использованию на уроке:
|
Задание для большинства. Использовать как тренировочное задание для наработки навыков.
|
Тема:
|
Векторы на плоскости. Применение векторов в решении геометрических задач.
|
Цель обучения:
|
9.1.4.19 применять векторы к решению задач
|
Условие задачи:
|
Парашютист спускался со скоростью м/с. Ветром его начинает сносить в сторону со скоростью м/с. Какова его реальная скорость ? Под каким углом к вертикали спускается парашютист?
|
Решение:
|
Скорость – векторная величина. Т. к. парашютист имеет две скорости в различных направлениях, то результирующая (истинная скорость) находится как векторная сумма первых двух:
 Рис.1 Рис.1
Найдем ее, используя правило параллелограмма (в нашем случае параллелограмм – это прямоугольник:
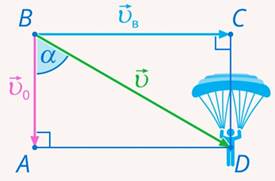
Рис.2 Прямоугольник
Значение реальной скорости – это длина вектора, т. е. диагонали прямоугольника:

Ее можно найти, используя теорему Пифагора:
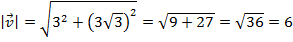 м/с м/с
Тангенс искомого угла между вертикалью и реальной скоростью равен, по определению, отношению противолежащего катета к прилежащему:

Острый угол, который соответствует такому тангенсу, равен
|
Ответ:
|
6 м/с, 600
|
Методические рекомендации по использованию на уроке:
|
Эту задачу можно предложить учащимся группы В и С после изучения темы «Сложение векторов» на этапе закрепления. Или же выдать как домашнее задание в конце главы.
|
Тема:
|
Преобразования плоскости. Методы решения задач с применением преобразований плоскости
|
Цель обучения:
|
9.1.4.10 решать задачи с применением преобразований плоскости;
|
Условие задачи:
|
На прямой 2x + y + 3 = 0 найти точку, которая при центральной симметрии с центром в начале координат переходит в точку, принадлежащую прямой x – y – 3 = 0
|
Решение:
|
Запишем уравнение прямой в виде:
у= -2х-3
При центральной симметрии прямая переходит в параллельную ей прямую. Значит угловой коэффициент данной прямой и прямой ей симметричной равны (-2)
Рассмотрим точку А(0;-3) лежащую на оси ОУ и принадлежащую данной прямой. Ей симметричная точка относительно начала координат будет точка В(0;3) она лежит на симметричной прямой. Значит уравнение симметричной прямой у=-2х+3.
Найдем точку пересечения прямых у=-2х+3 и у=х-3
Приравняв их получим х=2, подставив в любое уравнение найдем у. Значит точка пересечения С(2,-1).
Точка ей симметричная относительно начала координат и будет искомая точка М(-2;1).
  
|
Ответ:
|
М(-2;1)
|
Методические рекомендации по использованию на уроке:
|
Задачу можно дать для работы в группе. Учащимся уровня А,В решить аналитически, учащимся уровня С можно дать решить графически или используя GeoGebra.
|
Тема:
|
Преобразования плоскости. Методы решения задач с применением преобразований плоскости
|
Цель обучения:
|
9.1.4.10 решать задачи с применением преобразований плоскости;
|
Условие задачи:
|
В каком месте надо построить мост MN через реку, разделяющую деревни А и В, так, чтобы дорога AMNB между деревнями была самой короткой? (Берега реки считаются параллельными, а мост перпендикулярным к ним)
|
Решение:
|
При решении задачи используем параллельный перенос. Мост MN следует построить так, чтобы точка N была точкой пересечения прямой А1В1 и ближайшего к деревне В берега реки, где А1- точка, в которую переходит точка А при параллельном переносе на вектор 
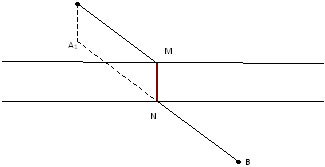
|
Ответ:
|
Отрезок MN
|
Методические рекомендации по использованию на уроке:
|
Создать группы для поисково-исследовательской работы над решением практической задачей по построению моста.
Предложить презентовать свои работы и защитить ее. Самую лучшую отметить грамотой или дипломом.
| |
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.