|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Тема:
|
Решение логарифмических, показательных уравнений и неравенств
|
Цель обучения:
|
11.2.2.6 - знать и применять методы решения показательных уравнений
|
Условие задачи:
|
Вкладчик положил в Халык банк 100 000 тенге под ставку 14 % годовых. Через сколько лет его вклад удвоится? (используется формула сложных процентов)
|
Решение:
|
Формула сложного процента:
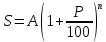
где: А- начальная сумма вклада
Р- годовая процентная ставка
n- срок хранения вклада
S- накопительная сумма вклада
Значит 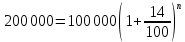
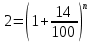
Решаем это уравнение с помощью логарифма 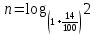
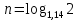 . Перейдем к основанию 10 и с помощью калькулятора посчитаем: . Перейдем к основанию 10 и с помощью калькулятора посчитаем: 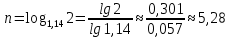
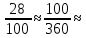 3 месяца 3 месяца
Делаем вывод, что сумма вклада удвоится через 5 лет и 3 месяца
|
Ответ:
|
Сумма вклада удвоится через 5 лет и 3 месяца
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать для иллюстрации практического применения показательных уравнений. Предназначена для всех учащихся.
|
Тема:
|
Решение систем логарифмических, показательных уравнений и неравенств
|
Цель обучения:
|
11.2.2.6 - знать и применять методы решения показательных уравнений
|
Условие задачи:
|
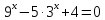
|
Решение:
|
Упростим показательное уравнение
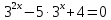
применим метод введения новой переменной
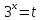
пусть данное уравнение можно записать в виде
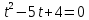
решая это квадратное уравнение, получаем
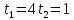
теперь задача сводится к решению совокупности уравнений
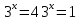
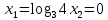
|
Ответ:
|
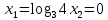
|
Методические рекомендации по использованию на уроке:
|
Данное уравнение можно дать учащимся на этапе закрепления материала, для самостоятельного решения или в качестве домашнего задания.
|
Тема:
|
Решение систем логарифмических, показательных уравнений.
|
Цель обучения:
|
11.2.2.8. знать и применять методы решения логарифмических уравнений
|
Условие задачи:
|
Иван и Маша решали задачу: некоторое заданное трехзначное число прологарифмировать по основанию 2, из полученного числа вычесть некоторое заданное натуральное число, а затем разность разделить на то же самое натуральное число.Иван перепутал и в первом действии прологарифмировал по основанию 3,а Маша посчитала правильно. Когда они сравнили свои результаты, оказалось, что полученные ими числа взаимно обратны. Найти исходное трехзначное число.
|
Решение:
|
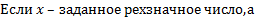 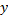 - натуральное число, вычитаемое во втором действии, тогда: - натуральное число, вычитаемое во втором действии, тогда:
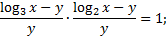
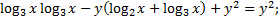
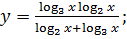
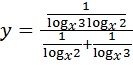 ; ;
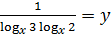 ; ;
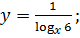
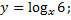

|
Ответ:
|
216
|
Методические рекомендации по использованию на уроке:
|
Эту задачу я бы предложила творческой группе учащихся, предпочитающих сложные задачи для подготовки к ЕНТ.
|
8. Статистика и теория вероятностей в старших классах
Тема:
|
Вероятность события и ее свойства. Правила сложения и умножения вероятностей.
|
Цель обучения:
|
10.3.2.3 - понимать и применять правила сложения вероятностей
* P(A + B) = P(A) + P(B)
* P(A +B) = P(A) + P(B) – P(A ∙ B);
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);
|
Условие задачи:
|
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: а) только один из стрелков; б) хотя бы один стрелок.
|
Решение:
|
Рассмотрим события:
первый стрелок попал; ;
первый стрелок промахнулся; ;
второй стрелок попал; ;
второй стрелок промахнулся; .
а) Событие B попал только один стрелок, используя алгебру событий, можно представить в виде
.
Тогда по теореме сложения вероятностей несовместных и умножения независимых событий имеем:
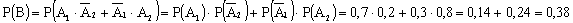
б) Событие C попал хотя бы один стрелок можно представить как сумму двух несовместных событий: B — попал только один стрелок и D- попали оба стрелка
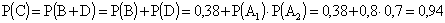 . .
Однако вероятность события C можно найти другим способом. Рассмотрим событие оба промахнулись,
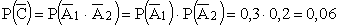 . .
Тогда .
|
Ответ:
|
а) 0,38 б)0,94
|
Методические рекомендации по использованию на уроке:
|
Задача дается после прохождения сложения и умножения вероятностей, для обобщения этих тем. Использовать задачу можно при работе в группах, так как учащиеся могут представить разные способы решения. Расчитана на учащихся уровня АиВ, учащиеся уровня С могут производить расчеты по уже готовым формулам.
|
Тема:
|
Вероятность события и ее свойства. Правила сложения и умножения вероятностей.
|
Цель обучения:
|
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);
|
Условие задачи:
|
Из коробки, содержащей 3 белых и 5 чёрных шаров, наугад взяли 3 шара. Какова вероятность того, что все 3 шара оказались чёрного цвета?
|
Решение:
|
Когда берётся первый шар, то в коробке находится 8 шаров, из которых 5 шаров имеют чёрный цвет.
Следовательно, P(A1) = 5/8. Когда берётся второй шар при условии, что событие A1 уже произошло, то в коробке находится 7 шаров, причём чёрных шаров осталось 4 (один уже был взят). Значит Р(А2 ⁄А1) = 4/7. После извлечения второго шара в коробке осталось 6 шаров, в том числе 3 чёрных. Таким образом, Р(А3 ⁄ A1A2) = 3/6=1/2.
Искомая вероятность равна: P(A1A2A3) = ( 1/2) ∙(4/7) ∙(5/8) = 5/28.
|
Ответ:
|
5/28
|
Методические рекомендации по использованию на уроке:
|
Задача для большинства;
Для закрепления материала;
|
Тема:
|
Задачи на нахождение вероятностей с применением формулы комбинаторики. Применение бинома Ньютона для приближённых вычислений.
|
Цель обучения:
|
10.3.1.2 - применять формулы для вычисления перестановок, сочетаний, размещений без повторений
|
Условие задачи:
|
В бригаде из 20 рабочих требуется выбрать троих для направления в командировку. Сколько существует вариантов выбора?
|
Решение:
|
Последовательность выбора в данном случае не имеет значения. Значит число вариантов выбора равно числу сочетаний из 20 объектов (рабочих) по 3:
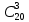 = 20! ⁄ (3!17!) = 20∙19∙18 ⁄ 6 = 1140. = 20! ⁄ (3!17!) = 20∙19∙18 ⁄ 6 = 1140.
Для более сложных задач при подсчёте числа комбинаций следует действовать в соответствии с основным правилом комбинаторики.
|
Ответ:
|
1140
|
Методические рекомендации по использованию на уроке:
|
Задача для большинства;
Применяется для наработки навыков решения.
|
Тема:
|
Задачи на нахождение вероятностей с применением формулы комбинаторики. Применение бинома Ньютона для приближённых вычислений.
|
Цель обучения:
|
10.3.1.5 - применять Бином Ньютона для приближённых вычислений (с натуральным показателем)
|
Условие задачи:
|
Часто в расчетных задачах необходимо возвести число π в некоторую степень. Вычислите π4 с точностью до 0,1 используя формулу бинома Ньютона.
(1 + 𝑥) 𝑛 = 1 + 𝑛𝑥 + 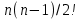 *𝑥 2 + 𝑛(𝑛 − 1)(𝑛 − 2) /3!* 𝑥 3 + ⋯ *𝑥 2 + 𝑛(𝑛 − 1)(𝑛 − 2) /3!* 𝑥 3 + ⋯
0,14/3 примите ≈0,047
|
Решение:
|
Решение: 3,144 = (3+ 0,14)4 = (3(1+0,14/3))4 = 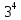 (1 + 0,05) 4 (1 + 0,05) 4
=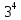 ( (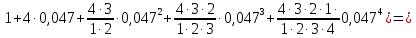
Оценим третье слагаемое:
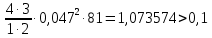
оценим четвертое слагаемое
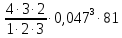 ≈0,0336< 0,1 ≈0,0336< 0,1
Следовательно, начиная с четвертого слагаемые суммы можно не рассматривать:
81(1+0,188+0,013254)=97,301574
|
Ответ:
|
97,301574
|
Методические рекомендации по использованию на уроке:
|
Задачу можно дать в качестве домашнего задания после объяснения материала. Затем возвести 3,14 в 4 степень с помощью калькулятора. И попросить сделать выводы почему появилась разница в ответах и на сколько? И дать задание найти более точный ответ.
|
Тема:
|
Задачи на нахождение вероятности с применением формул комбинаторики.
|
Цель обучения:
|
10.3.1.4. решать задачи на нахождение вероятностей, применяя формулы комбинаторики.
|
Условие задачи:
|
В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?
|
Решение:
|
Прежде всего, обратить внимание на то, что по логике условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы
(в этом случае их можно, например, пронумеровать).
В задаче речь идёт о выборке из 4 деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:
В похожей ситуации можно использовать следующий приём: в знаменателе выбираем наибольший факториал (в данном случае ) и сокращаем на него дробь. Для этого числитель следует представить в виде . Распишем очень подробно:
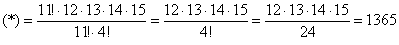 способами можно взять 4 детали из ящика. способами можно взять 4 детали из ящика.
Ещё раз: что это значит? Это значит, что из набора 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетания 4 деталей. То есть, каждая такая комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью.
|
Ответ:
|
1365 способами
|
Методические рекомендации по использованию на уроке:
|
Задача на первый взляд несложная, поэтому, определив формулу для решения задачи, вычислить ответ. Можно решать такие задачи на этапе закрепления нового материала.
| |
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.