Тема:
|
Решение текстовых задач с помощью уравнений и неравенств
|
Цель обучения:
|
6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений;
|
Условие задачи:
|
Рукопись набрали три оператора. Первый набрал 20% рукописи, остальное- второй и третий. Отношение количества страниц, набранных вторым оператором к количеству страниц, набранных третьим, равно 2/3. Третий оператор набрал на 24 страниц больше, чем второй.
Сколько страниц в рукописи?
|
Решение:
|
Записать краткую запись;
Ввести обозначения;
Составить уравнение и решить его;
Записать пропорцию и применить ее основное свойство;
Найти число по его процентам и записать ответ.
1оператор – 20%
2 оператор + 3 оператор – 80%
2оп./3оп. = 2/3
3 оп. на 24 стр больше, чем 2 оп.
Ск-ко стр в рукописи?
По условию задачи введем следующие обозначения: 2х- число страниц, набранных 2-м оператором; 3х – третьим.
Тогда
3х – 2х = 24
х = 24
значит 2х = 48, 3х = 72.
2-й оператор набрал 48 страниц, 3-й – 72 страницы. Вместе 48+72 = 120 страниц.
Теперь находим общее число страниц по его процентам. Применим основное свойство пропорции:
120 стр – 80%
? стр – 100%
Найдем неизвестный средний член пропорции
? = 120*100/80 ? = 150
|
Ответ:
|
В рукописи 150 страниц
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать для работы в группе, работая по алгоритму. Рассчитана на всех учащихся
|
Тема:
|
Решение текстовых задач с помощью линейных уравнений
|
Цель обучения:
|
6.5.1.7 решать текстовые задачи с помощью составления систем линейных уравнений;
|
Условие задачи:
|
Окружность с центром О разделена на четыре угла с разными градусными мерами. Градусная мера первого угла равна а0, второго b0, третьего c0, четвертого d0.
Cумма углов:
Первого и второго равна 1400;
Первого и третьего равна 1600;
Первого и четвертого равна 1800.
Найдите градусную меру каждого угла.
|
  Решение: Решение:
|
І – а0
ІІ - b0
ІІІ - c0
ІV - d0
а0, b0,c0,d0 -?
По условию задачи составим cистему из четырех линейных уравнений:
а0 + b0 = 1400 (1)
а0 + c0 = 1600 (2)
а0 + d0= 1800 (3)
b0 + c0 = 1800 (4)
Для решения этой системы применим метод алгебраического сложения. Из (2) - (1) и получим новую систему из трех линейных уравнений:
c0- b0 = 200 (1)
c0+ b0 = 1800 (2)
а0 + d0= 1800 (3)
Еще раз применим метод алгебраического сложения. К (1) + (2) и получим систему из двух линейных уравнений:
 2 c0 = 2000 2 c0 = 2000
а0 + d0= 1800
откуда вычислим градусную величину угла c0, разделив обе части первого уравнения на коэффициент 2.
c0=1000.
Из первого c0- b0 = 200 (1)
или второго c0+ b0 = 1800 (2)
уравнения второй системы находим градусную величину угла b0.
b0 = 1800 - 1000
b0 = 800.
Следующим шагом найдем градусную величину угла а0 из уравнения первой системы
а0 + b0 = 1400 (1).
а0 = 1400 - 800
а0 = 600.
Из а0 + d0= 1800 (3) найдем d0.
а0 + d0= 1800
d0= 1800 - 600
d0= 1200
|
Ответ:
|
а0 = 600, b0 = 800, c0=1000, d0= 1200
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать для работы в группе или можно дать в качестве домашнего задания. Рассчитана на среднего ученика
|
Методы решения задач по статистике и теории вероятностей в основной школе
Тема:
|
Элементы комбинаторики. Решение задач с использованием формул комбинаторики. Бином Ньютона и его свойства.
|
Цель обучения:
|
9.3.1.5 Решать задачи, применяя формулы комбинаторики, для вычисления числа перестановок, размещений, сочетания без повторений
|
Условие задачи:
|
Сколько можно записать четырехзначных чисел, используя без повторения все 10 цифр?
|
Решение:
|
1) 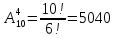
2) т.к. есть среди чисел 0, который не может стоять впереди, поэтому надо еще найти

3) 
|
Ответ:
|
4536 чисел
|
Методические рекомендации по использованию на уроке:
|
Задача рассчитана на всех учащихся. Можно решать на Проблемном уроке, дав возможность решить ее самостоятельно и сделать выводы. Или же при работе в парах.
|
Тема:
|
Элементы комбинаторики. Решение задач с использованием формул комбинаторики. Бином Ньютона и его свойства
|
Цель обучения:
|
9.3.1.6 Знать и применять формулу бинома Ньютона и его свойства
|
Условие задачи:
|
Выполнить возведение в степень: 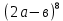
|
Решение:
|
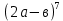 = = -7 -7 +21 +21 -35 -35 +35(2а +35(2а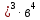 - - = =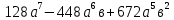 -560 -560
280
Число слагаемых на 1 больше степени
Коэффициенты находятся по треугольнику Паскаля
Коэфициенты симметричны
Если в скобке знак минус, то знаки + и – чередуются
Сумма степеней каждого слагаемого равна степени бинома
|
Ответ:
|
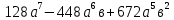 -560 -560
280
|
Методические рекомендации по использованию на уроке:
|
Задача на закрепление нового материала. Можно дать на первом уроке после объяснения материала, для самостоятельного выполнения
|
Тема:
|
Элементы комбинаторики. Решение задач с использованием формул комбинаторики.
|
Цель обучения:
|
9.3.1.1 Знать правила комбинаторики (правила суммы и произведения)
|
Условие задачи:
|
При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов?
|
Решение:
|
Каждый из 6-ти специалистов отдал по 5 карточек (всем, кроме себя). Потребовалось
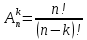 А26 = А26 = 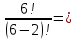 6·5 = 30 карточек. 6·5 = 30 карточек.
|
Ответ:
|
30
|
Методические рекомендации по использованию на уроке:
|
Предложить задачу на вводном уроке по теме «Размещения без повторений» для закрепления формулы. Для всех учащихся
|
Тема:
|
Методы решения задач на событие и вероятность. Применение геометрической вероятности при решении задач.
|
Цель обучения:
|
9.3.2.3 знать классическое определение вероятности и применять его для решения задач;
|
Условие задачи:
|
В классе 21 учащийся, среди них два друга — Кайрат и Самат. На уроке математики класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Кайрат и Самат окажутся в одной группе.
|
Решение:
|
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3
|
Ответ:
|
0,3
|
Методические рекомендации по использованию на уроке:
|
Задачу можно переформулировать для конкретного класса, тем самым вызвать интерес у учащихся. Использовать на начальных уроках изучения данной темы
|
Тема:
|
Методы решения задач на событие и вероятность. Применение геометрической вероятности при решении задач.
|
Цель обучения:
|
9.3.2.3 знать классическое определение вероятности и применять его для решения задач;
|
Условие задачи:
|
На листок бумаги в клетку со стороной 10мм падает кружок диаметра 2мм. Какова вероятность того, что кружок целиком попадет внутрь клетки?
|
Решение:
|
 
2
 
10

8
На рисунке заштрихована область, попадание центра кружка в которую дает возможность утверждать, что кружок не заденет ни одной из сторон квадрата. Эта область представляет собой квадрат со стороной 8мм. Значит искомая вероятность равна Р(А)= (8*8)/(10*10)=0,64
|
Ответ:
|
0,64
|
Методические рекомендации по использованию на уроке:
|
Рассчитана для большинства;
|
Тема:
|
Применение геометрической вероятности при решении задач.
|
Цель обучения:
|
9.3.2.5 Применять геометрическую вероятность при решении задач
|
Условие задачи:
|
В прямоугольник 5×45×4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
|
Решение:
|
По определению геометрической вероятности искомая вероятность равна отношению площади круга (в который точка должна попасть) к площади прямоугольника (в которой точка ставится), т.е.
P= = =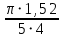 = 0,353. = 0,353.
|
Ответ:
|
0,353
|
Методические рекомендации по использованию на уроке:
|
Эту задачу можно выполнить в паре как самостоятельную работу на втором уроке на этапе повторения темы «Применение геометрической вероятности при решении задач».
| |
 Скачать 1.43 Mb.
Скачать 1.43 Mb.