|
|
ИТОГОВАЯ 2 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Тема:
|
Решение задач на комбинации многогранников и тел вращения.
|
Цель обучения:
|
11.3.18 - решать задачи практического содержания на комбинации геометрических тел
|
Условие задачи:
|
Высота конуса 8, образующая 10. Найдите радиус вписанного шара.
|
Решение:
|
Найдем радиус основания конуса r.
OC = 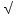 AC2 – AO2 = AC2 – AO2 =  36 = 6 36 = 6
∆AC: AC = AD =˃ AO – медиана, DC = 12
S∆ ADC = pr = p*KB, r = 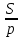

S∆ ADC =  DC * AO = DC * AO =  * 8 * 12 = 48 * 8 * 12 = 48
p=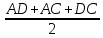 = 16 = 16
r = KB = 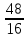 = 3 = 3
|
Ответ:
|
3
|
Методические рекомендации по использованию на уроке:
|
Эту задачу можно рассмотреть при объяснении темы.
|
6.Комплексные числа. Основная теорема алгебры
Тема:
|
Арифметические действия над комплексными числами в алгебраической форме
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме
|
Условие задачи:
|
Выполните действия:
(3+4i)+(5-2i)
6(4-3i)- 3(1+3i)
(3-5i)(3+5i)

|
Решение:
|
(3+4i)+(5-2i)= 3+4i+5-2i=8+2i
6(4-3i)- 3(1+3i)=24-18i-3-9i=21-27i
(3-5i)(3+5i)=9-(5i)2 =9-25i2 =9+25=34
 = =
|
Ответ:
|
8+2i, 2) 21-27i, 3) 34, 4)
|
Методические рекомендации по использованию на уроке:
|
Примеры можно использовать как тренировочные на каждое арифметическое действие на этапе актуализации знаний.
Рассчитаны на всех учащихся.
|
Тема:
|
Комплексные числа. Арифметические действия над комплексными числами
|
Цель обучения:
|
11.1.2.3 - уметь извлекать квадратный корень из комплексного числа;
|
Условие задачи:
|
(2i−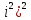 + (1−3i + (1−3i . .
|
Решение:
|
Решение.
(2i−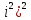 +(1−3i +(1−3i =(2i+1 =(2i+1 +1−3(3i +1−3(3i +3(3i)−(3i +3(3i)−(3i = =
=4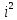 +4i+1−27 +4i+1−27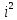 +9i−27 +9i−27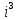 =−4+4i+1+27−9i+27i =−4+4i+1+27−9i+27i
=24+22i=24+22i.
|
Ответ:
|
24+22i
|
Методические рекомендации по использованию на уроке:
|
Задание для большинства.
|
Тема:
|
Арифметические действия над комплексными числами в алгебраической форме.
|
Цель обучения:
|
11.1.2.1. выпонять арифметические действия над комплексными числами в алгебраической форме.
|
Условие задачи:
|
Выполните умножение (2 + 3i) (5 – 7i).
Найти частное 
|
Решение:
|
1)
1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7)+ 3⋅ 5)i = (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) = 10 – 14i + 15i + 21 = 31 + i.
2)
1 способ.

2 способ.
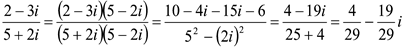
|
Ответ:
|
31 + i;
 - -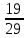 і. і.
|
Методические рекомендации по использованию на уроке:
|
Эти прмеры можно прорешать вместе с учащимися сразу после объяснения темы. Дать на самостоятельную работу 3-5 мин. После провести взаимопроверку в парах и решить у доски. Свериться с верным решением.
|
Тема:
|
Комплексная плоскость. Модуль комплексного числа
|
Цель обучения:
|
11.1.1.2 - уметь изображать комплексное число на комплексной плоскости
|
Условие задачи:
|
Комплексное число z=2+2i изобразить на плоскости и записать в тригонометрической форме:
|
Решение:
|
 
y

2
R=|z|=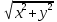 x=2, y=2 x=2, y=2

 R= R= =2√2 α =2√2 α
   
0
x
2
Для 1 четверти arg z= arctg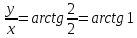
α=arg z = π/4
2+2i=2√2(cos π/4+i sin π/4)
|
Ответ:
|
2+2i=2√2(cos π/4+i sin π/4)
|
Методические рекомендации по использованию на уроке:
|
Задачу можно дать в качестве индивидуальной домашней работы или для работы в группе учащимся уровня А,В.
|
Тема:
|
Комплексная плоскость. Модуль комплексного числа.
|
Цель обучения:
|
11.1.1.1 - знать определение комплексного числа и его модуля;
|
Условие задачи:
|
Найти модуль комплексных чисел:
z1 = 4–3i и z2 = –2–2i.
|
Решение:
|
|z1|=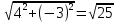 =5 =5
|z2|=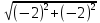 = =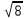 = =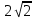
|
Ответ:
|
Z1=5
Z2=2
|
Методические рекомендации по использованию на уроке:
|
примеры для самостоятельного решения после объяснения материала
|
Тема:
|
Комплексные корни квадратного уравнения
|
Цель обучения:
|
11.1.2.4. решать квадратные уравнения на множестве комплексных чисел.
|
Условие задачи:
|
Составить квадратное уравнение, которое имеет корни z1=1−i и z2=4−5i. Решить его.
|
Решение:
|
Известно, что если z1, z2 - корни квадратного уравнения z2+bz+c=0, то указанное уравнение можно записать в виде (z−z1)(z−z2)=0. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:
(z−(1−i))(z−(4−5i))=0
Раскрываем скобки и выполняем операции над комплексными числами:
z2−(4−5i)z−(1−i)z+(1−i)(4−5i)=0
z2+z(−4+5i−1+i)+4−5i−4i+5i2=0
z2+(−5+6i)z−(1+9i)=0 - искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
D=(−5+6i)2−4⋅1⋅(−(1+9i))=−11−60i+4+36i=−7−24i
Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде√ D=a+bi. То есть
√−7−24i=a+bi⇒−7−24i=(a+bi)2⇒−7−24i=a2+2abi−b2
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений a и b:
a2−b2=−7
2ab=−24
решив которую, имеем, что a1=3, b1=−4 или a2=−3, b2=4. Рассматривая любую из полученных пар, например, первую, получаем, что√ D=3−4i, а тогда
z1= 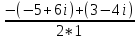 = 4−5i = 4−5i
z2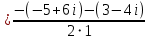 = 1−i = 1−i
Ответ. z2+(-5+6i)z-(1+9i)
|
Ответ:
|
z2+(-5+6i)z-(1+9i)
|
Методические рекомендации по использованию на уроке:
|
Эту работу можно предложить более сильным учащимся на этапе закрепления темы «Комплексные корни квадратного уравнения»
|
Тема:
|
Комплексные корни квадратного уравнения
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел
|
Условие задачи:
|
Решить уравнение .
|
Решение:
|
Вычислим дискриминант
.
Вычисляем корни из дискриминанта по формуле квадратных корней из комплексного числа: (можно вывести формулу решив систему)
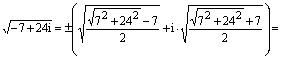
.
Вычисляем корни уравнения по формуле корней квадратного уравнения:
или
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать на уроках Проблемного обучения- дать в группах для решения учащимся уровня А,В. По результату сделать выводы и вывести формулу.
|
Тема:
|
Решение квадратных уравнений на множестве комплексных чисел. Основная теорема алгебры
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел
|
Условие задачи:
|
Решите уравнение:
|
Решение:
|
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным формулам получаем два корня:
– сопряженные комплексные корни
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Пример можно дать на первом уроке для наработки навыков решения уравнений.
| |
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.