оззиз. Методические укзания ОЗЗ_Часть 1-2. Методические указания для студентов к практическим занятиям по дисциплине общественное здоровье и здравоохранение
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
ТЕМА ЗАНЯТИЯ «СРЕДНИЕ ВЕЛИЧИНЫ В МЕДИЦИНСКОЙ СТАТИСТИКЕ» АКТУАЛЬНОСТЬ ТЕМЫ Средняя величина — это производная величина статистической совокупности, выражающая типичные размеры количественно варьирующего признака качественного однородного общественного явления. Средняя величина всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. Производная величина – это величина, которая в системе величин определена через основные величины. При исчислении средних величин в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Средние величины в медицинской статистике используются для оценки здоровья населения (средний рост, средняя масса тела, средняя окружность грудной клетки и др.), анализа деятельности медицинских организаций (средняя длительность пребывания больного в стационаре, средне число работы койки в году, среднее число посещений на одного врача и др.), результатов клинических исследований (средняя частота пульса, средние уровни содержания биохимических элементов в крови и др.), при характеристике среды обитания, санитарно-эпидемиологических условий (средняя жилая площадь на одного человека, среднее число кишечных палочек в 1 мл воды и др.). В статистике различают несколько десятков средних величин. В прикладной медицинской статистике обычно используются 3 вида средних величин: средняя арифметическая (М — Media), мода (Мо), медиана (Mе). Другие виды средних величин (средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая, средняя смешанная и др.) применяются в специальных экспериментальных углубленных исследованиях. Приведем пример, классификации, удобную для прикладной медицинской статистики, предложенную итальянским ученым К. Джини. По его классификации все средние величины делятся на две большие группы: а) средние аналитические; б) средние неаналитические. 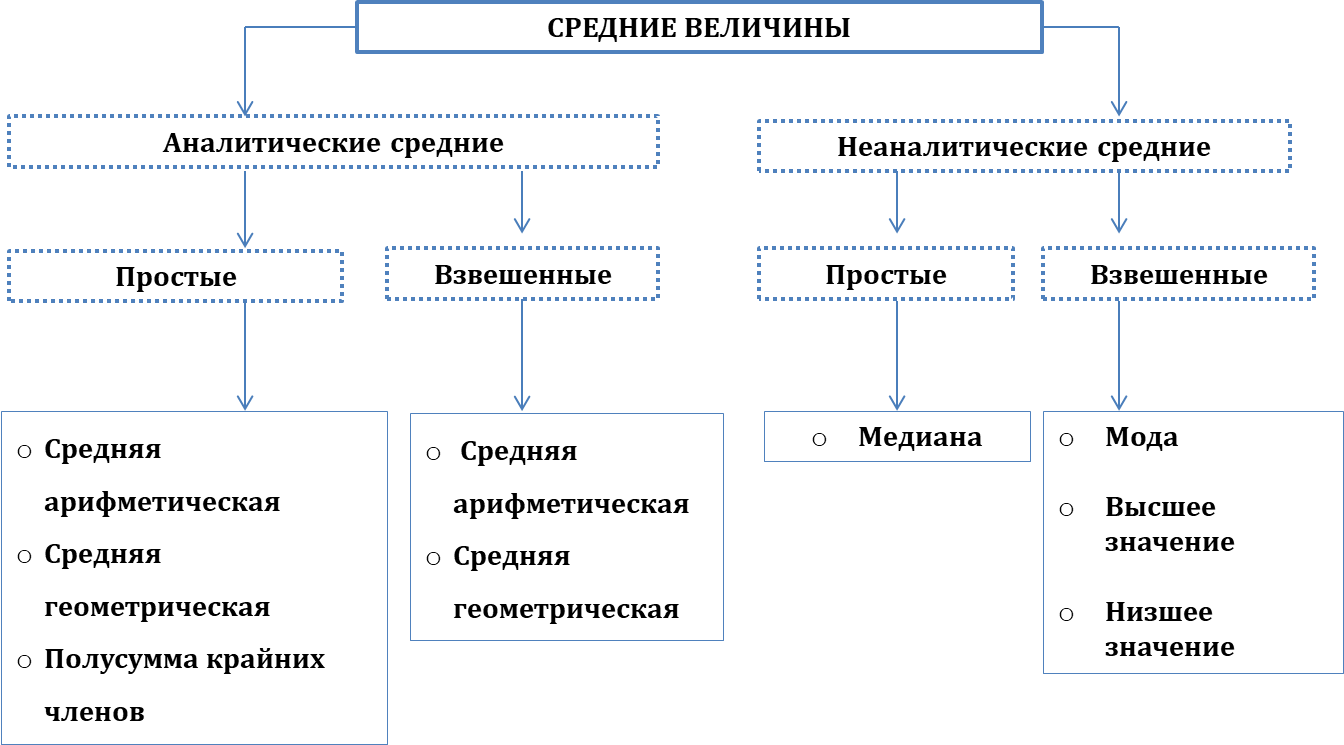 Рис. 1. Классификация средних величин (по К. Джини). Аналитические средние - это все средние величины, которые выражаются или определяются при помощи формул. Неаналитические средние (или позиционные) - определяются без формул. В свою очередь и те, и другие подразделяются на простые и взвешенные. Средние величины рассчитывают на основании вариационных рядов, достаточного числа наблюдений и однородных статистических групп. Вариационный ряд – это ряд чисел (вариант), характеризующих изучаемый признак, расположенных в ранговом порядке (в убывающей или возрастающей последовательности) с соответствующими этим вариантам (V) частотами (Р). Таблица № 1
Примеры вариационных рядов
Исследователям часто приходится работать с вариационными рядами, содержащими большое число вариант. Для облегчения техники вычисления средней арифметической величины объединяют варианты в группы и составляют так называемые сгруппированные вариационные ряды. При проведении группировки вариант необходимо соблюдать следующие условия. Каждая группа должна состоять из одинакового числа вариант. Полученной группе должна соответствовать частота, равная сумме частот вариант, вошедших в эту группу. Число вариант, входящих в группу не должно превышать 3-4. Все варианты вариационного ряда должны входить в группировки. Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили:
Составленные ряды вариационного ряда часто изображают графически, чтобы нагляднее представить особенности распределения. Наиболее распространёнными графиками являются гистограмма, кумулята, огива. 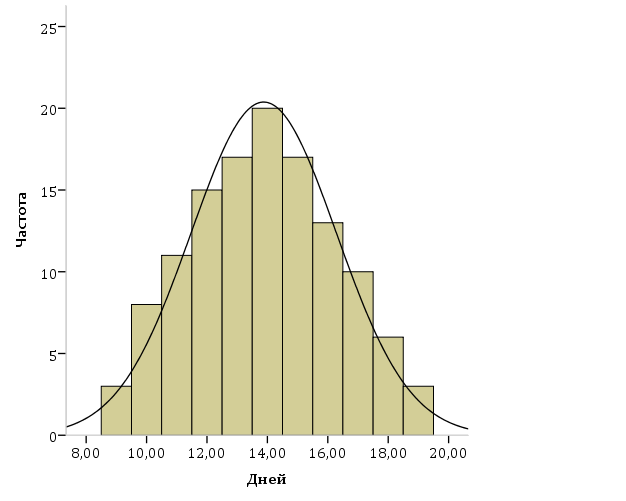 Рис .1. Гистограмма среднего числа дней лечения Основной целью анализа вариационных рядов является выявление закономерности распределения, исключая при этом влияние множество случайных для данного распределения факторов. Нормальное распределение признака наблюдается в тех случаях, когда на величину вариантов, входящих в состав вариационного ряда, действует множество случайных, независимых или слабо зависимых факторов, каждый из которых играет в общей сумме незначительную роль. Это следует из центральной предельной теоремы теории вероятностей. Нарушение нормального характера распределения часто является свидетельством неоднородности совокупности. Нормальное распределение (Гаусса-Лапласа) – это распределение, при котором переменная величина изменяется непрерывно, причем крайние значения величины (наибольшие и наименьшие) появляются редко, но чем ближе значения признака к центру (к средней арифметической), тем оно чаще встречается. Нормальный закон распределения во всех естественных науках имеет фундаментальное значение. 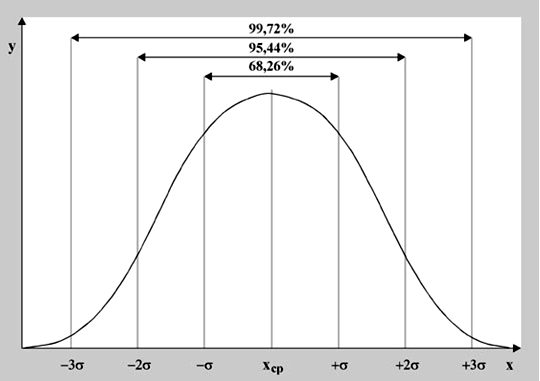 Рис.2 Кривая нормального распределения Гаусса-Лапласа. Кривая нормального распределения (кривая Гаусса-Лапласа, Гаусса-Ляпунова) - это теоретическая модель, колоколообразную фигуру, правая и левая ветви которой равномерно и симметрично убывают, асимптотически приближаясь к оси абсцисс. Отличительной особенностью этой кривой является совпадение в ней средней арифметической, моды и медианы. Ляпунов доказал, что если изучаемый признак представляет собой результат суммарного действия многих факторов, каждый из которых мало связан с большинством остальных, и влияние каждого фактора на конечный результат намного перекрывается суммарным влиянием всех остальных факторов, то распределение становится близким к нормальному распределению. Нормальное распределение зависит от двух параметров: μ (мю) — является математическим ожиданием (средним значением случайной величины), и σ ( сигма) — является стандартным отклонением (среднеквадратичным отклонением). Параметр μ определяет положение центра плотности вероятности нормального распределения, а σ — разброс относительно центра (среднего). Существует несколько способов определения того, является ли распределение нормальным (симметричным). Часто нормальность проверяется по правилу трех сигм. В условиях нормального распределения существует зависимость между величиной среднего квадратичного отклонения и количеством наблюдений: в пределах х±1о располагается 0,683, или 68,3%, количества наблюдений; в пределах х ± 2а располагается 0,954, или 95,4%, количества наблюдений; в пределах х ±3а — 0,997, или 99,7%, количества наблюдений. Если наблюдаемые значения признака отличаются от средней величины не более чем на За, то распределение считают нормальным. Часто характер асимметричности определяют по соотношению средней арифметической, медианы и моды. Для симметричного распределения эти величины совпадают. 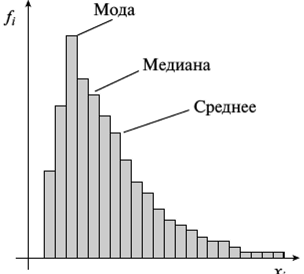 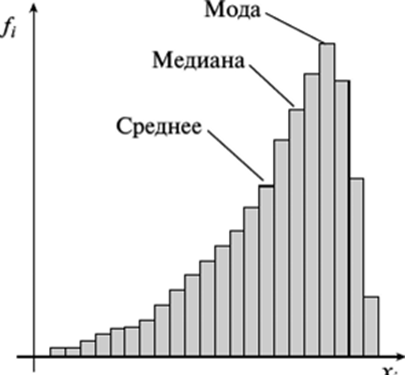 Рис. 3. Правосторонняя и левосторонняя асимметрия. При правосторонней асимметрии х > Ме> М0 распределение данных имеет вытянутую правую ветвь (рис.3 и 4). Средняя величина в этом случае может и не быть типической характеристикой изучаемой совокупности, так как на нее влияют несколько очень больших значений признака. При правосторонней асимметрии большинство единиц совокупности имеют значение признака, превышающее модальное значение. При левосторонней асимметрии х < Ме< М0 распределение данных имеет вытянутую левую ветвь (рис. 7.3). Средняя величина в этом случае также часто не является типической характеристикой изучаемой совокупности, так как на нее влияют несколько очень малых значений признака. При левосторонней асимметрии большинство единиц совокупности имеют значение признака меньше модального. Характер и степень асимметричности распределения можно определить с помощью специальных показателей — коэффициентов асимметрии и эксцесса распределения. Для нормального распределения эти характеристики равны нулю. Если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Моментный коэффициент асимметрии характеризует скошенность эмпирического (наблюдаемого) распределения влево или вправо относительно нормального распределения. Если As > О, то для распределения характерна правосторонняя асимметрия, если As <0 — левосторонняя асимметрия. При As > 0,5 асимметрия значительна. При исчислении моментного коэффициента асимметрии и его стандартной ошибки рекомендуется исключать из анализа резко отличающиеся единицы (выбросы). 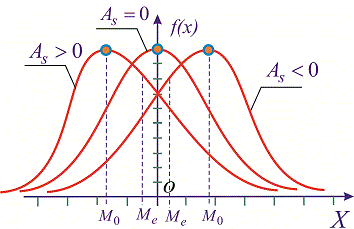 Рис. 4. Асимметрия кривой Гаусса-Лапласа Эксцесс — показатель, характеризующий плосковершинность или островершинность распределения. Он показывает отклонение вершины эмпирического распределения от вершины кривой нормального распределения вверх или вниз. Эксцесс рассчитывают только для симметричных распределений. Если Ех > 0, то распределение островершинное (рис. 7.4), если Ех < 0 — распределение плосковершинное. 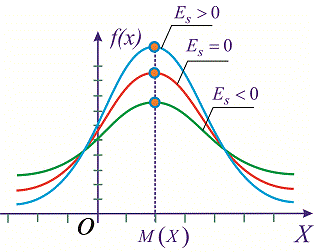 Рис.5. Эксцесс кривой Гаусса-Лапласа Описание (обобщение) количественного признака проводится по следующим этапам: 1) Определение вида распределения признака; 2) Оценка центральной тенденции изучаемой совокупности; 3) Оценка ее разнообразия (разброса). В случае распределения близкого к нормальному мы вправе для дальнейшего статистического анализа применять параметрическую статистику, если распределение отлично от нормального или при неизвестном распределении рекомендуется применять непараметрическую статистику. 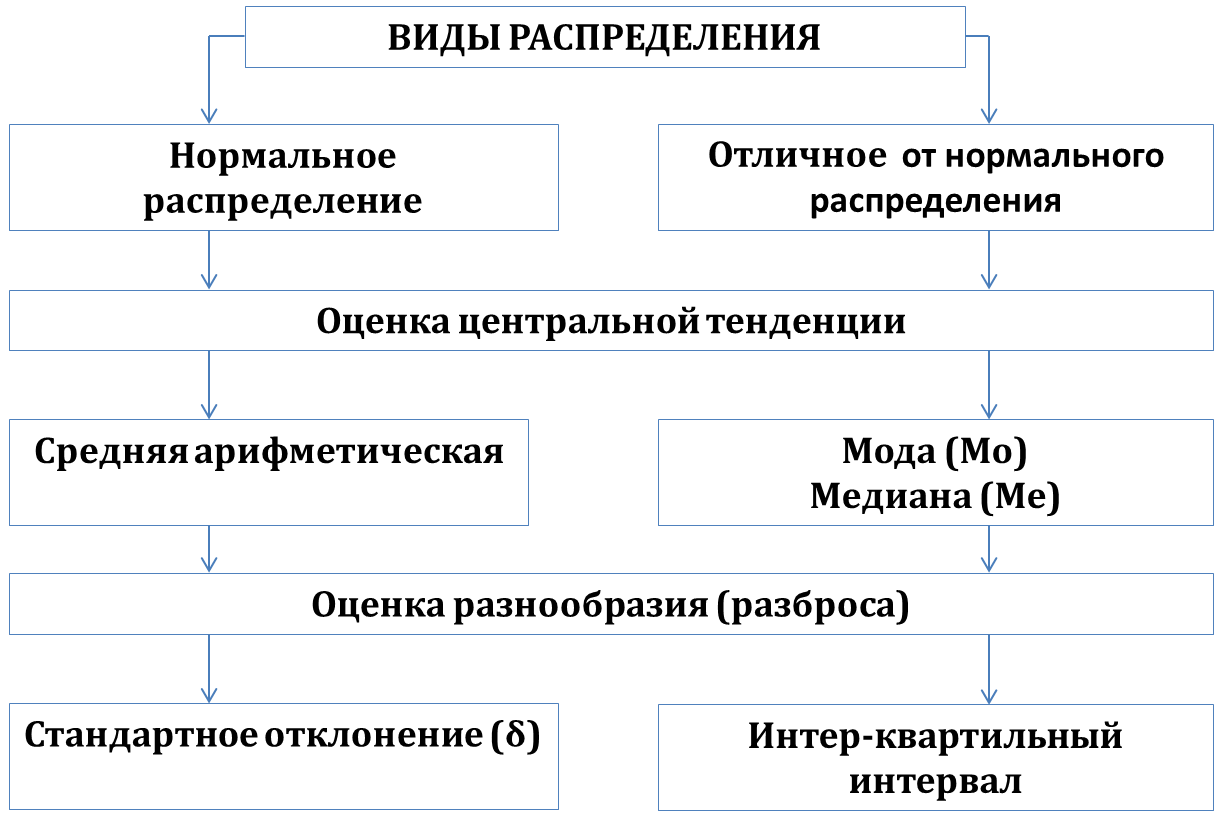 Рис. 6. Этапы описания (обобщения) количественного признака Непараметрические методы: не требуют предварительного знания вида распределения; не требуют предварительного расчета параметров распределения (средних величин, стандартного отклонения и др.); позволяют сравнивать совокупности с номинальными и порядковыми признаками; просты в применении. Отрицательные стороны непараметрических методов: обладают меньшей мощностью, чем параметрические методы; имеют существенные ограничения в применении по числу наблюдений. 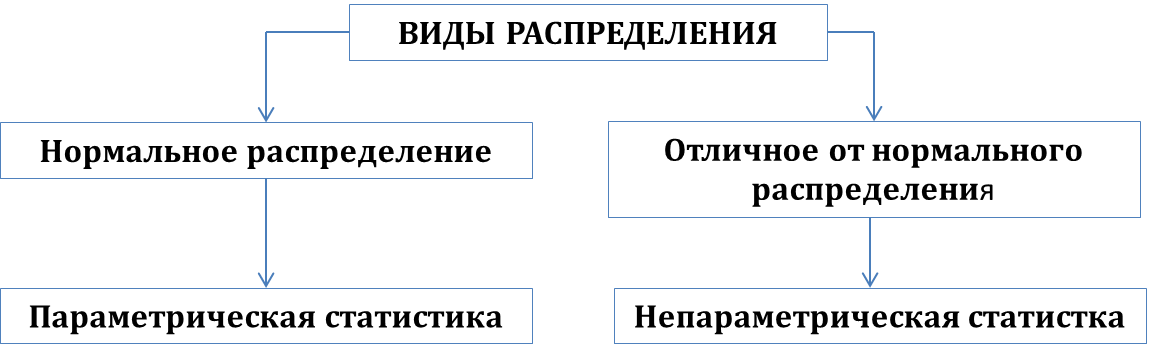 Рис. 6. Этапы описания (обобщения) количественного признака При асимметрии вариационного ряда в статистике широко используют структурные (неаналитические) средние величины. К их числу относятся непараметрические средние – мода и медиана. Также используют квартили, квинтили, децили, перцентили. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
