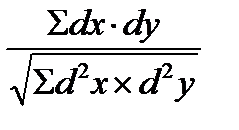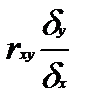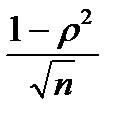оззиз. Методические укзания ОЗЗ_Часть 1-2. Методические указания для студентов к практическим занятиям по дисциплине общественное здоровье и здравоохранение
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
ТЕМА ЗАНЯТИЯ «ИЗМЕРЕНИЕ СВЯЗИ МЕЖДУ ИЗУЧАЕМЫМИ ЯВЛЕНИЯМИ» 1. АКТУАЛЬНОСТЬ ТЕМЫ Фундаментальным свойством всех процессов и явлений в природе и в обществе является их взаимозависимость. Выяснение наличия связей между изучаемыми явлениями (признаками) — одна из важных задач статистики. Определение взаимосвязи между явлениями в здравоохранении имеет большое значение. При анализе результатов медико-биологических и медико-социальных исследований часто возникает необходимость установления вида связи (зависимости) между величинами. Существует две категории зависимостей (функциональная и корреляционная) и две группы признаков (признаки-факторы и результативные признаки). Функциональные связи – это связи, при которых определенному значению одной переменной (признака-фактора) соответствует однозначно определяемое значение другой переменной (признака-результата). Функциональная зависимость предполагает, что уровень признака-результата полностью определяется величиной признака-фактора (факторов). Если между признаками установлена функциональная зависимость, то она справедлива для каждой единицы статистической совокупности. Чаще всего функциональные связи наблюдаются в явлениях, описываемых математикой, физикой и другими точными науками. Имеют место функциональные связи и в здравоохранении, но довольно редко (они отражают взаимосвязь только отдельных сторон сложных явлений в системе здравоохранения). Примером функциональной связи может служить связь между оплатой труда врача стоматолога и количеством поставленных коронок при простой сдельной оплате труда. В отличие от функциональной связи, где существует полное соответствие между факторными и результативными признаками, в корреляционной связи отсутствует это полное соответствие. Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Корреляционная связь проявляется только в средних величинах и выражает числовое отношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании или убывании другой. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков, неизвестно. Часто термины корреляционная связь и корреляционная зависимость используются как синонимы. Но зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Первым условием возможности изучения корреляционной связи как общее условие всякого статистического исследования является достаточное число наблюдений. Вторым условием закономерного проявления корреляционной связи служит условие, обеспечивающее надежное выражение закономерности в средней величине (нормальное ее распределение). Специальные статистические критерии для определения нормальности распределения были рассмотрены в теме «Средние величины». Корреляционная связь классифицируется по степени тесноты, направлению и аналитическому выражению. По направлению выделяют связь прямую и обратную. Прямая связь (положительная) - это такая связь, при которой с увеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) значений результативного. Обратная связь (отрицательная) – это такая связь, при котором значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака Таблица № 1 Оценка корреляционной связи по направлению
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные: Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида: у=а+bх. Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи. Если же связь может быть выражена уравнением какой-либо кривой линии (параболы, гиперболы и др.), то такую связь называют нелинейной (криволинейной) связью. Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака. Классификация связи по степени тесноты представлена в таблице 2. Таблица № 2 Таблица анализа силы связи между переменными (шкала Чеддока)
При отрицательной корреляционной связи значения силы связи между переменными меняют на противоположные. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Изучение корреляционных связей сводится в основном к решению следующих задач: выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками. измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов. Эта часть исследования называется корреляционный анализ; определение уравнения регрессии - математической модели, в которой среднее значение результативного признака рассматривается как функция одной или нескольких переменных - факторных признаков. Эта часть исследования называется регрессионный анализ. Задача корреляционного анализа - измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние. Задача регрессионного анализа - выбор типа модели (формы связи), устанавливающих степени влияния независимых переменных. Связь признаков проявляется в их согласованной вариации, при этом одни признаки выступают как факторные, а другие - как результативные. Причинно-следственная связь факторных и результативных признаков характеризуется по степени: тесноты; направлению; аналитическому выражению. Корреляционный анализ выполняет оценку адекватности регрессионной модели, путем установления тесноты связи. В корреляционном анализе используют следующие виды зависимостей: Парную корреляцию – связь между двумя признаками (результативным и факторным или двумя факторными). Частную корреляцию – зависимость между результативным и одним факторным признаком при фиксированных значениях других факторных признаков. Множественную корреляцию – зависимость между результативным и двумя и более факторными признаками. К простейшим показателям тесной связи в корреляционном анализе относят: линейный парный коэффициент корреляции К. Пирсона; коэффициент детерминации; коэффициенты корреляции знаков - для оценки тесноты связи качественных признаков (непараметрические методы), Г. Фехнера, К. Спирмена, М. Кэндэла. В практической работе мы остановимся на двух простых показателях оценки тесноты связи корреляционного анализа: 1) Коэффициент линейной парной корреляции Пирсона (параметрический метод); 2) Коэффициент ранговой корреляции Спирмена (непараметрический метод). Коэффициент линейной парной корреляции Пирсона (критерий корреляции Пирсона) Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. Данный коэффициент характеризует существование линейной связи между двумя величинами. Если связь криволинейная то коэффициент не будет работать. Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой - определяются при помощи регрессионного анализа. Чтобы приступать к расчетам коэффициента корреляции r-Пирсона необходимо выполнение следующих условий: Сопоставляемые показатели X и Y должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление). Исследуемые переменные X и Y должны быть распределены нормально. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым. Таблицы уровней значимости (достоверности) для коэффициента корреляции Пирсона рассчитаны от n = 5 до n = 1000. Оценка уровня значимости по таблицам осуществляется при числе степеней свободы v= n – 2. В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy. Коэффициента корреляции Пирсона рассчитывается по формуле: 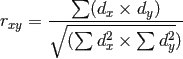 Методика и порядок вычисления коэффициента корреляции Пирсона: Построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно х и у; Определить для каждого вариационного ряда средние значения (М1 и М2); Найти отклонения (dх и dy) каждого числового значения от среднего значения своего вариационного ряда; Ролученные отклонения перемножить (dx X dy); Каждое отклонение возвести в квадрат и суммировать по каждому ряду (Σ dx2 и dy2); Подставить полученные значения в формулу расчета коэффициента корреляции. Интерпретация значения коэффициента корреляции Пирсона Значения коэффициента корреляции Пирсона интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение rxy – тем выше теснота связи между двумя величинами. rxy = 0 говорит о полном отсутствии связи. rxy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка. Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy < 0.3 свидетельствуют о слабой связи, значения rxy от 0.3 до 0.7 - о связи средней тесноты, значения rxy > 0.7 - о сильной связи. Более точную оценку силы корреляционной связи можно получить, если воспользоваться шкалу Чеддока. 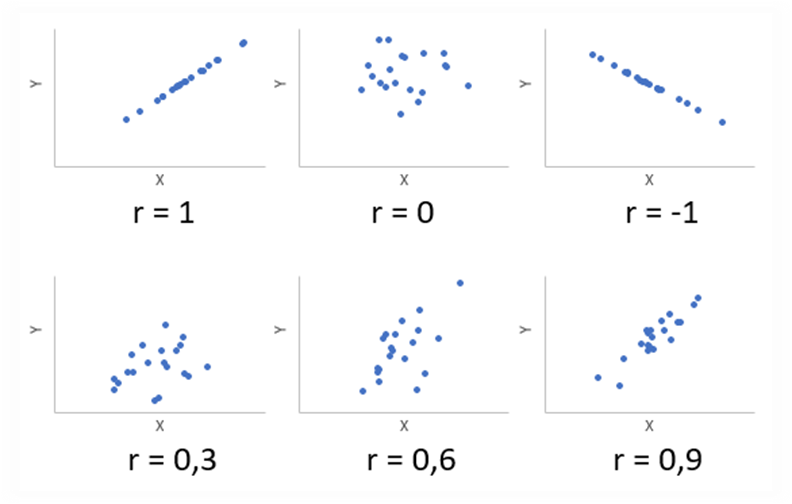 Рис. 1. Диаграммы рассеяния при некоторых значениях коэффициента корреляции Пирсона: (r=−1; r=0; r=-1; r=0,3; r=0,6; r=0,9). Расчет коэффициента корреляции Пирсона может ввести в заблуждение, если: Соотношение между двумя переменными нелинейное Данные включают более одного наблюдения по каждому случаю; Есть аномальные значения (выбросы); Данные содержат ярко выраженные подгруппы наблюдений. 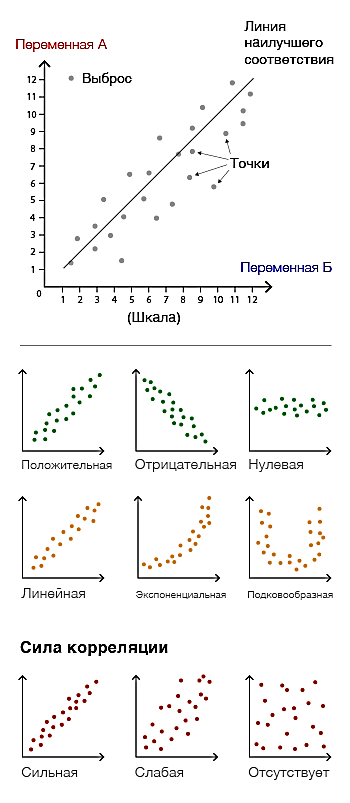 Рис.2. Аномальное значение (выброс). Коэффициент ранговой корреляции Спирмена (непараметрический метод). Ранговая корреляция – это метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. В случае, когда силу зависимости между случайными величинами невозможно определить численно при помощи обычного коэффициента корреляции, используют ранговую корреляцию, которая имеет дело не с непосредственными значениями, а с рангами (порядковыми номерами). Ранги - это порядковые номера единиц совокупности в ранжированном ряду. Если проранжировать совокупность по двум признакам, связь между которыми изучается, то полное совпадение рангов означает максимально тесную прямую связь, а полная противоположность рангов - максимально тесную обратную связь. Ранжировать оба признака необходимо в одном и том же порядке: либо от меньших значений признака к большим, либо наоборот. Для практических целей использование ранговой корреляции весьма полезно. Например, если установлена высокая ранговая корреляция между двумя качественными признаками, то достаточно контролировать только один из признаков, что удешевляет и ускоряет контроль. Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Ранговый коэффициент корреляции Спирмена подсчитывается по формуле: 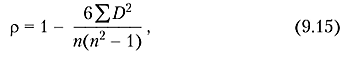 D- разность между рангами по двум переменным n – число сопоставляемых пар Методика и порядок вычисления коэффициента ранговой корреляции К. Спирмена: Составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют. Сопоставить каждому из значений признаков свой ранг (для одинаковых значений ранг вычисляется как среднее арифметическое рангов). Определить разность рангов между х и у (D): D = х — у Возвести полученную разность рангов в квадрат (D2) Получить сумму квадратов разности (Σ D2) и подставить полученные значения в формулу. Интерпретация значения коэффициента корреляции Спирмена производится также как и метод Пирсона по общепринятым методикам. При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи. Также для оценки тесноты связи может использоваться шкала Чеддока. Оценка статистической значимости коэффициентов корреляции Пирсона и Спиремена 1) Осуществляется при помощи t-критерия Стьюдента, рассчитываемого по следующей формуле: Полученное значение tr сравнивается с критическим значением (tкрит.) по таблицам Стюдента, при определенном уровне значимости и числе степеней свободы n-2, где n — число парных вариант. Если рассчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если рассчитанное значение t-критерия больше, то корреляционная связь считается статистически значимой. 2) Осуществляется при помощи вычисления средней ошибки коэффициента корреляции и расчета достоверности коэффициента корреляции При достаточно большом числе наблюдений (больше 100) средняя ошибка коэффициента корреляции вычисляется по формуле: В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:: С достаточной надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (rxy>=3mr). Обычно это отношение коэффициента корреляции (rху) к его средней ошибке (тr) обозначают буквой t и называют критерием достоверности Стьюдента: 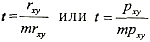 Если t ≥3, то коэффициент корреляции достоверен В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, т. е. для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции определяется по формуле: Достоверность коэффициента корреляции оценивают также по критерию t (Стьюдента) Значения эмпирического критерия t оцениваются по таблице t Стьюдента при числе степеней свободы v = п – 2, где n — число парных вариант. Если величина t больше табличного значения t 0,05, то коэффициент корреляции признается надежным с доверительной вероятностью больше 95%., различия считаются статистически значимыми. 2. УЧЕБНЫЕ ЦЕЛИ: Научить применять методики вычисления и анализа линейной парной корреляции Пирсона и ранговой корреляции Спирмена. ПО ОКОНЧАНИИ ИЗУЧЕНИЯ ТЕМЫ ПРАКТИЧЕСКОГО ЗАНЯТИЯ У СТУДЕНТА ДОЛЖНЫ БЫТЬ СФОРМИРОВАНЫ СЛЕДУЮЩИЕ КОМПЕТЕНЦИИ: ОК-1 способность к абстрактному мышлению, анализу, синтезу. ОПК-4 - способность и готовность реализовать этические и деонтологические принципы в профессиональной деятельности ПК-4 - способность и готовность к применению социально-гигиенических методик сбора и медико-статистического анализа информации о показателях здоровья населения ПК -20 - готовностью к анализу и публичному представлению медицинской информации на основе доказательной медицины ПК -21 - способностью к участию в проведении научных исследований ПК -22 - готовностью к участию во внедрении новых методов и методик, направленных на охрану здоровья граждан ДЛЯ ФОРМИРОВАНИЯ УКАЗАННЫХ КОМПЕТЕНЦИЙ СТУДЕНТ ДОЛЖЕН ЗНАТЬ: основные термины и понятия условия применения, методику расчета и оценку результатов параметрических методов оценки связи между явлениями (на примере критерия Пирсона) условия применения, методику расчета и оценку результатов непараметрических методов оценки связи между явлениями (на примере критерия Спирмена) УМЕТЬ: выбрать адекватный метод оценки связи рассчитать коэффициенты корреляции оценивать связь между явлениями, сделать вывод ВЛАДЕТЬ: методикой расчета параметрического метода корреляционного анализа Пирсона методикой расчета непараметрического метода корреляционного анализа Спирмена методиками оценка статистической значимости коэффициентов корреляции Пирсона и Спиремена 3. МАТЕРИАЛЫ ДЛЯ САМОПОДГОТОВКИ К ОСВОЕНИЮ ДАННОЙ ТЕМЫ: ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ: Дайте определение функциональной и корреляционной связи. Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками. В каких случаях применяется метод квадратов? В каких случаях применяется ранговый метод вычисления коэффициента корреляции? Каковы основные этапы вычисления коэффициента корреляции методом квадратов? Каковы основные этапы вычисления коэффициента корреляции методом ранговым методом? Укажите способы определения достоверности коэффициента корреляции. ВИД ЗАНЯТИЯ: практическое занятие ПРОДОЛЖИТЕЛЬНОСТЬ ЗАНЯТИЯ (В АКАДЕМИЧЕСКИХ ЧАСАХ): 4 часа 6. ОСНАЩЕНИЕ: 6.1.Дидактический материал (ситуационные задачи) 6.2. Технические средства обучения (ТСО) (компьютеры, мультимедийные проекторы) 7. СОДЕРЖАНИЕ ЗАНЯТИЯ: 7.1. КОНТРОЛЬ ИСХОДНОГО УРОВНЯ ЗНАНИЙ И УМЕНИЙ. Задания для самоконтроля: решение студентами индивидуальных наборов тестовых заданий по теме: Задание 1 При функциональной факторной зависимости между признаками каждому значению факторного признака соответствует; а) модальное значение результативного признака b) одно значение результативного признака c) нулевое значение результативного признака d) среднее значение результативного признака e) множество значений результативного признака 2. Корреляционная связь, при которой одни признак увеличивается, а второй уменьшается, оценивается как: а) прямая b) обратная c) сильная d) связь отсутствует e) связь полная 3. На наличие средней прямой линейной зависимости между признаками x и y указывает следующее значение коэффициента корреляции: а) 0,2 b) 0,4 c) 0,6 d) 0,8 e) 1,0 4. Корреляционный метод может быть применен, если число наблюдений больше: а) 5 b) 20 c) 30 d) 100 e) 400 5. Коэффициент корреляции по методу квадратов применяется при условии: а) когда нужны лишь ориентировочные данные о наличии связи b) когда ряды распределения взаимосвязанных признаков имеют открытые варианты c) когда ряды распределения имеют как количественное выражение, так и атрибутивные признаки d) когда ряды распределения имеют только атрибутивные признаки e) когда нужны точные данные о наличии связи 6.Укажите правильную формулу для расчета коэффициента ранговой корреляции:
7. Связь между признаками считается статистически значимой, если коэффициент корреляции превышает свою ошибку в: а) 1 раз b) 2 раза c) 3 раза d) 4 раза e) 5 раз 8. Как изменится ковариация двух переменных X и Y, если все значения обеих переменных вырастут в n раз: а) не изменится b) вырастет в n раз c) вырастет в 2n раз d) вырастет в 3n раз e) вырастет в n2 раз 9. Коэффициент Спирмена является показателем связи между переменными, измеренными в шкале: а) интервалов b) наименований c) рангов d) равных отношений e) последовательных значений 10. Коэффициент корреляции, равный «-0,3», свидетельствует: а) об отсутствии связи между явлениями b) о средней отрицательной связи между явлениями c) о слабой отрицательной связи между явлениями d) о сильной отрицательной связи между явлениями e) об очень слабой отрицательной связи между явлениями Задание 2 1. Функциональная связь характерна для процессов: а) медицинских b) социологических c) биологических d) политических e) физико-математических 2. Корреляционный анализ определяет: а) форму связи между X и Y b) производную Y'x c) тесноту связи между X и Y d) интеграл(xdx)+интеграл(ydy) e) производную х2+х 3. Коэффициент корреляции Пирсона является мерой: а) статистической связи между случайными величинами b) вероятностной связи между случайными величинами c) корреляционной связи между случайными величинами d) линейной связи между случайными величинами e) функциональной связи между случайными величинами 4. Коэффициент корреляции измеряется в: а) процентах b) промилле c) продецимилле d) тех же единицах, что и изучаемый признак e) не имеет единиц измерения 5. Для изучения связи, в которой присутствует более одной независимой переменной используется: а) парная корреляция b) частная корреляция c) множественная корреляция d) коэффициенты ранговой корреляции e) коэффициенты линейной корреляции 6. Коэффициент корреляции изменяется от а) -1 до 0 b) 1 до 0 c) -1 до + 1 d) -0,99 до + 0,99 e) -0,9 до 0,9 7. Условия для расчета коэффициента ранговой корреляции; а) для расчета используются несгруппированные ряды значений двух признаков b) расчет производится между качественными признаками c) расчет изменения величины одного признака при изменении величины другого признака на единицу d) достаточно ориентировочных данных об уровне признака e) расчет производится между количественными признаками 8. Коэффициент корреляции не превышает значения: а) 5,0 b) 0,5 c) 1,0 d) 2,0 e) 2,5 9. Мерой степени тесноты связи для нелинейной формы зависимости является: а) коэффициент множественной корреляции b) коэффициент корреляции рангов c) коэффициент парной корреляции d) коэффициент детерминации e) коэффициент регрессии 10. Вид уравнения, характеризующего корреляционную связь, можно обосновать с использованием а) корреляционного анализа b) индексного метода c) логического анализа d) регрессионного анализа e) рядов динамики Задание 3 1. Связь между признаками является функциональной, если значение линейного коэффициента корреляции равно: а) 0,0 b) 0,3 c) 0,7 d) 0,9 e) 1,0 2. Практическое использование корреляционного анализа: а) расчет обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков b) сравнение степени однородности исследуемых совокупностей c) определение пределов возможных колебаний совокупностей d) выявление взаимодействия факторов, определение силы и направления влияния одних факторов на другие e) выявление тенденции показателей 3. При корреляционной факторной связи каждому значению факторного признака соответствует: а) модальное значение результативного признака b) одно значение результативного признака c) нулевое значение результативного признака d) среднее значение результативного признака e) множество значений результативного признака 4. По направлению корреляционная связь классифицируется как: а) линейная b) прямая c) криволинейная d) зависимая e) функциональная 5. Для оценки степени тесноты связи при линейной зависимости используется: а) коэффициент множественной корреляции b) коэффициент корреляции рангов c) коэффициент парной корреляции d) коэффициент детерминации e) коэффициент регрессии 6. Условием корреляционного анализа является необходимость подчинения совокупности по результативному и факториальному признакам, закону: а) условного распределения b) нормальному закону распределения вероятностей c) распределению Пуассона d) геометрическому распределению e) биномиальному распределению 7. Связь между признаками считается статистически значимой, если величина коэффициента корреляции больше или равна табличной при: а) p = 0,1 b) p = 0,3 c) p = 0,5 d) p = 0,06 e) p = 0,05 8. Коэффициент корреляции рангов Спирмена можно применить для оценки тесноты связи между: а) количественными признаками b) качественными признаками, проявления (значения) которых можно упорядочить c) любыми качественными признаками d) атрибутивными признаками e) учетными признаками 9. Связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах, называется: а) функциональная b) корреляционная c) закономерная d) условная e) вероятностная Для расчета коэффициента корреляции Спирмена необходимо: а) расположить переменные в порядке возрастания b) расположить переменные в порядке убывания c) возвести переменные в квадрат d) определить для каждого ряда средние значения e) присвоить переменным в порядке возрастания последовательные ранги (номера 1, 2, 3, .., n) 7.2. РАЗБОР С ПРЕПОДАВАТЕЛЕМ КЛЮЧЕВЫХ ВОПРОСОВ, НЕОБХОДИМЫХ ДЛЯ ОСВОЕНИЯ ТЕМЫ ЗАНЯТИЯ. Дайте определение функциональной связи и приведите примеры? Дайте определение корреляционной связи и приведите примеры? Каковы основные свойства корреляционных связей? Что такое корреляционная зависимость? Дайте характеристику корреляционной связи по направлению, силе, форме? Приведите примеры прямой и обратной корреляционной связи? Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками? Дайте определение понятию «выбросы»? Что изучает корреляционный анализ? Что такое коэффициент корреляции? В каких случаях рекомендуется применять коэффициент корреляции Пирсона? Каковы основные этапы вычисления коэффициента корреляции Пирсона? В каких случаях рекомендуется применять коэффициент корреляции Спирмена? Каковы основные этапы вычисления коэффициента корреляции Спирмена? Что означает «значимость коэффициента корреляции»? Как проверить значимость коэффициента корреляции? 7.3. ДЕМОНСТРАЦИЯ ПРЕПОДАВАТЕЛЕМ МЕТОДИКИ ПРАКТИЧЕСКИХ ПРИЕМОВ ПО ДАННОЙ ТЕМЕ Преподавателем даются практические рекомендации студентам по применению методов вычисления линейного парного коэффициента корреляции Пирсона, рангового коэффициента корреляции Спирмена, статистической значимости коэффициентов корреляции Пирсона и Спиремена. 7.4. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ ПОД КОНТРОЛЕМ ПРЕПОДАВАТЕЛЯ Case-задание № 1. 1. При изучении физического развития десятилетних мальчиков были получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. 2. На одном из заводов у рабочих-котельщиков, имеющих разный стаж работы, было исследовано состояние слуха и получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития Case-задание № 2 При изучении физиологии сна при депрессии исследователь столкнулся с необходимостью оценивать тяжесть этого заболевания. С этой целью использовались шкала депрессии Бека и шкала депрессии Гамильтона. Сравнив оценки по обеим шкалам у 10 больных, исследователь получил следующие результаты.
Задание: Вычислить коэффициент корреляции оценочных шкал депрессии (метод Пирсона). Определить ошибку коэффициента корреляции и его достоверности. Дать оценку степени тесноты и характера связи между признаками развития. 2. Определить характер и степень тесноты связи между показателем выполнения плана периодических осмотров населения N-ого края и уровнем заболеваемости туберкулезом.
Задание: Вычислить коэффициент корреляции рангов (метод Спирмена). Определить ошибку коэффициента корреляции и его достоверности. Дать оценку степени тесноты и характера связи между признаками развития. Case-задание № 3 1. При изучении физического развития мальчиков в возрасте 15 лет были получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. 2. При определении количества бактерий в 1 мл воды и дозой хлора были получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента кор-реляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития Case-задание № 4 1. При изучении физического развития десятилетних мальчиков были получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития 2.При определении количества сцеженного молока у матерей разного возраста получены следующие данные:
Задание: 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. Case-задание № 5 1. При изучении зависимости уровня гнойничковых заболеваний и травм у рабочих предприятия, полученные следующие данные:
Задание: 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. 2.По результатам выборочного исследования установлены следующие данные о числе госпитализированных больных с сердечно-сосудистой недостаточностью в связи с возрастом:
Задание: 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. 7.5. КОНТРОЛЬ КОНЕЧНОГО УРОВНЯ УСВОЕНИЯ ТЕМЫ: Представьте качественную и количественную характеристику известных вам связей показателей медико-социальных явлений? Каково основное отличие корреляционной связи от других видов связей и какие задачи необходимо решить для ее определения? В чем заключается сущность известных вам статистических методов выявления наличия связи, ее характера и направления? Условия применения линейного парного коэффициента корреляции Пирсона Условия применения рангового коэффициента корреляции Спирмена Какая величина определяет достоверность коэффициента корреляции? УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ОБУЧАЮЩИХСЯ СТУДЕНТОВ ПО ДАННОЙ ТЕМЕ Провести выборочное обследование и изучить влияние возраста пациентов стационара на развитие сердечно-сосудистой патологии. Провести выборочное обследование и изучить влияние доступности медицинской помощи на развитие хронических заболеваний. Провести выборочное обследование и изучить влияние различных условий труда на здоровье работающих. Провести выборочное обследование и изучить влияние уровня образования на здоровье населения. Провести выборочное обследование и изучить влияние вредных факторов на здоровье несения. ЛИТЕРАТУРА (В Т.Ч. УКАЗАТЬ АДРЕСА ЭЛЕКТРОННЫХ РЕСУРСОВ): Основная: Общественное здоровье и здравоохранение : учебник для студентов медицинских вузов / Ю. П. Лисицын. - 2-е изд. - Москва : ГЭОТАР-Медиа, 2010. - 507 с. Общественное здоровье и здравоохранение: учебник для студентов высших учебных заведений / В. А. Медик, В. К. Юрьев. - 2-е изд., испр. и доп. - Москва : ГЭОТАР-Медиа, 2013. - 607 с. Общественное здоровье и здравоохранение: учебник для студентов / Н. И. Вишняков [и др.]. - 8-е изд., испр. и доп. - Москва : МЕДпресс-информ, 2016. - 832 с. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие: учебник для студентов медицинских вузов / [В. З. Кучеренко и др.]; под ред. В. З. Кучеренко. - 4-е изд., перераб. и доп. - Москва : ГЭОТАР-Медиа, 2011. - 245 с. Дополнительная: Общественное здоровье и здравоохранение: руководство к практическим занятиям ; учебное пособие для студентов высших учебных заведений / В. А. Медик, В. И. Лисицын, М. С. Токмачев. - Москва : ГЭОТАР-Медиа, 2013. - 394 с. Общественное здоровье и здравоохранение: (Учеб. для студентов, интернов, аспирантов, ординаторов педиатр. фак.) / В. К. Юрьев, Г. И. Куценко. - СПб. : Петрополис, 2000. - 910, [1] с. |