оззиз. Методические укзания ОЗЗ_Часть 1-2. Методические указания для студентов к практическим занятиям по дисциплине общественное здоровье и здравоохранение
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
Мода (Мо)– это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе соответствующей формулы. Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило, мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению. Медиана(Mе) – это значение признака, приходящееся на середину ранжированной совокупности. Иначе медиана – это величина, которая делит численность упорядоченного вариационного ряда на две равные части – одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие. Не важно, какого вариационного ряда дискретного или интервального. Для ранжированного ряда (т.е. упорядоченного - построенного в порядке возрастания или убывания индивидуальных значений признака) с нечетным числом членов (n=нечетное количество) медианой является варианта, расположенная в центре ряда. Порядковый номер медианы (NMe) определяется следующим образом: NMe=(n+1)/2. Для ранжированного ряда с четным числом членов (n=четное количество) – медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Порядковые номера двух центральных вариант определяются следующим образом:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану, так же как и моду, рассчитывают по определенному правилу. Медиана удобна тем, что на нее совершенно не оказывают влияние крайние члены ряда, и в таких случаях она даже более характерна, чем средняя, вычисленная для ряда в целом. Аналитические (степенные) средние величины относятся к разновидности средних величин и рассчитываются с помощью формул. Для вычисления аналитических средних величин необходимо использовать все имеющиеся значения признака. Наиболее распространенными в практике статистического анализа степенными средними являются: средняя арифметическая; средняя гармоническая, средняя геометрическая и средняя квадратическая. Степенные средние величины объединяются в общей формуле степенной средней при различной величине K. Если рассчитывать все виды степенных средних для одних и тех же данных, то их значения окажутся одинаковыми. Тогда действует правило мажорантности средних: с увеличением показателя степени средних увеличивается и сама средняя величина. Аналитические средние величины в зависимости от представления исходных данных могут быть простыми и взвешенными. Простые средние обычно рассчитываются, если исходная информация представлена в несгруппированном виде (в виде первичных данных). Взвешенные средние применяются в условиях наличия сгруппированных данных. Одной из наиболее распространённых в практике медико-социального анализа является средняя арифметическая величина. Её широкое использование определено возможностью определения общей величины признака путём простого суммирования отдельных значений. В общем виде значение средней определяется как отношение общего значения признака к объёму совокупности. Средняя арифметическая простая величина равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений. Она применяется в тех случаях, когда имеются не сгруппированные индивидуальные значения признака.
где М - средняя арифметическая, - сумма вариант, n - число наблюдений, V - варианты. Средняя арифметическая взвешенная - это средняя их вариант, которые повторяются различное число раз или имеют различный вес.
где М - средняя арифметическая; V – варианты; Р – частота; n - число всех наблюдений; Σ - знак суммирования. Основные свойства средней арифметической величины: Каждая варианта отклоняется от средней в большую или меньшую сторо-ну со знаком (+) или (–). Отклонение (d) определяется по формуле d = V – M. Сумма отклонений индивидуальных значений признака (вариант) от его среднего значения равна нулю. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число. Средняя арифметическая равна любой произвольно взятой варианте вариационного ряда плюс среднее отклонение этой варианты от всех вариант ряда. Среднее отклонение вариант условной средней имеет выражение
и называется моментом первой степени. Основываясь на этом свойстве, можно применить упрощенный способ вычисления средней арифметической (по способу моментов) пользуясь формулой:
где М - средняя арифметическая; М1 - условная средняя арифметическая; d - отклонение условной средней от варианты; Р – частота; Σ - знак суммирования. Для вычисления средней арифметической по способу моментов одну из вариант принимают за условную среднюю арифметическую (М1). Затем определяют отклонение (d) условной средней арифметической от вариант ряда (d = V - М1), умножив отклонение на частоту данной варианты получаем произведение: d×P. Суммировав произведение для всех вариант вариационного, получаем сумму произведений частот на отклонение, которое и подставляем в формулу. Пример вычисления средней арифметической по способу моментов: Возьмем ряд, который мы упростили. За условную среднюю примем варианту 34.
Параметры средней арифметической Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого она была вычислена. Средние величины являются важными характеристиками совокупности, однако они полностью не раскрывают индивидуальные значения признака, которые отличаются от средних и различаются между собой. Вокруг средней арифметической рассеяны различные варианты, поэтому понятно, что чем ближе друг к другу отдельные варианты по своей количественной характеристике, тем меньше рассеяние, колеблемость ряда, тем типичнее средняя арифметическая. Для оценки отклонения и разброса измеряемой средней величины пользуются несколькими различными критериями. В теории вероятностей и статистике к наиболее распространённому показателю рассеивания значений случайной величины относительно её математического ожидания относится – среднеквадратическое отклонение (среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс). При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок. Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. При определении среднего квадратического отклонения средней арифметической при достаточно большом объеме изучаемой совокупности (n > 30) применяется формула:
При расчете среднего квадратического отклонения по способу моментов используется формула: d - отклонение от средней арифметической. Таким образом, среднее квадратическое отклонение равно корню квадратному из разности момента второй степени и квадрата момента второй степени. Количественная репрезентативность достигается при использовании достаточного числа наблюдений в выборке, которое может обеспечить получение достоверных результатов. Качественная репрезентативность заключается в одинаковой структуре выборочной и генеральной совокупностей по признакам, имеющим влияние на получение конечного результата. Среднее квадратическое отклонение, является основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности. «Правило трех сигм» основанное на законе нормального распределения было описано ранее. Полученная средняя арифметическая (М) при повторных исследованиях под влиянием случайных явлений может изменяться на ту или иную величину. Мерой такой изменчивости служит средняя ошибка средней арифметической (m), которая определяется по формуле: 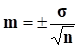 Средняя ошибка средней арифметической прямо пропорциональна средней колеблемости ряда и обратно пропорциональна числу наблюдений. При малом числе наблюдений (менее 30 случаев, так называемая малая выборка) средняя ошибка определяется по формуле 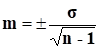 Установлено, что полученный средний результат при повторных наблюдениях, даже при одинаковых условиях, будет, в силу случайных колебаний отличаться от предыдущего результата. Теорией статистики установлена степень вероятности, с которой можно ожидать, что эти колебания не выйдут за пределы доверительного интервала М±t×m. В научно-исследовательской практике, с целью выявления, например, преимущества одного метода лечения перед другим, часто бывает необходимо провести сравнение средних величин. Для оценки достоверности разности двух средних величин пользуется формула Стьюдента, (применятся при нормальном распределении): где М1 и М2 - сравниваемые средние величины, m1 и m2 - средние ошибки средних величин. Разность считается достоверной, если число наблюдений, из которого определены средние величины, больше 100, то значение формулы должно быть не менее 2,6; если число наблюдений меньше чем 100, но больше 30, значение формулы должно быть не менее 3; если число наблюдений меньше 30, то достоверность разности двух средних величин определяется по таблице Стьюдента. Кроме рассмотренных выше величин, характеризующих вариационный ряд (М, σ, m), в статистике существует величина, которая также, как и среднее квадратическое отклонение, характеризует колеблемость вариационного ряда. Эта величина носит название коэффициента вариации. Коэффициент вариации применяется также и в том случае, если необходимо сравнивать колеблемость двух вариационных рядов выраженных в одинаковых единицах измерения, но средние арифметические этих рядов отличаются друг от друга на большую величину. Расчет коэффициента осуществляется по формуле В статистике принято, что: если коэффициент вариации меньше 10%, то степень рассеивания данных считается слабой; если от 10% до 20% - средней; больше 20% и меньше или равно 33% - сильной. Если значение коэффициента вариации не превышает 33%, то совокупность считается однородной, а если больше 33%, то – неоднородной. Оценка физического развития по методу сигмальных отклонений По методу сигмальных отклонений оцениваются соматометрические признаки - рост, масса тела, окружность грудной клетки. Метод сигмальных отклонений является наиболее простым. В этом случае показатели физического развития индивидуума сравнивают со средними арифметическими соответствующих возрастно-половых групп, взятыми из таблицы стандартов. При этом нужно из фактических данных роста, массы тела и окружности грудной клетки вычесть соответствующие показатели стандартов и полученную разность разделить на величину нормального отклонения признака от средней величины - сигму.
По величине сигмальных отклонений судят о степени физического развития. Отклонение размеров признака конкретного лица от средней величины признака лиц соответствующего возраста (совокупности) оценивается следующим образом: от - 1 σ до + 1 σ - среднее развитие от - 1 σ до - 2 σ - развитие ниже среднего от - 2 σ и меньше - низкое развитие от + 1 σ до + 2 σ - развитие выше среднего от + 2 σ и больше - высокое развитие Для комплексной оценки физического развития используются статистические методики, описанные в специальной литературе. 2. УЧЕБНЫЕ ЦЕЛИ: Научить применять методику вычисления и анализа средних величин и мер рассеяния для оценки явлений, связанных с общественным здоровьем и здравоохранением |
