Множества. Правила и действия над множествами
 Скачать 185.66 Kb.
|
Фундаментальная последовательность. Критерий Коши.Последовательность называется фундаментальной, если ∀ E>0, ∃ N ∀ n, m >N: |xn – xm| < E Критерий Коши: для того, чтобы последовательность сходилась необходимо и достаточно, чтобы она была фундаментальной. Доказательство (необходимость): xn →a: 1. ∀ E>0 ∃ N1 ∀ n⩾N1: | xn – a|<E/2 2. n=m: |xm - a| < E/2 |xn – xm| = |xn – a + a – xm| ⩽ |xn – a| +| xm – a |< E/2 + E/2 = E ⇒ |xn – xm|< E (достаточность): |xn – xm|< E ⇒ xm – E < xn< xm + E, ∃ m ⩾n0 ⇒ xn0 – E < xn< xn0 + E ⇒ xn – ограниченная последовательность, по теореме Б-В можно выделить сходящуюся подпоследовательность xnk : |xn – a|= |xn – xnk + xnk – a|⩽ ⩽ |xn – xnk | +| xnk – a|< E/2 + E/2 = E ⇒ |xn – a| Число Непера.xn = (1 + 1/n)n является сходящейся и называется числом Непера. Для того, что бы доказать, что данная последовательность сходящаяся нужно доказать, что: 1. Последовательность возрастает 2. Ограничена сверху некоторым числом 1. Для доказательства воспользуемся формулой бинома Ньютона: 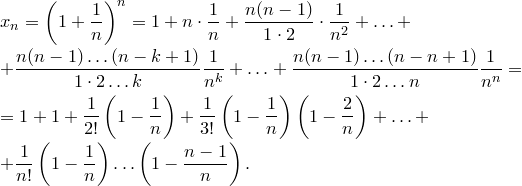 Если от  перейти к  , т.е. увеличить  на единицу, то, прежде всего, добавится новый,  -й полложительный член, каждый же из написанных  членов увеличится, так как любой множитель в скобках вида  заменится большим множителем  . Отсюда и следует, что  , т.е. последовательность  возрастает. 2.Покажем, что она ограничена сверху. Опустив в выражении для все множители в скобках, мы этим увеличим его, так чтоЗаменив каждый множитель в знаменателях дробей числом 2, мы еще увеличим полученное выражение:  Но прогрессия, начинающаяся членом 1/2, имеет сумму меньше 1, поэтому  . ЧТД |