Сравнение бесконечно малых. Примеры.
1. Если lim α(x)/β(x) = 1, α(x)
β(x)
2. lim α(x)/β(x) = A!=0, α(x) и β(x) имеют одинаковый порядок малости
3. lim α(x)/β(x) = 0, α(x) – имеет больший порядок малости
4. lim α(x)/β(x) = ∞, β(x) – имеет больший порядок малости
Первый замечательный предел.
lim sinx/x = 1, x→0
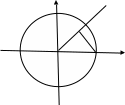 1. x → 0+0, x измеряется в радианах, 0
C
B
O A
 S OBA < Sкр.сектораOBA < SOCA (взята окружность произвольного радиуса r, с центром в начале координат)
½*r*r*sinx < ½*r2*x < ½*r*r*tgx (OA=x; AC=r*tgx) |: ½ r2
sinx 0
1
cosx
lim cosx = 1, x → 0+0 ⇒ lim sinx/x = 1, x → 0, согласно свойство о сжимающихся функциях
2. x → 0-0 ⇒ lim sinx/x = 1, x → 0 ЧТД
Второй замечательный предел.
lim (1 + 1/x)x = e, x →∞
Доказательство (на основе определения по Гейне):
Возьмём xn →+∞, n→∞ kn=E(xn) – целая часть ⇒ kn ⩽ xn ⩽ kn+1 (5)
1/(kn+1) ⩽ 1/xn ⩽ 1/kn(6)
1 + 1/(kn+1) ⩽ 1 + 1/xn ⩽ 1 + 1/kn (7)
(1 + 1/(kn+1))kn ⩽ (1 + 1/xn)xn ⩽ (1 + 1/kn)kn+1 (7)(5)
В последнем неравенстве переходим к пределу при xn →+∞, kn →+∞
lim (1 + 1/(kn+1))kn = lim (1 + 1/(kn+1))kn+1-1 = lim (1 + 1/(kn+1))kn+1 * lim (1 + 1/(kn+1))-1 = e
lim (1 + 1/kn)kn+1 = lim (1 + 1/kn)kn * lim (1 + 1/kn) = e*1 = e
Переходя к пределу получим: e ⩽ (1 + 1/xn)xn ⩽ e ⇒ lim (1 + 1/xn)xn = e, т.к. xn →+∞ выбиралось произвольно, то рассматривая случай xn →-∞, получим такой же результат, объединяя 2 случая lim (1 + 1/xn)xn = e ЧТД
|
Скачать 185.66 Kb.