Множества. Правила и действия над множествами
 Скачать 185.66 Kb.
|
Теорема об остатке формулы Тейлора в форме Пиано.Пусть функция дифференцируема и разложена в точке x0, тогда существует эпсилон окрестность точки x0 такая, что для любого х принадлежащего этой окрестности Rn= 0(x - x0)n. Доказательство: Т.к. функция дифференцирована n раз в точке x0, то это означает существование эпсилон окрестность точки x0, в которой определены f(x), а так же производная до n-1 ого порядка включительно, т.е. нам нужно доказать, что Rn(x)/(x – x0)n→0, при х→0 f(x) = f(x0) + f’(x0) (x – x0) + f’’(x0)/2! (x – x0)2 + f’’’(x0)/3! (x – x0)3 + … + f(n)(x0)/n! (x – x0)n + Rn , следовательно f(x) - f(x0) - f’(x0) (x – x0) - f’’(x0)/2! (x – x0)2 - f’’’(x0)/3! (x – x0)3 - … - f(n)(x0)/n! (x – x0)n = Rn [f(x) - f(x0) - f’(x0) (x – x0) - f’’(x0)/2! (x – x0)2 - f’’’(x0)/3! (x – x0)3 - … - f(n)(x0)/n! (x – x0)n]/ (x – x0)n →0 к этому выражению применяем 2ое правило Лопиталя, 1ое не применяем, т.к. g(x) будет равно 0 при х=0 1) [f’(x) – f’(x0) - f’’(x0) (x – x0) - f’’’(x0)/2! (x – x0)2 - … - f(n)(x0)/(n – 1)! (x – x0)n-1]/ n(x – x0)n-1 = 2) = [f’’(x) – f’’(x0) - f’’’(x0) (x – x0) – f(4)(x0)/2! (x – x0)2 - … - f(n)(x0)/(n – 2)! (x – x0)n-2]/ n(x – x0)n-2 = n-1) = [f(n-1)(x) – f(n)(x) (x – x0)]/ n!(x – x0) = на n-ом шаге у нас получится = [f(n)(x0) - f(n)(x0)]/n! = 0 (1ое правило Лопиталя) ЧТД Теоремы о достаточных условиях строгого экстремума.Пусть функциях y=f(x) определена хотя бы в некоторой окрестности т. х0 и существует первая производная f'(x0), тогда существует х0, которая называется точкой выпуклости (вогнутости) графика функции f(x), если найдётся такая Uδ (x0): ∀ x ∈ Uδ (x0) f(x)> f(x0) + f'(x0)(x – x0) – точка выпуклости ∀ x ∈ Uδ (x0) f(x)Б f(x0) + f'(x0)(x – x0) – точка вогнутости ⇓ не из лекций Теорема (первое достаточное условие экстремума в терминах первой производной)Пусть функция f(x) определена и дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой точки x0 и непрерывна в этой точке. Тогда: Если производная меняет знак с “-” на “+” при переходе через точку x0:∀x ∈ (x0 –δ;x0) f'(x) <0 и :∀x ∈ (x0 –δ;x0) (x0) f'(x) >0, то x0 – точка строго минимума функции Если производная  меняет знак с “+” на “-” при переходе через точку x0:∀x ∈ (x0 –δ;x0) f'(x) >0 и :∀x ∈ (x0 –δ;x0) (x0) f'(x) <0, то x0 – точка строго максимума функцииДоказательствоПусть, например, меняет знак с “-” на “+”. Рассмотрим точку x0 на сегменте  Воспользуемся теоремой о конечных приращениях Лагранжа:   ,  . Поскольку при переходе через точку x0 функция меняет знак с “-” на “+”, то  и  , то   Аналогично рассмотрим сегмент  , получим   x0 – точка строгого минимума функции.Замечания:Если x0 – точка строго экстремума, то из этого не следует, что производная меняет знак при переходе через точку x0 Теорема (второе достаточное условие строгого экстремума в терминах второй производной)Пусть дана функция f(x), она определена в некоторой окрестности точки x0, ее первая производная  и пусть  , тогда:Если  , то точка x0 – точка строгого минимума;Если  , то точка x0 – точка строгого максимума.ДоказательствоДокажем теорему для первого случая, когда 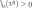. По скольку f''(x0) непрерывна, то на достаточно малом интервале  , т.к , то f'(x0) возрастает в этом интервале. , значит  на интервале  и  на интервале  .Таким образом функция f(x) убывает на интервале и возрастает на интервале по первому достаточному условию экстремума функция в точке x0 имеет минимум.Аналогично доказывается второй случай теоремы. Замечания:Если  и  , то функция f(x) может и не иметь экстремум в точке x0Теоремы о достаточных условиях точки перегиба.Пусть функциях y=f(x) имеет n производных в т. х0, кроме этого выполняется условие f'(x0)= f''(x0)= f(n-1)(x0)=0, f(n)(x0) ≠0. Тогда: если n – четное, n-ая производная> 0, х0 – точка строгой выпуклости если n – четное, n-ая производная< 0, х0 – точка строгой вогнутости если n – нечётное, то х0 – точка перегиба Доказательство: f(x) = f(x0) + f’(x0) (x – x0) + f’’(x0)/2! (x – x0)2 + f’’’(x0)/3! (x – x0)3 + … + f(n)(x0)/n! (x – x0)n + 0(x – x0)n f(x) - f(x0) - f’(x0) (x – x0) = (x – x0)n [f(n)(x0)/n! + 0(x – x0)n/ (x – x0)n] f(n)(x0) > 0, любого х принадлежащего эпсилон окрестность точки x0: 0(x – x0)n/ (x – x0)n < f(n)(x0)/n!, следовательно f(x) - f(x0) - f’(x0) (x – x0) > 0, следовательно по определению, x0 – точка выпуклости f(n)(x0) < 0, любого х принадлежащего эпсилон окрестность точки x0: 0(x – x0)n/ (x – x0)n > f(n)(x0)/n!, следовательно f(x) - f(x0) - f’(x0) (x – x0) < 0, следовательно по определению, x0 – точка вогнутости x ∈ (x0 – δ, x0): f(x) - f(x0) - f’(x0) (x – x0) < 0 x ∈ (x0, x0 + δ): f(x) - f(x0) - f’(x0) (x – x0) > 0 (при условии, что [ ] (+) ), следовательно x0 – точка перегиба ЧТД Схема исследования графика функции.Область определения функции Свойства функции a. четность f(-x)=f(x) – график функции симметричен относительно oy b. нечетность f(-x)=-f(x) – график функции симметричен относительно ox c. периодичность f(x+T)=f(x) – как правило указывает основной период Те точки разрыва, которые получаются в п1 исследуются в этом пункте, как правило бывает для одной точки два предела (предел слева, предел справа), однако бывают исключения, когда для одной точки исследуется только один предел; если в п1 разрывов нет, то п3 не исследуется Нахождние точек пересечения с осями (если они есть) Нахождение точек экстремума, возрастания и убывания, наибольшего и наименьшего значения Нахождение промежутков выпуклости, вогнутости и точек перегиба
Асимптоты вертикальные: lim f(x) = ±∞, x→ x0, если в п1 есть точки разрыва, то скорее всего через эти точки проходит вертикальная асимптота, x0- т. разрыва, особая точка, х = x0- вертикальная асимптота горизонтальные: lim f(x) = A, x→∞, y=A – горизонтальная асимптота наклонные: k=lim f(x)/x, x→∞, если в результате вычислений k = 0 или k =∞, то наклонных асимптот нет, b= lim (f(x) – kx), x→∞, y=kx + b – наклонная асимптота |
